
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вихідні дані до задач
|
|
|
|
| Варіант | Задача | ||||||||||||
| N | n | m | k | P1 | P2 | P1 | P2 | P3 | P4 | P | n | k | |
| 0.75 | 0.85 | 0.6 | 0.4 | 0.95 | 0.98 | 0.1 | |||||||
| 0.55 | 0.45 | 0.55 | 0.45 | 0.8 | 0.7 | 0.2 | |||||||
| 0.6 | 0.7 | 0.65 | 0.35 | 0.96 | 0.9 | 0.25 | |||||||
| 0.85 | 0.65 | 0.75 | 0.25 | 0.75 | 0.7 | 0.3 | |||||||
| 0.65 | 0.95 | 0.56 | 0.44 | 0.85 | 0.8 | 0.2 | |||||||
| 0.9 | 0.8 | 0.7 | 0.3 | 0.8 | 0.9 | 0.3 | |||||||
| 0.7 | 0.75 | 0.52 | 0.48 | 0.85 | 0.7 | 0.5 | |||||||
| 0.75 | 0.8 | 0.35 | 0.65 | 0.8 | 0.95 | 0.3 | |||||||
| 0.85 | 0.95 | 0.33 | 0.67 | 0.55 | 0.6 | 0.1 | |||||||
| 0.75 | 0.9 | 0.34 | 0.66 | 0.65 | 0.7 | 0.2 | |||||||
| 0.45 | 0.65 | 0.51 | 0.49 | 0.85 | 0.75 | 0.4 | |||||||
| 0.95 | 0.9 | 0.54 | 0.46 | 0.95 | 0.85 | 0.3 | |||||||
| 0.6 | 0.5 | 0.47 | 0.53 | 0.92 | 0.83 | 0.25 | |||||||
| 0.65 | 0.75 | 0.39 | 0.61 | 0.75 | 0.77 | 0.15 | |||||||
| 0.75 | 0.95 | 0.38 | 0.62 | 0.94 | 0.8 | 0.1 | |||||||
| 0.55 | 0.6 | 0.37 | 0.63 | 0.92 | 0.9 | 0.2 | |||||||
| 0.65 | 0.7 | 0.47 | 0.53 | 0.82 | 0.8 | 0.3 | |||||||
| 0.65 | 0.6 | 0.7 | 0.3 | 0.85 | 0.78 | 0.35 | |||||||
| 0.85 | 0.8 | 0.71 | 0.29 | 0.59 | 0.65 | 0.4 | |||||||
| 0.35 | 0.45 | 0.72 | 0.28 | 0.67 | 0.7 | 0.45 | |||||||
| 0.55 | 0.65 | 0.73 | 0.27 | 0.55 | 0.7 | 0.25 | |||||||
| 0.8 | 0.6 | 0.74 | 0.26 | 0.65 | 0.75 | 0.1 | |||||||
| 0.7 | 0.55 | 0.75 | 0.25 | 0.75 | 0.9 | 0.15 | |||||||
| 0.9 | 0.75 | 0.76 | 0.24 | 0.84 | 0.8 | 0.2 | |||||||
| 0.8 | 0.65 | 0.77 | 0.23 | 0.9 | 0.95 | 0.4 |
| Варіант | Задача | ||||||||||
| P | n | a | a | s | X1 | X2 | d | n | 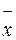
| d | |
Розв’язування типових прикладів
Завдання 1.
Ящик з N однаковими виробами містить n бракованих. Випадково відібрані m виробів і відправлені в магазин. Знайти ймовірність того, що серед них рівно k бракованих.
Розв’язок.
Загальне число можливих елементарних випадків дорівнює числу способів, яки можна вибрати m виробів з N, тобто дорівнює C  - числу комбінацій з N елементів по m.
- числу комбінацій з N елементів по m.
Число випадків,що сприяють появі події: серед m виробів рівно k бракованих; причому k бракованих виробів можна вибрати з n бракованих виробів С  способами; при цьому інші m – k виробів повинні бути не бракованими, котрі вибираються з загальної кількості N – n не бракованих виробів
способами; при цьому інші m – k виробів повинні бути не бракованими, котрі вибираються з загальної кількості N – n не бракованих виробів  способами. Отже, число сприятливих випадків дорівнює С
способами. Отже, число сприятливих випадків дорівнює С  .
.
Шукана ймовірність дорівнює відношенню числа випадків, сприятливих появі події, до числа всіх елементарних випадків:
Р =  .
.
Наприклад, при N = 100; n = 10; m = 5; k = 3 P = 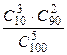
Завдання 2.
Ймовірності влучення в ціль при стрілянині з двох гармат такі: Р1 = 0.8; Р2=0,9. З обох гармат зробили по одному залпу. Знайти ймовірності: а) двох улучень; б) жодного влучення; в) тільки одного влучення; г) хоча б одного влучення.
Розв’язок.
Позначимо події:
А - улучення з першої гармати;
 - невлучення з першої гармати;
- невлучення з першої гармати;
В - улучення з другої гармати;
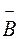 - невлучення з другої гармати.
- невлучення з другої гармати.
Тоді  =
=  ;
; 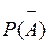 =
= 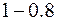 =
= 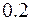 ;
; 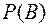 =
=  ;
;  =
=  =
= 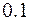 .
.
а) Подія АВ позначає, що мало місце влучення з обох гармат. У свою чергу, події А и В незалежні, отже,
Р(АВ) = Р(А) × Р(В) = 0.8 × 0.9 = 0.72.
б) Подія 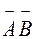 позначає, що мав місце промах (невлучення) з обох
позначає, що мав місце промах (невлучення) з обох
гармат. Тому що події  і
і 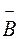 незалежні,
незалежні,
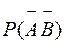 =
= 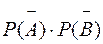 = 0.2 × 0.1 = 0.02.
= 0.2 × 0.1 = 0.02.
в) Подія  +
+ 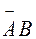 полягає в тому, що мало місце тільки одне влучення: чи влучення з першої гармати, а з другої промах, чи влучення з другої гармати, а з першої промах. Події
полягає в тому, що мало місце тільки одне влучення: чи влучення з першої гармати, а з другої промах, чи влучення з другої гармати, а з першої промах. Події 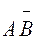 і
і 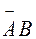 несумісні, тому
несумісні, тому
 +
+  =
= 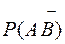 +
+  .
.
Події  і
і 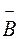 , а також
, а також  і
і  незалежні, отже,
незалежні, отже,
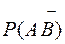 =
= 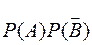 = 0.8 × 0.1 = 0.08;
= 0.8 × 0.1 = 0.08;
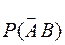 =
= 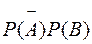 = 0.2 × 0.9 = 0.18;
= 0.2 × 0.9 = 0.18;
 +
+  = 0.08 + 0.18 = 0.26.
= 0.08 + 0.18 = 0.26.
г) Нехай Р – ймовірність того, що має місце хоча б одне влучення. Тоді, враховуючи незалежність подій  і
і 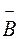 , знайдемо
, знайдемо
Р =  -
-  = 1- 0.2 × 0.1 = 0.98.
= 1- 0.2 × 0.1 = 0.98.
Завдання 3.
Виріб перевіряється на стандартність одним із двох товарознавців. Ймовірність того, що виріб потрапить до першого товарознавця, дорівнює 0.55, а до другого – 0.45. Ймовірність того, що виріб буде визнано стандартним першим товарознавцем, дорівнює 0.9, а другим – 0.98.
Знайти ймовірність того, що: а) виріб, що надійшов на перевірку, буде визнано стандартним; б)виріб перевірив другий товарознавець, якщо воно було визнано стандартним
Розв’язок.
Позначимо події:
А – виріб при перевірці визнано стандартним;
В1 – виріб перевірив перший товарознавець;
В2 – виріб перевірив другий товарознавець.
Події В1 і В2 несумісні і утворюють повну групу.
а) Очевидно, що Р(А/В1) = 0.9 – ймовірність того, що виріб визнаний стандартним першим товарознавцем, а Р(А/В2) = 0.98 – ймовірність того, що виріб визнаний стандартним другим товарознавцем. Згідно з формулою повної ймовірності маємо:
Р(А) = Р(А/В1) × Р(В1) + Р(А/В2)× Р(В2) = 0.9 × 0.55 + 0.98 × 0.495 + 0.441 = 0.936.
б) За умовою задачі необхідно знайти Р(В2/А). Згідно з формулою Бейєса
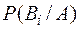 =
=  ,
,
маємо:
Р (В 2 /А) = 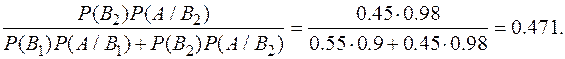
Завдання 4.
Ймовірність того, що навмання узятий виріб нестандартний, дорівнює 0.1. Знайти ймовірність того, що серед узятих п'яти виробів виявиться: а) два нестандартних, б) не більш двох нестандартних.
Розв’язок.
За умовою n = 5; k = 2; p = 0.1; q = 1 – 0.1 = 0.9.
а) Скористаємося формулою Бернуллі


б) Подія А – не більш двох нестандартних виробів, є сума трьох несумісних подій: жодного нестандартного, одне стандартне і два нестандартних.

Завдання 5.
При виготовленні виробів брак складає 5%. Скласти закон розподілу числа бракованих виробів з 6-ти узятих навмання. Знайти М(Х), D(
Розв’язок.
Випадкова величина Х – число бракованих виробів – може приймати значення: 0, 1, 2, 3, 4, 5, 6. Відповідні ймовірності обчислимо за формулою Бернуллі
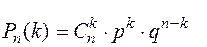
За умовою задачі n = 5; p = 0.05; q = 0.95.
Маємо:
 ;
;
 ;
;
 ;
;
 ;
;
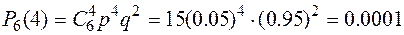 ;
;
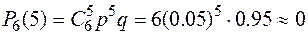 ;
;
 .
.
Отриманий закон розподілу є біномним і має вид
| х | |||||||
| р | 0.7292 | 0.2300 | 0.0386 | 0.0021 | 0.0001 |
Легко перевірити, що 
Математичне сподівання біномного розподілу дорівнює
M(X) = np, а дисперсія дорівнює D(Х) = npq. Отже, маємо:
М(Х) = 6 × 0.05 = 0.3;
D(Х) = 6 × 0.05 × 0.95 = 0.285.
Завдання 6.
Дано інтегральну функцію розподілу випадкової величини Х

Знайти щільність розподілу 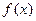 , М(Х), D(Х). Побудувати графіки F(x) і
, М(Х), D(Х). Побудувати графіки F(x) і 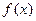 .
.
Розв’язок.
Графік інтегральної функції F(x) 

 |

Диференціальна функція (щільність розподілу):

Її графік
 |
 .
.
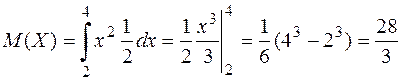 .
.
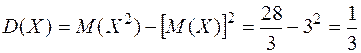 .
.
Завдання 7.
Вага окремого яблука даної партії є випадкова величина Х, розподілена за нормальним законом з математичним сподіванням а = =140 г і середнім квадратичним відхиленням  . Визначити ймовірність того, що вага обраного випадковим образом з даної партії яблука: а) знаходиться від 124 г до 148 г; б) відхиляється від середньої ваги а = 140 г не більш, ніж на
. Визначити ймовірність того, що вага обраного випадковим образом з даної партії яблука: а) знаходиться від 124 г до 148 г; б) відхиляється від середньої ваги а = 140 г не більш, ніж на  8 г.
8 г.
Розв’язок.
Маємо: 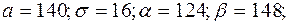
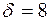
а) Ймовірність того, що вага обраного яблука знаходиться в інтервалі (124; 148) знайдемо по формулі

отже, 
Значення функції Ф(х) знаходимо по таблиці значень функції Лапласа, причому, з огляду на непарність функції Ф(- х) = -Ф(х).
б) Ймовірність того, що вага обраного яблука відхиляється від а не більш, ніж на d, знайдемо за формулою:
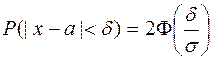 .
.
Маємо: 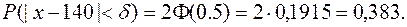
Завдання 8.
При проведенні контрольних іспитів 25 духових шаф були визначені оцінки математичного сподівання і середнього квадратичного відхилення їхнього терміну служби і виявилися рівними  год. і
год. і  год. Вважаючи, що термін служби кожної духової шафи є нормально розподіленою випадковою величиною, визначити надійний інтервал для оцінки невідомого математичного чекання а при довірливій ймовірності (надійності)
год. Вважаючи, що термін служби кожної духової шафи є нормально розподіленою випадковою величиною, визначити надійний інтервал для оцінки невідомого математичного чекання а при довірливій ймовірності (надійності) 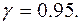
Розв’язок.
Якщо заздалегідь відома величина середнього квадратичного відхилення 
 , то границі надійного інтервалу для оцінки математичного сподівання мають вид
, то границі надійного інтервалу для оцінки математичного сподівання мають вид
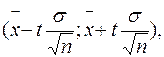
де 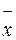 - середнє вибіркове;
- середнє вибіркове;
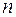 - об’єм вибірки;
- об’єм вибірки;
 - відоме середнє квадратичне відхилення генеральної сукупності;
- відоме середнє квадратичне відхилення генеральної сукупності;
 - величина, що визначається за таблицею значень функції Лапласа
- величина, що визначається за таблицею значень функції Лапласа
 зі співвідношення
зі співвідношення 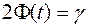 , де
, де  - заздалегідь обрана довірлива ймовірність.
- заздалегідь обрана довірлива ймовірність.
Тому що  , то
, то  По таблиці значень функції Лапласа знаходимо
По таблиці значень функції Лапласа знаходимо 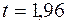 , тоді точність оцінки
, тоді точність оцінки

Нижня границя надійного інтервалу 3000 – 7.84 = 2992.16; а верхня границя 3000 + 7.84 = 3007.84. Таким чином, значення невідомого параметра а, що узгоджуються з даними вибірки, задовольняють нерівності
2992,12 < а < 3007,84.
Варто розуміти, що довірлива ймовірність пов'язана тут не з величиною параметра а, а лише з границями інтервалу, що, очевидно, змінюються при зміні вибірки. Надійність 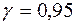 указує на те, що якщо зроблене досить велике число вибірок, то 95% з них визначає такі надійні інтервали, які дійсно містять математичне сподівання і лише в 5% випадків воно може вийти за границі надійного інтервалу.
указує на те, що якщо зроблене досить велике число вибірок, то 95% з них визначає такі надійні інтервали, які дійсно містять математичне сподівання і лише в 5% випадків воно може вийти за границі надійного інтервалу.
Завдання 9.
За даними вибіркового обстеження п’яти крамниць залежність затрат на маркетинг Х (тис. грн.) і обсягом реалізації Y (млн. грн.) має вигляд

 1 3 4 5 7
1 3 4 5 7
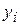 55 85 100 145 115
55 85 100 145 115
Припускаючи, що між Х і Y має місце лінійний кореляційний зв’язок, визначити вибіркове рівняння лінійної регресії.
► Вихідні дані і проміжні розрахунки заносимо в таблицю

| 
| 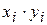
| 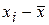
| 
| 
| 
|
| -3 | -45 | |||||
| -1 | -15 | |||||

| 
| 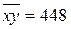
| 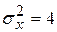
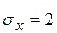
| 

|
Отже, маємо
 .
.
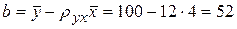 .
.
Отже, шукане рівняння регресії має вигляд
 .
.
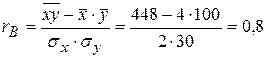 .
.
Розрахунки підтвердили, що між товарообігом і чисельністю робітників обмеженої групи крамниць спостерігається додатний лінійний кореляційний зв’язок, який відповідно таблиці Чеддока можна вважати високим  . ◄
. ◄
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 749; Нарушение авторских прав?; Мы поможем в написании вашей работы!