Дане рівняння приймає вигляд

2 xxtdx +(x ² t ²- x ²)(tdx + xdt)=0.

Скоротивши на х ² , маємо:

2 tdx +(t ²-1) (tdx + xdt)=0;

2 tdx +(t ²-1) tdx + x (t ²-1) dt =0;

t (2+ t ²-1) dx + x (t ²-1) dt =0;

t (1+ t ²) dx = x (1- t ²) dt; .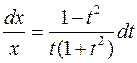

Маємо рівняння з відокремленими змінними відносно х і t. Інтегруючи, знаходимо загальний розв’язок цього рівняння

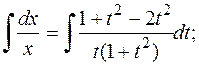
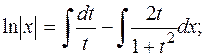
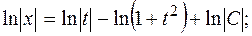
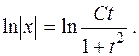
Потенціюючи, знаходимо x = 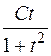, або x (1+ t ²)=C t.

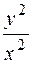Якщо у = хt, то . Отже, x (1+ )= C ,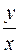

або x ²+ y ²= Cy - загальний інтеграл даного рівняння.

Беручи до уваги початкові дані у (1)=1, маємо:

1+1= С ×1, отже С =2.

Таким чином,

х ²+ у ² =2 у – частинний розв’язок даного рівняння.

б) Дане рівняння є диференційним лінійним рівнянням першого порядку, тому що воно містить шукану функцію у та її похідну у′ в першому степені і має вигляд:

y′+p(x)y=q(x).

Розв’язок шукаємо у вигляді у = UV, де U та V – деякі невідомі функції аргументу х.

Якщо у = UV, то y ′ = U′V+UV ′ і дане рівняння матиме вигляд

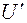V+U 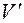-UVtgx = 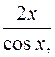, (11.17)

або

V(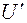 -Utgx)+UV ¢ = .

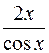Обираємо функцію U таким чином, щоб вираз у дужках дорівнював нулю, тобто

U′-Utgx =0 (11. 18)

тоді

UV ′= 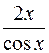. (11.19)

Рівняння (11.18) - є рівняння з відокремлюваними змінними відносно U та х.

Розв’яжемо це рівняння:

; .

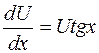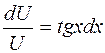Інтегруючи, маємо:

lnU=-ln cosx.

Отже,

U = 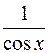- частинний розв’язок рівняння (11.18).

Знайдену функцію U підставляємо в (11.19). Отже,

; V′=2 x;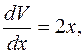

dV = 2 xdx.

Інтегруючи, маємо V = x ²+ C – загальний розв’язок рівняння (11.19).

Таким чином, y = - загальний розв’язок даного рівняння.

Беручи до уваги початкові дані у (0) = 1, маємо 1= ,

отже С =1.

Таким чином, y = - частинний розв’язок даного рівняння. ◄

2. Знайти частинні розв’язки диференціальних рівнянь, що задовольняють початковим умовам:

а) y′′ -3 y ′+2 y =0; y (0)=0; y′ (0)=1.

б) y ''-4 y '+4 y =0; y (0)=0; y '(0)=2.

в) y ''+4 y '+5 y =0; y (0)=2; y '(0)=0.

► а) Дане рівняння є лінійним однорідним рівнянням другого порядку зі сталими коефіцієнтами. Складемо характеристичне рівняння:

K ² - 3 K+ 2 = 0, коренями якого є: K ₁ = 1, K ₂ = 2 - дійсні і різні. Загальний розв’язок цього рівняння має вигляд:

y=C ₁ e^x+C ₂ e ^{2 x} .

Знайдемо частинний розв’язок, що задовольняє початковим умовам. Похідна від загального розв’язку y′=C ₁ e^x+ 2 C ₂ e ^{2 x} .

Підставляючи у загальний розв’язок замість х, у та у ′ відповідні значення за умовою, маємо

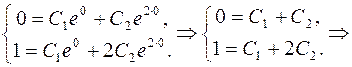
C ₂ = 1, C ₁=1_.

Отже, y= - e^x +e ^{2 x} частинний розв’язок.

б) Дане рівняння є лінійним однорідним рівнянням другого порядку зі сталими коефіцієнтами. Його характеристичне рівняння: K ² - 4 K+ 4 = 0, корені якого K ₁ =K ₂ = 2 – дійсні та рівні. Загальний розв’язок: y=C ₁ e ^{2 x} +C ₂ xe ^{2 x} .

Знайдемо частинний розв’язок, що задовольняє початковим умовам.

y′= 2 C ₁ e ^{2 x} +C ₂ e ^{2 x} + 2 C ₂ xe ^{2 x} .

Враховуючи значення х, у та у ′, маємо:

Отже, y = 2 xe ^{2 x} - частинний розв’язок.

в) Дане рівняння є лінійним однорідним рівнянням другого порядку зі сталими коефіцієнтами. Його характеристичне рівняння:

K ² + 4 K+ 5=0, корені якого є комплексно спряжені числа K ₁ = - 2 + i, K ₂ = - 2 - i

Тому загальний розв’язок має вигляд:

y = e^{- 2 x} (C ₁cos x+C ₂sin x).

Знайдемо частинний розв’язок, враховуючи початкові значення х, у та у ′.

= - 2e^{- 2 x} (C ₁cos x+C ₂sin x) +e^{- 2 x} (- C ₁sin x+C ₂cos x).

Маємо:

.

Отже,

y=e^{- 2 x} (2cos x+ 4sin x) - частинний розв’язок. ◄

3. Знайти частинний розв’язок диференціального рівняння

,

що задовольняє початковим умовам ; .

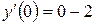► Маємо лінійне неоднорідне диференціальне рівняння другого порядку з постійними коефіцієнтами. Відомо, що загальний розв’язок такого рівняння складається з суми загального розв’язку відповідного однорідного рівняння і частинного розв’язку неоднорідного рівняння, тобто

.

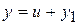Дата добавления: 2014-11-29