Жидкости

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ

Величина давления не зависит от ориентировки, т.е. от угла наклона площадки, к которой приложено давление.

Давление в точке действует нормально к площадке действия и направлено по внутренней нормали.

Другими словами, т.к. жидкость практически не способна сопротивляться растяжению, а в покоящейся жидкости не действуют касательные силы, то на неподвижную жидкость могут действовать только силы давления.

Причем на внешней поверхности рассматриваемого объема жидкости силы давления всегда направлены по нормали во внутрь объема и, следовательно, являются сжимающими.

Этот вывод является выражением известного закона Паскаля, гласящего, что:

«Давление на поверхность жидкости, произведенное внешними силами, передается жидкостью одинаково во всех направлениях».

Очевидно, что если давление P не зависит от ориентации площадки, проходящей через данную точку и определяется только положением точки в жидкости, то давление P есть функция только координат, т.е.

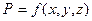
Дифференциальные уравнения равновесия жидкости получаются на основе векторной суммы объемных и поверхностных сил, действующих на мысленно выделенный элементарный объем жидкости.

c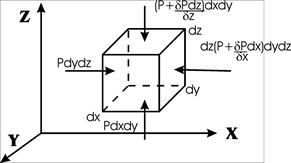

Рис. 3 Равновесие элементарного прямоугольного параллелепипеда

1. Рассмотрим равновесие элементарного прямоугольного параллелепипеда со сторонами dx, dy, dz, выделенного внутри покоящейся жидкости.
2. Пусть на единицу массы параллелепипеда действует массовая сила F, с ее составляющими X,Y,Z
3. Если на три грани, пересекающиеся в(.) 0 будет действовать давление P, то на соответствующих противоположных гранях давления будут равны:

; ;

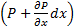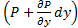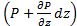
4. Уравнение равновесия в проекции на ось X будет иметь вид:

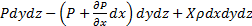=0

раскрыв скобки получим:

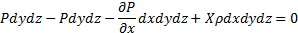
отнеся к единице объема получим:

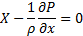
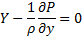
Эти уравнения были получены Эйлером в 1755 году и называются ур. Эйлера равновесия жидкости и газа. Они являются основными уравнениями гидростатики.

1. Если эту систему уравнений умножим последовательно на dx, dy, dz и сложим, то получим:

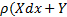dy+Zd )=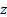

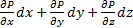
т.к. P = f(x,y,z), то правая часть последнего уравнения есть полный дифференциал

dP=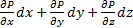

тогда имеем:

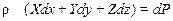
Так как имеет место равновесие жидкости и правая часть уравнения является полным дифференциалом некоторой функции, зависящей от координат, то полным дифференциалом некоторой функции, зависящей от координат должна быть и левая часть уравнения.

Обозначим эту функцию через Ф

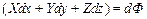
Т.к. она есть функция только координат и т.к. частные производные ее по координатам дают соответствующие проекции (X,Y,Z) объемной силы, отнесенной к единице массы жидкости, то следовательно функция Ф. является потенциальной функцией. Объемная же сила F, удовлетворяющая условиям является силой, имеющей потенциал.

С другой стороны полный дифференциал можно представить как сумму частных дифференциалов

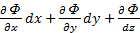dz=dФ

Сопоставляя два последние уравнения видим, что

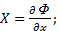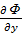Y= ; Z=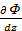

Тогда уравнение представляется таким образом:

ρdФ = dP

Из этого уравнения следует, что «жидкость может находиться в равновесии только в том случае, когда массовые силы, действующие в ней, имеют потенциал, т.е. проекции массовых сил удовлетворяют условию».

Дата добавления: 2014-12-07