Скорость химических реакций 3 страница

Энергия Гиббса window.top.document.title = "4.6. Энергия Гиббса";

Самопроизвольное протекание изобарно-изотермического процесса определяется двумя факторами: энтальпийным, связанным с уменьшением энтальпии системы (ΔH), и энтропийным TΔS, обусловленным увеличением беспорядка в системе вследствие роста ее энтропии. Разность этих термодинамических факторов является функцией состояния системы, называемой изобарно-изотермическим потенциалом или свободной энергией Гиббса (G, кДж):

ΔG = ΔH – TΔS

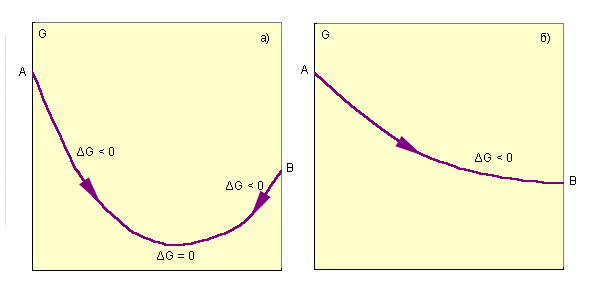
При ΔG < 0 реакция термодинамически разрешена и система стремится к достижению условия ΔG = 0, при котором наступает равновесное состояние обратимого процесса; ΔG > 0 указывает на то, что процесс термодинамически запрещен.

Изменение энергии Гиббса: а – обратимый процесс; б – необратимый процесс.

Записав уравнение в виде ΔH = ΔG + TΔS, получим, что энтальпия реакции включает свободную энергию Гиббса и «несвободную» энергию ΔS∙T. Энергия Гиббса, представляющая собой убыль изобарного (P = const) потенциала, равна максимальной полезной работе. Уменьшаясь с течением химического процесса, ΔG достигает минимума в момент равновесия (ΔG = 0). Второе слагаемое ΔS∙T (энтропийный фактор) представляет ту часть энергии системы, которая при данной температуре не может быть превращена в работу. Эта связанная энергия способна лишь рассеиваться в окружающую среду в виде тепла (рост хаотичности системы).

Итак, в химических процессах одновременно изменяются энергетический запас системы (энтальпийный фактор) и степень ее беспорядка (энтропийный фактор, не совершающая работу энергия).

Анализ уравнения ΔG = ΔH - TΔS, позволяет установить, какой из факторов, составляющих энергию Гиббса, ответственен за направление протекания химической реакции, энтальпийный (ΔH) или энтропийный (ΔS∙T).

· Если ΔH < 0 и ΔS > 0, то всегда ΔG < 0 и реакция возможна при любой температуре.

· Если ΔH > 0 и ΔS < 0, то всегда ΔG > 0, и реакция с поглощением теплоты и уменьшением энтропии невозможна ни при каких условиях.

· В остальных случаях (ΔH < 0, ΔS < 0 и ΔH > 0, ΔS > 0) знак ΔG зависит от соотношения ΔH и TΔS. Реакция возможна, если она сопровождается уменьшением изобарного потенциала; при комнатной температуре, когда значение T невелико, значение TΔS также невелико, и обычно изменение энтальпии больше TΔS. Поэтому большинство реакций, протекающих при комнатной температуре, экзотермичны. Чем выше температура, тем больше TΔS, и даже эндотермические реакции становятся осуществляемыми.

Проиллюстрируем эти четыре случая соответствующими реакциями:

1.	ΔH < 0 ΔS > 0 ΔG < 0	C2H5–O–C2H5 + 6O2 = 4CO2 + 5H2O (реакция возможна при любой температуре)
2.	ΔH > 0 ΔS < 0 ΔG > 0	реакция невозможна
3.	ΔH < 0 ΔS < 0 ΔG > 0, ΔG < 0	N2 + 3H2 = 2NH3 (возможна при низкой температуре)
4.	ΔH > 0 ΔS > 0 ΔG > 0, ΔG < 0	N2O4(г) = 2NO2(г) (возможна при высокой температуре).

Для оценки знака ΔG реакции важно знать величины ΔH и ΔS наиболее типичных процессов. ΔH образования сложных веществ и ΔH реакции лежат в пределах 80–800 кДж∙моль^–1. Энтальпия реакции сгорания ΔН⁰_сгор всегда отрицательна и составляет тысячи кДж∙моль^–1. Энтальпии фазовых переходов обычно меньше энтальпий образования и химической реакции ΔH_пар – десятки кДж∙моль^–1, ΔH_крист и ΔН_плавл равны 5–25 кДж∙моль^–1.

Зависимость ΔН от температуры выражается соотношением ΔН_т = ΔН⁰ + ΔС_p∙ΔT, где ΔС_p – изменение теплоемкости системы. Если в интервале температур 298 К – Т реагенты не претерпевают фазовых превращений, то ΔС_p = 0, и для расчетов можно пользоваться значениями ΔН⁰.

Энтропия индивидуальных веществ всегда больше нуля и составляет от десятков до сотен Дж∙моль^–1K^–1 (табл.). Знак ΔG определяет направление реального процесса. Однако для оценки осуществимости процесса обычно пользуются значениями стандартной энергии Гиббса ΔG⁰. Величина ΔG⁰ не может использоваться в качестве критерия вероятности в эндотермических процессах со значительным возрастанием энтропии (фазовые переходы, реакции термического разложнения с образованием газообразных веществ и др.). Такие процессы могут быть осуществлены за счет энтропийного фактора при условии Тñ ΔН⁰ _¤ ΔS⁰

Химическое равновесие window.top.document.title = "4.7. Химическое равновесие";

Для определения величины ΔG в условиях, отличных от стандартных, используют уравнение зависимости изобарно-изотермического потенциала от концентрации и температуры получаем:

ΔG = ΔU + PΔV – TΔS

Рассмотрим вместо небольших, но конечных изменений (ΔG, ΔH, ΔS) бесконечно малые изменения всех параметров, входящих в уравнение. Тогда уравнение приобретает вид:

dG = dU + PdV + VdP – TdS – SdT.

Подставив в него dU = δQ – δA, получим: dG = δQ – δA + PdV + VdP – TdS – SdT.

Если реакция протекает при постоянной температуре (SdT = 0) и обратимо (ΔQ = TdS), а единственной совершаемой в ходе реакции работой является работа расширения (δА = PdV), то в правой части все члены, кроме VdP, взаимно сокращаются или равны нулю. Тогда получаем: dG = VdP.

Для одного моля идеального газа V = RT / P и, следовательно, dG = RT dP / P = RT d(lnP)

Интегрируя, получаем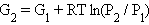

Это уравнение позволяет, зная молярную энергию Гиббса идеального газа G₁ при парциальном давлении P₁, вычислить молярную энергию Гиббса G₂ при парциальном давлении Р₂. Хотя уравнение 4.6 выведено для обратимой реакции, оно в равной мере применимо и к необратимым процессам, поскольку G является функцией состояния, и ее изменение не зависят от способа перехода из состояния 1 в состояние 2. Допустив, что состояние 1 является стандартным, а состояние 2 произвольным, уравнение можно записать в виде: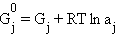

где 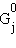– стандартный изобарно-изотермический потенциал вещества j; a_j – P/P⁰ – его активная концентрация (активность).

Для идеальных растворов активная концентрация определяется как отношение концентрации этого вещества при заданных условиях к его концентрации в стандартном состоянии а = С/C⁰. Вещества в стандартном состоянии имеют а = 1.

В соответствии с тем,что энергия Гиббса произвольной химической реакции

aA + вВ = lL + mM

равна: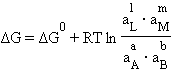

При достижении равновесия (ΔG = 0) уравнение принимает вид

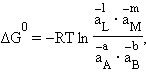
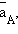
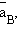
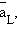
где 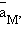– равновесные значения активных концентраций.

Выражение под знаком логарифма, представляющее собой отношение произведения равновесных активностей продуктов к произведению активностей исходных веществ в степенях их стехиометрических коэффициентов, называется константой равновесия:

Исходя из них, получим уравнение, носящее название изотермы Вант-Гоффа:

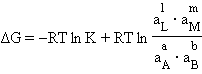
При определенных условиях активности реагентов могут быть заменены концентрациями или парциальными давлениями. В этих случаях константа равновесия, выраженная через равновесные концентрации K_c или через парциальные давления K_р, принимает вид

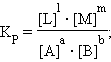
Уравнения представляют собой варианты закона действующих масс (ЗДМ) для обратимых реакций в состоянии равновесия. При постоянной температуре отношение равновесных концентраций (парциальных давлений) конечных продуктов к равновесным концентрациям (парциальным давлениям) исходных реагентов, возведенных соответственно в степени, равные их стехиометрическим коэффициентам, величина постоянная (К. Гульберг, П. Вааге, 1867 г.).

Для газообразных веществ K_p и K_c связаны соотношением K_p = (RT)^ΔnK_c, где Δn – разность числа молей начальных и конечных газообразных реагентов.

Константа равновесия определяется при известных равновесных концентрациях реагирующих веществ или по известной ΔG⁰ химической реакции.

Принцип Ле Шателье window.top.document.title = "4.8. Принцип Ле Шателье";

При известных ΔH реакции или при Δn ≠ 0 на химическое равновесие можно воздействовать изменением температуры или давления. Химическое равновесие может быть смещено изменением концентраций реагентов. Другими словами, равновесие можно сместить внешним воздействием, руководствуясь принципом Ле Шателье: если на равновесную систему оказывать внешнее воздействие, то равновесие смещается в сторону, противодействующую этому воздействию.

1. Влияние температуры. Для реакций, идущих с уменьшением энтальпии (экзотермических), повышение температуры будет препятствовать протеканию прямого процесса, то есть смещать реакцию в сторону исходных веществ. Эндотермические реакции при этом будут смещаться в сторону конечных продуктов. Например, при обычных условиях реакция N₂ + O₂ не идет (ΔН > 0), но повышение температуры может сделать эти реакцию осуществимой. Реакция CO + 1/2O₂ = CO₂, ΔH < 0 с повышением температуры будут смещаться в сторону исходных веществ.

2. Влияние давления. Если реагируют газообразные вещества, то при неизменном числе молей начальных и конечных реагентов повышение общего давления не приведет к смещению равновесия. Если число молей при реакции меняется, то изменение общего давления приведет к смещению равновесия. В частности, реакция 2CO + O₂ = 2CO₂, протекающая с уменьшением Δn, при повышении общего давления сместится в сторону образования СO₂.

3. Влияние концентраций. В тех реакциях, в которых лучше оперировать концентрациями (реакции в растворах), увеличение концентраций исходных веществ приводит к смещению равновесия в сторону конечных продуктов и наоборот. Так, в реакции этерификации (образование сложного эфира)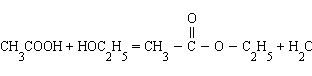

4. увеличение концентрации уксусной кислоты или этанола увеличивает выход этилацетата, а добавление в систему воды приводит к омылению, т. е. образованию исходных продуктов.

КИНЕТИКА ХИМИЧЕСКИХ РЕАКЦИЙ

Скорость химических реакций

Химическое равновесие

Скорость реакции определяется изменением молярной концентрации одного из реагирующих веществ:

V = ±С₂ – С₁t₂ - t₁= ±DС / Dt)

где С₁ и С₂ - молярные концентрации веществ в моменты времени t₁ и t₂ соответственно (знак (+) – если скорость определяется по продукту реакции, знак (–) – по исходному веществу).

Реакции происходят при столкновении молекул реагирующих веществ. Ее скорость определяется количеством столкновений и вероятностью того, что они приведут к превращению. Число столкновений определяется концентрациями реагирующих веществ, а вероятность реакции - энергией сталкивающихся молекул.

Дата добавления: 2014-12-07