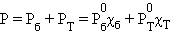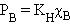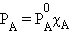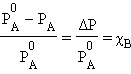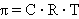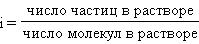Растворы неэлектролитов. window.top.document.title = "6.3

window.top.document.title = "6.3. Растворы неэлектролитов";

По термодинамическому признаку растворы делятся на идеальные и реальные. Для идеальных растворов предполагается, что между компонентами раствора любыми взаимодействиями можно пренебречь. Следовательно, любое свойство растворяемых веществ при их смешении не должно меняться. Например, при смешении близких по свойствам бензола и толуола давление пара P над раствором в соответствии с законом Дальтона будет аддитивной величиной

Здесь 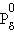и χ_δ, и χ_T – соответственно давление и мольные доли бензола и толуола.

Зависимость давления пара над смесью бензол–толуол от мольной доли.

Если раствор сохраняет свойства идеальности при любых концентрациях, его называют совершенным (растворы изотопов). Часто раствор приобретает эти качества только при достаточно большом разведении, это – «бесконечно разбавленный» раствор при χ→0. Во всех прочих случаях раствор считается реальным.

Взаимодействие между компонентами раствора, выражаемое через энтальпию сольвации ΔH_сольв, служит в определенных пределах мерой идеальности раствора. Д. И. Менделеев показал, что взаимодействие между компонентами раствора может рассматриваться как химический процесс образования соединений переменного состава – сольватов. Этот подход лежит в основе химической или сольватной теории растворов. Если при кристаллизации твердая фаза содержит молекулы растворителя, то ее называют кристаллосольватом.

Закон Генри window.top.document.title = "6.3.1. Закон Генри";

Если растворенное вещество характеризуется большой упругостью пара по сравнению с упругостью пара растворителя (P_B >> P_A) и при этом оба компонента раствора химически инертны, то растворение такого газообразного вещества в жидкости подчиняется закону Генри: при постоянной температуре давление летучего (газообразного) компонента P_B прямо пропорционально его мольной доле χ_B:

K_H – константа Генри.

В табл. приведены константы Генри некоторых газов для воды.

Газ	H2	He	Ar	N2	O2	CO2
KГ						29,3

Константы Генри для воды при 298 K.

Из уравнения следует, что K_H определяется выбором единиц давления и концентрации

Законы Рауля window.top.document.title = "6.3.2. Законы Рауля";

Если упругость пара растворенного вещества очень мала P_B << P_A, то его парциальным давлением можно пренебречь (нелетучий компонент), и тогда упругость пара над раствором будет зависеть только от парциального давления растворителя:

Это первый закон Рауля – парциальное давление над раствором прямо пропорционально мольной доле растворенного вещества. После подстановки χ_A = 1 – χ_B и несложных преобразований

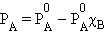
получаем

Относительное понижение упругости пара над раствором равно мольной доле растворенного вещества. Это закон Рауля для нелетучего растворенного компонента. Из этого закона можно вывести два следствия, которые в объединенном виде формируются как второй закон Рауля.

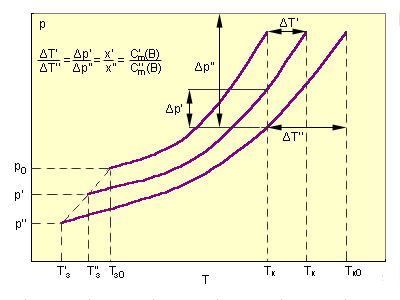
Зависимость повышения температуры кипения ΔT_кип и понижения температуры замерзания ΔT_зам раствора от концентрации растворенного вещества.

На рис. приведены зависимости P(T) чистого растворителя и двух его растворов P'(T) и P''(T).

Выразим мольную долю χⁱ через моляльную концентрацию 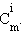Для двухкомпонентного раствора χ_B = 1 – χ_A. При C_m << 1 получим

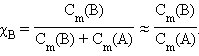
Из подобия треугольников следует

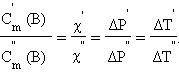
По определению, при 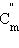(B) = 1 моль∙кг^–1 повышение температуры 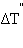равно K_эб – эбулиоскопической константе для данного растворителя. Тогда повышение температуры кипения для данного раствора будет пропорционально его моляльной концентрации:

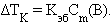
Проведя аналогичное исследование, касающееся понижения температуры замерзания раствора, получим

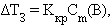
где K_кр – криоскопическая константа.

Второй закон Рауля – понижение температуры кипения и повышение температуры замерзания раствора прямо пропорционально моляльной концентрации раствора:

K_эб и K_кр являются экстраполяционными величинами от малых концентраций растворенного вещества, где выполняется этот закон, на C_m(B) = 1, где этот закон уже не действует. В табл. приведены K_кр и K_эф для воды и бензола.

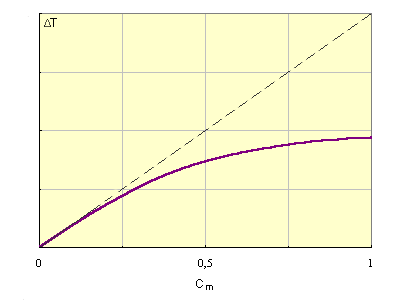
Иллюстрация справедливости второго закона Рауля для разбавленных растворов и экстраполяционной природы K_кр и K_эб.

	Kкр	Kэб
вода	1,86	0,52
бензол	5,07	2,60

Криоскопические и эбулиоскопические константы для воды и бензола (град∙моль^–1∙кг).

Второй закон Рауля дает легко осуществимую экспериментально возможность определения молекулярных масс некоторых молекулярных соединений, неспособных к диссоциации в данном растворителе. Действительно, моляльная концентрация растворенного вещества может быть представлена в виде соотношения C_m = g_B ∙ 1000 / μ_B ∙ g_A, где g_A – вес растворителя, g_B – вес растворенного вещества, μ_B – его молярная масса. Тогда из ΔT = K_кр ∙ m получим молярную массу растворенного вещества:

Осмос window.top.document.title = "6.3.3. Осмос";

Если система, разделенная мембраной, представляет собой растворы, в которых через мембрану способны проходить только молекулы растворителя, то свойства ее будут определяться разностью мольных долей (концентраций) растворителя по обе стороны мембраны.

Явление, связанное со способностью проходить через мембрану, в частности, только молекул растворителя, называется осмосом, а вызываемое им изменение давления по обе стороны мембраны – осмотическим давлением. Явление осмоса чрезвычайно разнообразно и во многом определяется природой мембраны и компонентов раствора.

Представим, что сосуд с двумя горлами для залива раствора разделен мембраной M (рис.). В каждую часть сосуда зальем растворы, отличающиеся только концентрацией. Поскольку мольные доли растворителя по обе стороны мембраны не совпадают, то стремление их к выравниванию приведет к переходу части растворителя в ту часть сосуда, где концентрация растворенного вещества больше. Увеличение количества растворителя эквивалентно возрастанию давления, и если мембрана способна к деформации, она изогнется в сторону с меньшей концентрацией растворенного вещества (рис. а).

Если мембрана жесткая, то в отсеке с большей концентрацией количество растворителя будет возрастать до тех пор, пока гидростатическое давление h (рис. б) не станет равным осмотическому давлению и не прекратит осмос.

Схема разности осмотических давлений при χ₁ < χ₂ при эластичной (а) и жесткой (б) мембранах.

Осмотическое давление π – внутреннее давление растворенного вещества, численно равное тому внешнему давлению, которое нужно приложить, чтобы прекратить осмос; оно зависит от температуры и концентрации.

Эту зависимость Вант-Гофф уподобил поведению идеального газа:

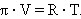
По Вант-Гоффу осмотическое давление раствора численно равно тому газовому давлению, которое имело бы растворенное вещество, будучи переведенным в газообразное состояние в том же объеме и при той же температуре. Поскольку объем (разбавление) обратно пропорционален концентрации, то закон Вант-Гоффа можно записать в виде

Так как объем одного моля газообразного вещества при нормальных условиях равен 22,4 литра, то осмотическое давление раствора, содержащего 1 моль вещества, равно 22,4 атм.

Измерение осмотического давления раствора используется для определения молекулярных масс даже разбавленных растворов, что позволяет оценивать молекулярные массы растворимых высокомолекулярных соединений, в частности, биополимеров. Заменив C(B) в формуле Вант-Гоффа соотношением (m(B) ∙ 1000 / μ(B) ∙ V), получим уравнение, позволяющее вычислять молекулярные массы растворенных веществ:

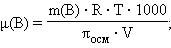
m(B) – масса растворенного вещества, V – объем раствора.

Если растворы характеризуются одинаковыми осмотическими давлениями, то по Вант-Гоффу такие растворы называются изотоническими. Независимо от природы растворенного вещества, изотоничность является следствием одинакового числа частиц в растворе.

Поскольку при растворении реальное число частиц может отличаться от числа растворенных молекул, Вант-Гофф ввел понятие изотонического коэффициента i. По определению это отношение числа всех частиц к числу растворенных молекул:

В бензольном растворе уксусной кислоты i < 1, ибо в этом растворе число частиц меньше числа молекул, в результате реакции ассоциации в соответствие с уравнением

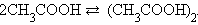
Если же в растворе преобладает не ассоциативный, а диссоциативный или ионизационный механизмы взаимодействия, то i > 1. Так, в водном растворе уксусная кислота диссоциирует CH₃COOH = CH₃COO^– + H⁺, и число частиц становится больше числа молекул.

ЭЛЕКТРОЛИТИЧЕСКАЯ ДИССОЦИАЦИЯ
ЭЛЕКТРОЛИТЫ И НЕЭЛЕКТРОЛИТЫ

Дата добавления: 2014-12-07