Можно ли не решать неравенства

Что делать в частных случаях.

Частные случаи тригонометрических уравнений – это когда справа стоит 0 или 1 или -1

Если в неравенстве справа 0 (например, sinx>0), то неравенство решается как обычно, то есть обводится дуга окружности между двумя точками – это как раз получится половина окружности.

Если же в неравенстве справа 1 или -1 (например, cosx<1), то точка на окружности только одна. Здесь надо вспомнить, что синус и косинус находятся в диапазоне от -1 до +1, поэтому неравенства sinx>1 (cosx>1, cinx<-1, cosx<-1) не имеют решений. Ну а если неравенства нестрогие (например, sinx>=1), то решением является эта самая единственная точка. Для неравенств типа sinx<=1 (cosx<=1, sinx>=-1, cosx>=-1) решением будет любое число (вся окружность), а если неравенство строгое (например, sinx<1) – то вся окружность кроме этой единственной точки.

Рисунки можно нарисовать самостоятельно. J

Обычно в задачах ЕГЭ решение тригонометрического неравенства требуется для того, чтобы найти область определения при решении уравнений. Но ведь если мы решаем уравнение, мы получим конкретные корни. А значит, можно не находить в явном виде область определения, а только записать задающее ее неравенство, а потом проверить, удовлетворяют ли получившиеся корни этому неравеству.

Пример:

Решить уравнение: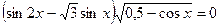

Записываем ОДЗ: 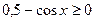, но не решаем получившееся неравенство, а находим корни уравнения:

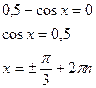
А теперь проверяем каждый корень на соответствие ОДЗ:

Первый корень πn. Здесь возможны два варианта: если х=2 πn, то cosx=1, и 0,5-cosx<0 – не удовлетворяет ОДЗ. Если же x=π+2πn, то cosx=-1, 0,5-cosx>0 – удовлетворяет ОДЗ.

Второй корень ± π/6+2 πn. В этом случае cosx=√3/2, но √3/2>0,5, значит, 0,5-cosx<0 – не удовлетворяет ОДЗ.

Третий корень ± π/3+2 πn, естественно, удовлетворяет ОДЗ – под корнем будет 0.

Получается, что от всех корней нам остались только 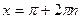и 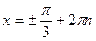. Это и будет ответ

Дата добавления: 2014-12-08