
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила вычисления пределов
|
|
|
|
Основные учебные элементы модуля
Основные понятия модуля
Алгоритм самостоятельной работы
Модуль 4. Введение в математический анализ
При изучении модуля «Введение в математический анализ» студент должен самостоятельно выполнить следующие действия:
- ознакомиться с языком дисциплины
- ознакомиться с основными вопросами и учебными элементами модуля
- ознакомиться с перечнем умений по данному модулю
- выполнить предложенный вариант домашнего задания
- выполнить тест-тренинг
| Понятие модуля | Обозначение, формула |
| Функция | см. опорную схему |
| Последовательность | см. опорную схему |
| Предел | см. опорную схему |
| Непрерывность | см. опорную схему |
| Учебные элементы | Название | Обозначение, формула |
| Уч. элемент № 1 | Основные понятия и способы задания функций | см. опорную схему |
| Уч. элемент № 2 | Последовательность и ее предел | см. опорную схему |
| Уч. элемент № 3 | Предел функции | см. опорную схему |
| Уч. элемент № 4 | Бесконечно большие и бесконечно малые функции, их взаимосвязь | см. опорную схему |
| Уч. элемент № 5 | Основные теоремы о пределах | см. опорную схему |
| Уч. элемент № 6 | Первый замечательный предел | см. опорную схему |
| Уч. элемент № 7 | Второй замечательный предел | см. опорную схему |
| Уч. элемент № 8 | Понятие непрерывности | см. опорную схему |
| Уч. элемент № 9 | Точки разрыва | см. опорную схему |
| Уч. элемент № 10 | Свойства непрерывных функций | см. опорную схему |
Опорная схема
1. Раскрытие неопределенности вида  .
.
а. 
Для того чтобы определить предел дробно-рациональной функции, когда числитель и знаменатель дроби при 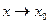 имеют пределы равные нулю, надо числитель и знаменатель дроби разделить на
имеют пределы равные нулю, надо числитель и знаменатель дроби разделить на 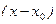 и перейти к пределу. Если после этого числитель и знаменатель новой дроби имеют пределы равные нулю при
и перейти к пределу. Если после этого числитель и знаменатель новой дроби имеют пределы равные нулю при 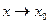 , то надо произвести повторное деление на
, то надо произвести повторное деление на 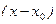 .
.
б. 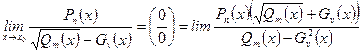
Чтобы найти предел дроби, содержащей иррациональные выражения в случае, когда пределы числителя и знаменателя дроби равны нулю, надо перенести иррациональность из числителя в знаменатель или из знаменателя в числитель и после этого сделать необходимые упрощения (приведение подобных членов, сокращения и т.п.) и перейти к пределу.
2. Раскрытие неопределенности вида  .
.
Предел отношения двух многочленов одинаковых степеней равен отношению коэффициентов при старших степенях, Если степень числителя меньше знаменателя, то предел равен нулю, а если степень числителя больше знаменателя, то предел равен бесконечности.
3. Раскрытие неопределенности вида  .
.
Привести функцию стоящую под знаком предела к неопределенности вида  . И раскрыть ее по рассмотренному выше правилу.
. И раскрыть ее по рассмотренному выше правилу.
2. Первый замечательный предел 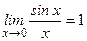
Важнейшие эквивалентности
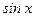 ~ х, при ~ х, при 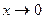
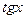 ~ х, при ~ х, при 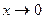
 ~ х, при ~ х, при 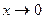
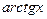 ~ х, при ~ х, при 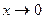
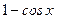 ~ ~ 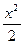 , при , при 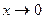
| 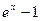 ~ х, при ~ х, при 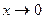
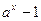 ~ ~ 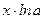 , при , при 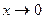
 ~ х, при ~ х, при 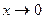
 ~ ~ 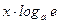 , при , при 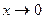
|
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 966; Нарушение авторских прав?; Мы поможем в написании вашей работы!