Простейшие случаи криволинейной корреляции

Определение: Если график регрессии 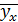= ƒ(x) или 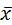_у = φ(y) изображается кривой линией, то корреляцию называют криволинейной.

Например, функции регрессии Y на X могут иметь вид:

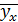= ax² + bx + c – параболическая корреляция второго порядка;

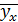= ax ³ + bx² + cx + d – параболическая корреляция третьего порядка.

Для того чтобы определить вид функции регрессии строят точки (x, 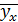) и по их расположению делают заключение о примерном виде функции регрессии. При окончательном решении принимают во внимание особенности, вытекающие из сущности решаемой задачи.

Теория криволинейной корреляции решает те задачи, что и теория линейной корреляции (установление формы и тесноты корреляционной связи).

Рассмотрим параболическую корреляцию второго порядка. Предположим, что данные n наблюдений (выборка) позволяют считать, что имеет место именно такая корреляция. В этом случае выборочное уравнение регрессии Y на X имеет вид:

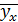=Ax² + Bx + C (1),

где A, B, C – неизвестные параметры.

Пользуясь методом наименьших квадратов, получаем систему линейных уравнений относительно неизвестных параметров (предлагаем вывести ее самостоятельно):

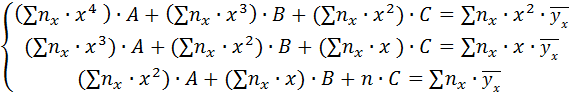
(2)

Найденные из системы (2) параметры A, B, C подставляем в формулу (1), в итоге получаем искомое уравнение регрессии.

Пример: Найти выборочное уравнение регрессии Y на X вида 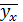= Ax² + Bx + C по данным корреляционной таблицы.

Y \ X		1,1	1,2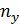
			-
	-		-
7,5	-
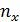
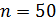
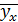
		6,95	7,5

Решение: Составим расчетную таблицу.

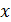
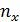
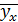
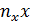
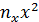
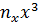
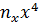
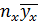
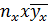
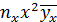
1,1		6,95	36,3	39,93	43,93	48,32	229,35	252,3	277,5
1,2		7,5	10,8	12,96	15,55	18,66	67,5		97,2
		-	55,1	60,89	67,48	74,98	344,85	381,3	422,7

Подставив числа (суммы) нижней строки таблицы в систему (2), получим:

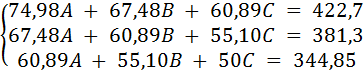
Решив эту систему, получаем: A = 1,94; В = 2,98; С = 1,1. Тогда искомое уравнение принимает вид:

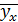= 1,94x² + 2,98x + 1,1.

Например, при x₁=1 найдем по таблице
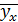= 6, а по уравнению 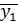=1,94 + 2,98 + 1,1 = 6,02.

Таким образом, найденное уравнение хорошо согласуется с данными выборки.

Дата добавления: 2014-12-27