Выборочное корреляционное отношение

Поставим вопрос: Как оценить тесноту любой корреляционной связи?

Пусть данные наблюдений над количественными признаками X и Y сведены в корреляционную таблицу. Можно считать, что тем самым наблюдаемые значения Y разбиты на группы. Каждая группа содержит те значения Y, которые соответствуют определенному значению X.

Пример: Данакорреляционная таблица

Y \ X
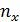
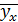
	4,2	3,7

Здесь 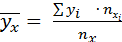, таким образом:

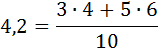
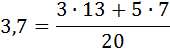
К первой группе относятся те 10 значений Y (4 раза встречается значение 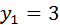и 6 раз – значение 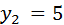), которые соответствуют значению .

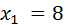Ко второй группе относятся те 20 значений Y, которые соответствуют значению .

Условные средние теперь можно назвать групповыми средними: групповая средняя первой группы 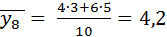; групповая средняя второй группы 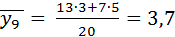. Так как все значения признака Y разбиты на группы, можно представить общую дисперсию признака в виде:

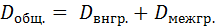(1)

Докажем справедливость следующих утверждений:

1) Если признак Y связан с признаком X функциональной зависимостью, то .

2) Если признак Y связан с признаком X корреляционной зависимостью, то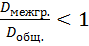

Доказательство:

1) Если признак Y связан с признаком X функциональной зависимостью, то определенному значению X соответствует одно значение Y. В этом случае в каждой группе содержатся равные между собой значения Y. Следовательно, 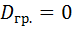для каждой группы.

Например, если значению 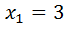соответствует значение 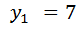и 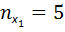, то в группе содержится 5 значений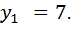

Следовательно, средняя арифметическая групповых дисперсий (взвешенная по объемам групп), т.е. внутригрупповая дисперсия и формула (1) имеет вид: . Что и требовалось доказать.

2) Если признак Y связан с признаком X корреляционной зависимостью, то определенному значению X соответствуют различные значения Y (образующие группу).

В этом случае 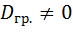для каждой группы. Следовательно, средняя арифметическая групповых дисперсий, (взвешенная по объемам групп) 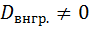. Тогда одно положительное слагаемое меньше суммы двух положительных слагаемых

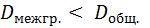=> < 1.

Что и требовалось доказать.

Уже из приведённых рассуждений видно, что чем связь между признаками X и Y ближе к функциональной, тем меньше и, следовательно, тем больше 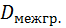приближается к

Тогда дробь стремится к единице:

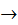1.

Целесообразно, в качестве меры тесноты корреляционной зависимости рассматривать 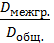или .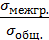

Для оценки тесноты линейной корреляционной связи между признаками X и Y в выборке служит выборочный коэффициент корреляции. В случае нелинейной корреляции выборочный коэффициент корреляции утрачивает своё значение, как мера связи.

Для оценки тесноты нелинейной корреляционной связи вводятся новые сводные характеристики:

– выборочное корреляционное отношение Y к X (греческая буква «эта»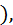

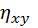– выборочное корреляционное отношение X к Y.

Определение: Выборочным корреляционным отношением признака Y к признаку X называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению признака Y:

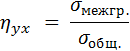
или в других обозначениях

,

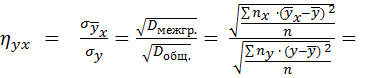
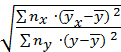где n – объем выборки;

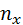– частота значения x признака X;

частота значения y признака Y;

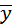– общая средняя признака Y;

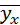– условная средняя признака Y.

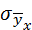– межгрупповое среднее квадратическое отклонение.

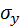– общее среднее квадратическое отклонение.

Аналогично определяется выборочное корреляционное отношение признака X к признаку Y:

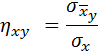
Пример: По данным корреляционной таблицы найти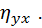

Y \ X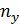
		-

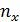
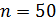
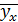
Решение:

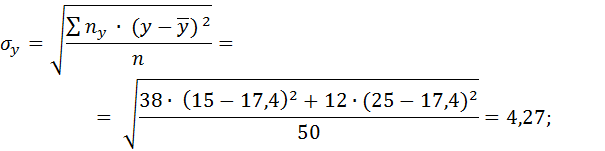
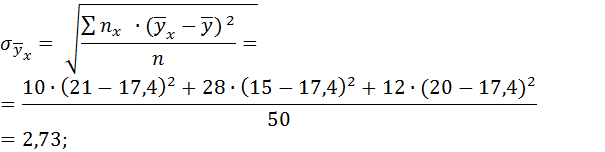
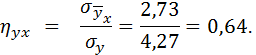
Дата добавления: 2014-12-27