Основные формулы комбинаторики

Комбинаторика изучает количества комбинаций, подчинённых определённым условиям, которые можно составить из элементов любой природы, заданного конечного множества.

Приведем определения основных комбинаций и формулы для вычисления.

Определение: Перестановками называются комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения.

Число P_n всех возможных перестановок вычисляют по формуле:

P_n = n!

где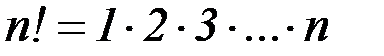

Заметим, что, по определению, 0! = 1, а 1! = 1.

Пример: Сколько трёхзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?

Решение: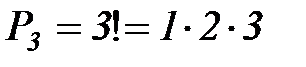

Определение: Размещениями называются комбинации, составленные из n различных элементов по m элементов (m ≤ n), которые отличаются либо составом элементов, либо их порядком.

Число 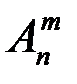всех возможных размещений вычисляют по формуле:

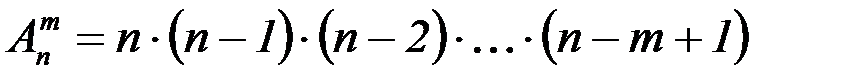
Пример: Сколькими способами можно рассадить четырех студентов на десяти свободных местах?

Решение: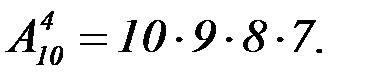

Пример: Сколько трёхзначных чисел можно составить из семи различных цифр при отсутствии среди них нуля?

Решение: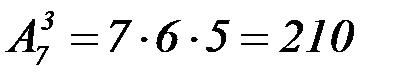

Определение: Сочетаниями называются комбинации, составление из n различных элементов по m элементов (m ≤ n), которые отличаются хотя бы одним элементом.

Число сочетаний 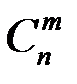вычисляют по формуле:

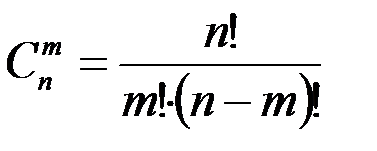
Пример: Сколькими способами можно выбрать две детали из ящика, содержащего десять деталей?

Решение: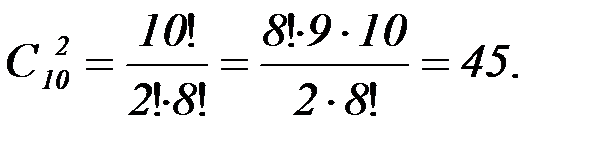

Для числа сочетаний справедливы равенства:

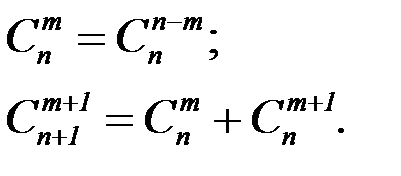
Число всех подмножеств множества, состоящего из n элементов, равно 2ⁿ:

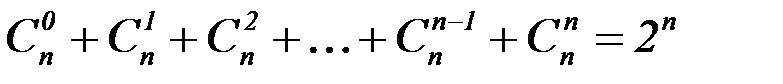
Числа размещений, перестановок и сочетаний связаны равенством:

.

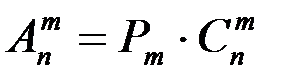Теперь рассмотрим основные правила комбинаторики.

Правило сложения: Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект B может быть выбран n способами, то выбрать либо A, либо B можно (m + n) способами.

Пример: Сколькими способами из колоды, содержащей 36 карт, можно выбрать туза или пиковую даму?

Решение: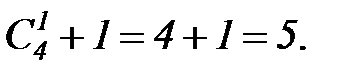

Заметим, что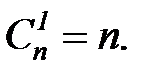

Правило произведения: Если объект A можно выбрать из совокупности объектов m способами и, после каждого такого выбора, объект B можно выбрать n способами, то пара объектов (A, B) в указанном порядке может быть выбрана m·n способами.

Пример: Из пункта А в пункт В можно добраться тремя способами, из пункта В в пункт С можно добраться двумя способами, а из пункта С в пункт D можно добраться четырьмя способами. Сколькими способами можно добраться из пункта A в пункт D?

Решение: Из пункта A в пункт D можно добраться 3·2·4= 24 способами.

Пример: Сколькими способами можно распределить золотую, серебряную и бронзовую медали между шестнадцатью претендентами?

Решение: Решить эту задачу можно двумя способами: по правилу произведения 16·15·14 = 3360, или используя формулу для размещений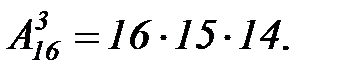

Дата добавления: 2014-12-27