
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частные простые формы кристаллов без единичного направления
|
|
|
|
С единичным направлением (исходная грань (h k 0)).
Частные простые формы кристаллов
| № фор-мы | Группа | Число граней | Много-гранник | Индексы граней |
| См.№1 | 1, m | моноэдр | (h k 0) | |
| См.№2 | 2, 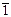 , 2/m, mmm, mm2 , 2/m, mmm, mm2
| пинакоид | ± (hk0) | |
| См.№33 | 3, 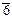 , ,
| тригональ-ная призма | (éh k i û 0) | |
| См.№34 | 4, 4/m, 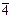
| тетрагональ-ная призма | 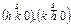
| |
| См.№35 | 6,  , 6/m , 6/m
| гексагона-льная призма | (± é hkiû 0) | |
32,3m, 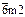
| дитригона-льная призма | 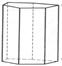 ({ hki}0)
({ hki}0)
| ||
4mm, 422, 4/mmm, 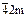
| дитетраго-нальная призма | 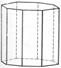
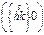
| ||
6mm, 622,  , 6/mmm , 6/mmm
| дигексаго-нальная призма |  (± é h k i û 0) и (±
é h i k û 0)
(± é h k i û 0) и (±
é h i k û 0)
|
Таблица 1.5
| № фор-мы | Индексы исходной плоскости | Группа | Число граней | Много-гранник | Индексы граней |
| (h 0 0) | 23, m3,  , 432, m3m , 432, m3m
| куб | 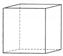
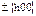
| ||
| (h h 0) | 23, m3, 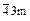 ,
m3m ,
m3m
| ромбодо-декаэдр | 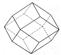

| ||
| (h 0 0) | 23,m3 | пентагон-додекаэдр |  é
é 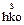 û û
| ||
| (hk0) |  432,
m3m
432,
m3m
| тетрагек-саэдр | 

| ||
| (hhh) | 23,
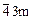
| тетраэдр | 
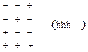
| ||
| (hhh) | m3, 432, m3m | октаэдр | 

| ||
| (hhl) h<1 | 23,
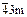
| тригонтри-тетраэдр | 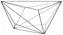

| ||
| (hhl) h>1 | 23,
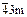
| тетрагон- тритетраэдр | 

| ||
| (hhl) h<1 | m3, 432, m3m | тригон- триоктаэдр | 

| ||
| (hhl) h>1 | m3, 432, m3m | тетрагон- триоктаэдр | 

|
Рассмотрим фигуру, полученную при сечении полиэдров, соответствующих простым формам кристаллов без единичного направления, координатной плоскость, например, Z=0. Легко убедиться, что при  в сечении лежит дитерагон, а при
в сечении лежит дитерагон, а при  - тетрагон. Очевидно, что это может выполняться лишь при различии полиэдров для условий
- тетрагон. Очевидно, что это может выполняться лишь при различии полиэдров для условий 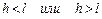 .
.
Монокристаллы с различными размерами не обязательно ограняются плоскостями одной формы. Например, для группы m3, 432, m3m возможно сочетание граней октаэдра и граней куба. Кристалл имеет форму кубоктаэдра, которая не является простой, ибо ее грани образуют два семейства симметрично связанных друг с другом плоскостей. Грани кубоктаэдра имеют индексы  , где k и h принимают произвольные значения, но так, чтобы грани октаэдра и куба не пересекались.
, где k и h принимают произвольные значения, но так, чтобы грани октаэдра и куба не пересекались.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 664; Нарушение авторских прав?; Мы поможем в написании вашей работы!