Шаровые упаковки как модели многоатомных структур

В общем случае шаровых упаковок может быть бесчисленное множество, но для атомов, с учетом их взаимодействия друг с другом, число таких упаковок не столь велико, особенно для атомов одного сорта. Если атом моделируется шаром, то следует говорить об изодесмичности межатомных связей. При выполнении этих условий коэффициент упаковки будет наибольшим. Для атомных шаровых упаковок, с учетом того, что при дальнейшем росте должен сформироваться макрокристалл с определенной симметрией [52], при описании атомных плотнейших упаковок рассматриваются две основные возможности.

На плоский слой плотнейшей шаровой упаковки (рис. 1.37) можно наложить второй аналогичный слой.

Рисунок 1.37 – Плотнейшая плоская шаровая упаковка

При этом атомы второго слоя находятся над пустотами между тремя шарами первого слоя. Это показано на рис. 1.38, на котором для большей наглядности шары немного раздвинуты [51].

При наложении третьего слоя шаров возможны два варианта. В первом варианте каждый шар третьего слоя лежит на трех шарах второго слоя таким образом, что под шаром третьего слоя нет шара в первом слое. Во втором – каждый шар третьего слоя тоже лежит на трех шарах второго слоя, но под каждым шаром третьего слоя оказывается шар в первом слое.

В обоих вариантах коэффициент компактности одинаков и равен К=0,741. Одинаковы у них и координационные числа, равные 12. Если шаровым слоям с различными конфигурациями атомов относительно прилегающих к ним слоев давать обозначения, то упаковка по первому варианту имеет вид …АВСАВС…, а по второму – …АВАВАВ…. Упаковки по первому варианту формируют гранецентрированные кубические (ГЦК) решетки, по второму – гексагональные плотные упаковки (ГПУ), которые представлены на рис. 1.39.

Рисунок 1.38 – Укладка второго слоя шаров в плотнейшей упаковке

Кроме указанных упаковок возможны и другие, с меньшими коэффициентами компактности. Среди упаковок, встречающихся у кристаллических моноатомных веществ, следует назвать объемно-центрированную (ОЦК) решетку, в основе которой лежит плоский шаровой слой, у которого центры шаров образуют квадратную сетку (слой А на рис. 1.40).

В пустотах между четырьмя шарами слоя А располагаются шары второго слоя (слой В, рис. 1.40). Центры этих шаров также образуют квадратную сетку. Шары третьего слоя повторяют слой А. Кристаллы с решеткой ОЦК характеризуются коэффициентом компактности, равным К=0,680. Если атомы второго слоя расположены точно над атомами слоя А, то создается примитивная кубическая упаковка (ПКУ) с коэффициентом компактности, равным К=0,524. Решетки типа ПКУ у моноатомных структур не встречаются, но они возможны у некоторых молекулярных (то есть многоатомных) кристаллов.

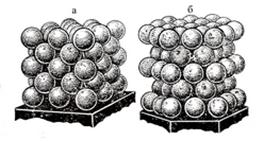
Рисунок 1.39 – Плотнейшие упаковки шаров по кубическому (а) и гексагональному (б) законам [3]

Рисунок 1.20 – Схема образования объемно-центрированной упаковки

В таблицах 1.6, 1.7, 1.8 приведены характеристики решеток металлов ГЦК-, ГПУ- и ОЦК-типов.

Таблица 1.6

Кристаллы с ГЦК-решеткой. Пространственная группа Fm3m, z*=4, КЧ*=12

Элемент	a Å (T=300K)	r Å	ρ г/см^3
Актиний	5,311	1,88	10,07
Алюминий	4,04955	1,43	2,698
Америций	4,894	1,73	13,14
γ-Железо	3,6467	1,29	7,648
Золото	4,07832	1,44	19,303
Иридий	3,8368	1,35	22,650
α-Иттербий	5,4862	1,940	6,959
α-Кальций	5,582	1,97	1,540
β-Кобальт	3,5440	1,26	8,720
β-Лантан	5,285	1,87	6,186
Литий	4,379	1,56	0,540
γ-Марганец	3,855	1,36	6,368
Медь	3,6147	1,275	8,936
Никель	3,5238	1,25	8,908
Палладий	3,89069	1,37	12,027
Платина	3,9238	1,385	21,447
δ-Плутоний	4,6370	1,64	15,92
Родий	3,8044	1,34	12,414
Свинец	4,9500	1,75	11,339
Серебро	4,08591	1,44	10,499
α-Стронций	6,0847	2,15	2,578

Продолжение таблицы 1.6

α-Торий	5,0843	1,79	11,724
α-Церий	4,85	1,71	8,23
γ-Церий	5,1612	1,825	6,768

* z – число атомов на ячейку, КЧ – координационное число, а – параметр ячейки, r – радиус атома, ρ – плотность.

Таблица 1.7

Кристаллы с ГПУ-решеткой. Пространственная группа С 6/mmm, z=2, КЧ=12, а, с – периоды решетки

Элемент	a Å	с Å	с/а	r* Å	ρ г/см^3
Бериллий	2,2853	3,5829	1,568	2,22	2,28	1,845
α-Гадолиний	3,6360	5,7826	1,590	3,57	3,64	7,895
α-Гафний	3,1946	5,0510	1,581	3,12	3,19	13,25
Гольмий	3,5773	5,6158	1,570	3,48	3,58	8,803
Диспрозий	3,5903	5,6475	1,573	3,50	3,59	8,536
α-Иттрий	3,6474	5,7306	1,571	3,54	3,65	4,472
Кадмий	2,9787	5,6166	1,886	2,98	3,29
α-Кобальт	2,5074	4,0699	1,623	2,49	2,51
α-Лантан	3,770	12,159	3,225	3,73	3,77	6,162
Литий	3,111	5,093	1,637	3,10	3.10	0,579
Лютеций	3,5031	5,5509	1,585	3,43	3,50	9,740
Магний	2,20928	5,21023	1,624	3,19	3,20	1,738
Натрий	3,767	6,154	1,634	3,77	3,77
α-Неодим	3,6579	11,7992	3,226	3,62	3,66	7,54
Осмий	2,7353	4,3191	1,579	2,67	2,74
α-Празеодим	3,6725	11,8354	3,223	3,63	3,67	7,004
Рений	2,760	4,458	1,615	2,74	2,76	21,04
Рутений	2,7057	4,2815	1,582	2,64	2,71
α-Самарий	3,621	26,25	7,241	3,59	3,63
α-Скандий	3,3090	5,2733	1,594	3,20	3,25	2,985
β-Стронций	4,319	7,071	1,635	4,31	4,31
α-Талий	3,4564	5,5247	1,598	3,40	3,46
α-Тербий	3,6010	5,6936	1,581	3,52	3,60	8,272
Технеций	2,735	4,388	1,604	2,70	2,73	11,497
α-Титан	2,9504	4,6833	1,587	2,89	2,95	4,505
Тулий	3,5375	5,5546	1,570	3,44	3,54	9,332
Цинк	2,66466	4,9469	1,856	2,66	2,91
α-Цирконий	3,2312	5,1477	1,593	3,17	3,23	6,565
Эрбий	3,5588	5,5874	1,570	3,46	3,56	9,051

*Указана анизотропия атомных размеров: левое значение r – в плоскости 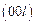, правое – вдоль .

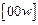На первый взгляд может показаться, что модель шаровых упаковок является лишь грубым приближением для описания решеток многоэлектронных атомов, так как сферической симметрией обладают лишь электронные s-орбитали, которые имеют значения квантовых чисел l и m, равные нулю [52]. Однако, во-первых, многие атомы металлов, переходя в ионные состояния, на внешней оболочке имеют именно s-состояния электронов. А, во-вторых, даже при невыполнении этого условия, например, для металлов из средней области периода таблицы Д.И. Менделеева, вследствие гибридизации электронных орбиталей электронная конфигурация атома обоснованно может моделироваться жестким шаром, то есть обладает сферической симметрией [41, 52].

Таблица 1.8

Кристаллы с ОЦК-решеткой. Пространственная группа Jm3m, z=2, КЧ=12

Элемент	a Å (T=300K)	r Å	ρ г/см^3
Барий	5,019	4,352	3,607
Ванадий	3,0258	2,632	6,015
Вольфрам	3,1651	2,748	19,25
β-Гадолиний	4,06	3,62	7,80

Продолжение таблицы 1.8

β-Галий	3,545	3,07	13,30
Европий	4,5820	4,084	5,245
α-Железо	2,86645	2,482	7,88
β-Иттрий	3,90	3,66	4,25
β-Иттрий (2)	4,45	3,96	6,52
Калий	5,344	4,626	0,8517
γ-Лантан	4,26	3,80	5,97
Литий	3,5093	3,036	0,5326
δ-Марганец	3,075	2,66	6,27
Молибден	3,1474	2,724	10,22
Натрий	4,2906	3,714	0,9660
β-Неодим	4,13	3,68	6,80
Ниобий	3,3004	2,858	8,581
β-Празеодим	4,13	3,68	6,64
Рубидий	5,710	4,942	0,5327
β-Самарий	4,07	3,62	7,40
β-Таллий	3,882	3,352	11,60
Тантал	3,3029	2,860	16,671
β-Титан	3,065	2,864	5,52
γ-Уран	3,528	3,052	18,06
Хром	2,8849	2,498	7,19
Цезий	6,079	5,264	0,9645
δ-Церий	4,11	3,66	6,67
β-Цирконий	3,6090	3,124	6,406

В-третьих, справедливость модели шаровых упаковок для металлов подтверждается экспериментальными результатами, представленными в табл. 1.6-1.8.

Дата добавления: 2014-12-27