Фуллереноподобные формы нанокристаллов

Возникновение частиц с габитусами некристаллографических симметрий (оси 5 или 10) вытекает из принципов классической кристаллографии [45-51] и соответствует правилам построения шаровых установок. В то же время эти правила ограничивают число возможных внешних форм с осями, порядки которых отличаются от кристаллографических. Интерес к таким формам особенно возрос после открытия квазикристаллов и фуллеренов [54-56]. Анализ структуры фуллеренов логично начать с ГПУ-решетки, которая, строго говоря, не является решеткой в математическом смысле, так как невозможно построить параллелепипед с осью шестого порядка. В работе [47] показано, что гексагональную упаковку можно рассматривать как трехмерную проекцию четырехмерной кубической решетки. Матрица-генератор группы вращения вокруг оси 6, совпадающей с осью t в ортогональной системе координат xyzt, имеет вид

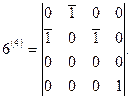(1.21)

Квазикристаллы, получаемые при резком охлаждении расплава, описываются группой вращения в 6-тимерном пространстве при матрице-генераторе, определяющей повороты вокруг осей 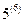и [57, 58].

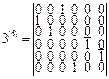, . (1.22)

По аналогии с гексагональными и квазикристаллическими структурами матрицы с элементами 0, ±1, причем ±1 в каждой строке и столбце встречаются один раз, могут быть записаны для пространства любой размерности. В краткой записи этих матриц надо указать номера элементов, равных ±1 с указанием знака. Например, матрицы (1.21) и (1.22) в виде матрицы-строки 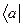и матрицы-столбца 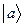(для сокращения объема записи 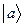приведены строкой) имеют вид

. (1.23)

Свойства матриц и при описания многомерных симметрий рассмотрены в работе [58]. Там же показано, что группа 5 может быть описана в 3-хмерном пространстве матрицей-генератором

, (1.24)

где 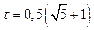– «золотое отношение».

Для описания точечных групп пента- и декагональной (оси 5 и 10) симметрий необходимо вместо кристаллических решеток [49] брать, так называемые, обобщенные решетки (ОР). 2-х мерные ОР известны как сетки Пенроуза. Матрица (6) описывает локальную симметрию, то есть ось 5 в структуре единственная. Для описания 3-хмерных сеток Пенроуза, то есть для 3D-ОР группы 5, ее матричное представление имеет вид:

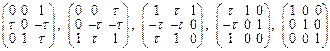. (1.25)

Следовательно, объекты с некристаллографической симметрией могут быть описаны на основе ОР теми же методами, что и применяемые в классической кристаллографии.

На рис. 1.45 приведены формы фуллеренов с различными числами атомов углерода, которые совпадают с результатами экспериментальных исследований [59].

Рисунок 1.45 – Модели фуллеренов, полученные в модели обобщенных решеток: a – C₆₀, b – C₇₂, с – С₈₀, d – C₁₂₀, e – C₁₃₂, f – C₁₄₀

Примеры фуллереноподобных структур, которые получены на основе метода ОР и которые могут соответствовать габитусам наночастиц, приведены на рис. 10. На этом рисунке описаны и формы, и число полигонов, образующих грани фуллереноподобного полиэдра [60, 61].

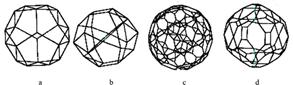
Рисунок 1.46– Фуллереноподобные полиэдры, полученные на основе трехмерных обобщенных решеток. Форма и число граней: a – 6 пг, 18 трг; b - 6 пг, 6 тетрг, 18 трг; с – 14ддг, 12 дг, 24 пг, 168‑тетрг, 120 трг; d – 8 нг, 42 тетрг. Сокращения: ддг – додекагон; дг – декагон; нг – наногон; пг – пентагон, тетрг – тетрагон; трг - тригон

Следовательно, фуллерены, квазикристаллы и в целом наночастицы, полученные путем выращивания вокруг отдельного атома или группы атомов, характеризуются габитусами, которые строятся на основе регулярных обобщенных решеток. В этом случае объясняется появление фуллереноподобных полиэдров с гранями, точечная симметрия которых отличается от кристаллографической, а сама частица может иметь оси вращения 5, 10 или других порядков.

Дата добавления: 2014-12-27