
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правильные формы кристаллов и их описание
|
|
|
|
Одно из определений кристалла гласит: «Кристаллами называются природные, искусственные или синтетические объекты, которые имеют естественную огранку, то есть их габитус (внешняя форма) является многогранником (полиэдром)». Сама форма этих многогранников может быть весьма разнообразной: на рис. 1.31 в качестве примера приведена форма монокристаллов пиропа 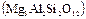 , который, наряду с упоминавшимся ранее гроссуляром, а также с альмандином
, который, наряду с упоминавшимся ранее гроссуляром, а также с альмандином 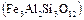 , спессартином
, спессартином 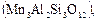 уваровитом
уваровитом 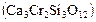 и андрадитом
и андрадитом 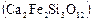 образует изоструктурную группу минералов, называемых гранатами. Поэтому габитусные полиэдры, приведенные на рис. 1.31 встречаются не только у пиропа, но и у других разновидностей группы граната. Все эти кристаллы относятся к кубической сингонии. Их ячейка – объемно-центрированная, пространственная группа Ia3d, число формульных единиц равно 8, период решетки лежит в интервале 11,46¸12,05 Ǻ.
образует изоструктурную группу минералов, называемых гранатами. Поэтому габитусные полиэдры, приведенные на рис. 1.31 встречаются не только у пиропа, но и у других разновидностей группы граната. Все эти кристаллы относятся к кубической сингонии. Их ячейка – объемно-центрированная, пространственная группа Ia3d, число формульных единиц равно 8, период решетки лежит в интервале 11,46¸12,05 Ǻ.
Кристаллы – это атомно-молекулярные системы с регулярным вдоль любого направления расположением гомологичных (кристаллохимические тождественных) точек. Структура решетки, точнее, решеточное строение кристалла, обуславливает рентгеновскую дифракцию на этих объектах, что позволяет определять межплоскостные расстояния кристаллохимических плоскостей. Для этого необходимо определить угол j между дифракционным (рассеянным) лучом и направлением первичного луча (рис. 1.32), а затем, зная длину волны рентгеновского излучения 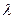 , можно рассчитать межплоскостное расстояние dºd/n (здесь n – целое число) по формуле
, можно рассчитать межплоскостное расстояние dºd/n (здесь n – целое число) по формуле
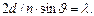 (1.12)
(1.12)
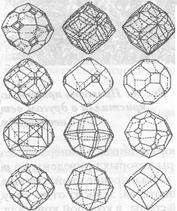
Рисунок 1.31 – Природные формы кристаллов граната
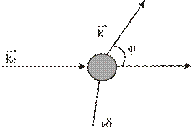
Рисунок 1.32 – Схема рассеяния рентгеновского излучения
В этой формуле угол 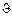 называется бреговским, причем
называется бреговским, причем 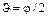 , а сама формула – это формула Вульфа-Брэггов (в честь Российского ученого Г.В. Вульфа и английских ученых У.Г. Брэгга и У.Л. Брэгга).
, а сама формула – это формула Вульфа-Брэггов (в честь Российского ученого Г.В. Вульфа и английских ученых У.Г. Брэгга и У.Л. Брэгга).
Положение плоскости в кристаллографическом барке описывается тремя целыми числами 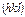 (круглые скобки обязательны), которые называются кристаллографическими индексами (обычно, просто индексами) и определяются следующим образом.
(круглые скобки обязательны), которые называются кристаллографическими индексами (обычно, просто индексами) и определяются следующим образом.
В кристалле плоскости с одинаковыми 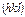 параллельны друг другу и углы ячейки вместе или по отдельности попадают на одну из этих плоскостей (в пакете), то (см. рис. 1.33) при любых
параллельны друг другу и углы ячейки вместе или по отдельности попадают на одну из этих плоскостей (в пакете), то (см. рис. 1.33) при любых 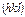 одна из плоскостей этого пакета пройдет через начало координатной кристаллографической системы и через точки x=a, y=b, z=c, причем эти точки в общем случае лежат на разных плоскостях этого пакета. То есть плоскость может проходить через точку х=а, но при этом через другие точки (y=b, z=c) будет проходить не эта, а другая плоскость из плоскостей
одна из плоскостей этого пакета пройдет через начало координатной кристаллографической системы и через точки x=a, y=b, z=c, причем эти точки в общем случае лежат на разных плоскостях этого пакета. То есть плоскость может проходить через точку х=а, но при этом через другие точки (y=b, z=c) будет проходить не эта, а другая плоскость из плоскостей 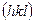 . Рассмотрим плоскость, отсекающую от координатных осей кристаллографической системы отрезки
. Рассмотрим плоскость, отсекающую от координатных осей кристаллографической системы отрезки 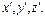 Очевидно, что
Очевидно, что 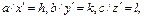 где hkl – целые числа. Они то и определяют индексы плоскости. Следовательно, если заданы
где hkl – целые числа. Они то и определяют индексы плоскости. Следовательно, если заданы 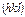 , то эта плоскость от координатных осей кристаллографической системы отсекает отрезки a/h, b/k, c/ l, и параллельно этой плоскости проходят множество других, кристаллографически тождественных данной, причем обязательно одна из плоскостей этой совокупности пройдет через начало координат. Расстояние от начала координат до ближайшей к нему плоскости с координатами
, то эта плоскость от координатных осей кристаллографической системы отсекает отрезки a/h, b/k, c/ l, и параллельно этой плоскости проходят множество других, кристаллографически тождественных данной, причем обязательно одна из плоскостей этой совокупности пройдет через начало координат. Расстояние от начала координат до ближайшей к нему плоскости с координатами 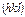 и есть межплоскостное расстояние.
и есть межплоскостное расстояние.
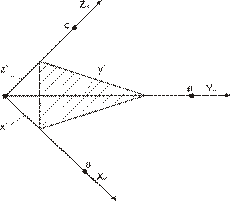
Рисунок 1.33 – К определению индексов плоскости (hkl)
Для исследования структуры кристалла, наряду с рентгеновским излучением можно использовать электронные или нейтронные пучки. Для получения электронного пучка электроны разгоняются полем с разностью потенциалов U. Схема получения картины электронной дифракции та же, что и для рентгеновских лучей (рис. 1.32).
Длина волны электронов в пучке равна
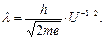 (1.13)
(1.13)
После подстановки в это уравнение значений постоянной Планка (h) массы и заряда электрона (me) и значения U (В) длина волны l 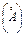 определяется как
определяется как
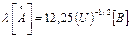 . (1.14)
. (1.14)
Исследования структуры кристаллов дифракционными методами (рентгенография, электронография, нейронография) характеризуются достаточно выраженной трехэтапной схемой [41]. На первом этапе основное внимание уделяют анализу положения рентгеновских рефлексов, то есть основным экспериментальным параметром является брегговский угол 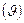 . Основным уравнением первого этапа структурного анализа являются уравнение Вульфа-Брэггов (см. (1.12)), а также квадратичная формула:
. Основным уравнением первого этапа структурного анализа являются уравнение Вульфа-Брэггов (см. (1.12)), а также квадратичная формула:
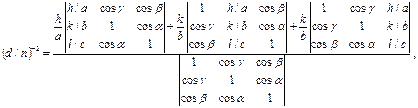 (1.15)
(1.15)
где (a, b, c) – линейные, 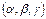 – угловые параметры кристалла,
– угловые параметры кристалла, 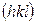 – кристаллографические индексы плоскости, от которой получен рефлекс.
– кристаллографические индексы плоскости, от которой получен рефлекс.
На втором этапе решают задачу по определению структуры кристалла, то есть взаимного расположения атомов, которое описывается набором координат атомов, входящих в ячейку кристалла. Основной формулой этот этапа является
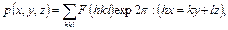 (1.16)
(1.16)
где 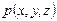 – функция электронной плотности,
– функция электронной плотности, 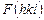 – структурная амплитуда, определяемая интенсивности рефлекса
– структурная амплитуда, определяемая интенсивности рефлекса 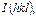 причем
причем
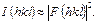 (1.17)
(1.17)
Так как 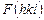 в общем случае является комплексной величиной, то ее определение сопряжено с довольно существенными трудностями, известными под названием «фазовая проблема». Это объясняет наличие трех методов в структурном анализе: «проб и ошибок», Фурье и Паттерсона. На этом этапе структурных исследований определяют, так называемую, идеальную структурную модель, в которой приведены взаиморасположения атомов при отсутствии любых примесей и других дефектов, то есть в идеальной модели используют принцип абсолютной регулярности, соответствующий понятию бесконечно дальнего порядка.
в общем случае является комплексной величиной, то ее определение сопряжено с довольно существенными трудностями, известными под названием «фазовая проблема». Это объясняет наличие трех методов в структурном анализе: «проб и ошибок», Фурье и Паттерсона. На этом этапе структурных исследований определяют, так называемую, идеальную структурную модель, в которой приведены взаиморасположения атомов при отсутствии любых примесей и других дефектов, то есть в идеальной модели используют принцип абсолютной регулярности, соответствующий понятию бесконечно дальнего порядка.
Задачи третьего этапа связаны с определением особенностей изменений структуры в конкретном «кристаллическом индивидууме» в зависимости от его состава, дефектности, внешних воздействий (термическая обработка, деформирование, облучение, действие полей и т. д.). Основного, единого метода для решения этих задач нет, но известно, что необходимая информация может быть получена не только из анализа положений и интенсивностей рассеяния (модуляции фона).
Кристаллические образцы, предназначенные для структурных исследований, могут быть монокристаллами (это основное требование для второго этапа) или поликристаллами (первый и третий этапы). При исследовании поликристаллов, когда размеры кристаллов достаточно маленькие, наблюдается усиление рентгеновских рефлексов. Следовательно, размеры частиц в порошке 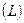 можно определить рентгеновскими методами. Расчет L осуществляют по формуле Шеррера
можно определить рентгеновскими методами. Расчет L осуществляют по формуле Шеррера
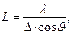 (1.18)
(1.18)
где 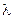 – длина волны рентгеновского излучения,
– длина волны рентгеновского излучения, 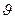 – брэгговский угол, определяемый по максимальной интенсивности рефлекса,
– брэгговский угол, определяемый по максимальной интенсивности рефлекса, 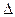 – угловая полуширина рефлекса, т. е. угловая ширина на половине высоты рефлекса.
– угловая полуширина рефлекса, т. е. угловая ширина на половине высоты рефлекса.
Как видно из рис. 1.31, формы кристаллов одного и того же вещества могут быть достаточно различными. Однако, каждая из плоских граней может быть описана индексами 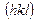 параллельной этой грани кристаллографической плоскости. Если кристалл ограничен только плоскостями, связанными между собой группой точечной линии (С), то полиэдр, ограненный этими плоскостями, называется правильной формой кристалла. Следовательно, для получения индексов граней правильных форм кристаллов – (
параллельной этой грани кристаллографической плоскости. Если кристалл ограничен только плоскостями, связанными между собой группой точечной линии (С), то полиэдр, ограненный этими плоскостями, называется правильной формой кристалла. Следовательно, для получения индексов граней правильных форм кристаллов – (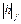 ) – необходимо использовать формулу
) – необходимо использовать формулу 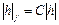 , где
, где 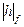 и
и 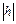 – матрицы-столбцы индексов граней правильной формы и исходной грани соответственно.
– матрицы-столбцы индексов граней правильной формы и исходной грани соответственно.
Если один или два индекса исходной грани равны нулю, или взаиморавны два или три индекса, полученная форма является частной. Индексы граней общих и частных простых форм кристаллов различных точечных групп, а также названия габитусных полиэдров приведены в табл. 1.2-1.5. Число граней простой формы равно фактору повторяемости при поликристаллических рентгенодифракционных исследованиях. При записи индексов граней правильных форм использованы следующие сокращения. Если порядок индексов не меняется, то над ними или перед ними указаны лишь их знаки. Например, группа 2/m имеет форму 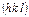 ,
, 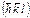 ,
, 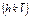 ,
, 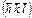 и в краткой форме записывается в виде
и в краткой форме записывается в виде 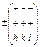 или
или 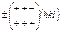 . Запись
. Запись 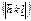 означает плоскости с циклической перестановкой индексов, т.е.
означает плоскости с циклической перестановкой индексов, т.е. 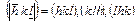 . Запись
. Запись 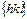 означает перестановку индексов
означает перестановку индексов 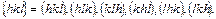 Если необходимо осуществить перестановку знаков, над индексами ставится символ S. Например, группа 4mm имеет форму
Если необходимо осуществить перестановку знаков, над индексами ставится символ S. Например, группа 4mm имеет форму 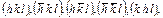
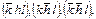 что тождественно записи
что тождественно записи 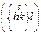 .
.
Таблица 1.2
Общие простые формы кристаллов и кристаллографические индексы их граней (hkl)
| № | ТГ(n) | Многогранник | (hkl)ф |
| 1(1) | моноэдр (педион) | (hkl) | |
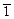 (2) (2)
| пинакоид | ± (hkl) | |
| 2(2) | диэдр (осевой) | 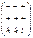
| |
| m(2) | диэдр планальный (плакательный) | 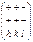
| |
| 2/m(4) | ромбическая призма | 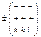
| |
| 222(4) | ромботетраэдр | 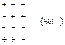
| |
| mm2(4) | ромбическая пирамида | 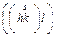
| |
| mmm(8) | ромбическая бипирамида | 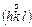
| |
| 3(3) | тригональная пирамида | R) (é hkl û) H) (é hki û l) | |
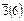
| ромбоэдр | R) (± é hklû) H) (± é hki û l) | |
| 3m(6) | дитригональная пирамида | R) {hkl} H) (± éhkiûl) | |
| 32(6) | тригональный трапецоэдр | R) (± é hklû) H) (é hki û ± l) | |
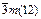
| тригональный скаленоэдр | H) ± {hkl}
H) (é hki û l) и (éhikû 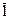 ) )
| |
| 4(4) | тетрагональная пирамида | (± (hk)l) и (± 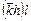 ) )
| |
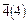
| тетрагональный тетраэдр | (± (hk)l) и (± 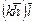 ) )
| |
| 4/m(8) | тетрагональная бипирамида | ((hk) ± l) и (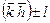 ) )
| |
| 4mm(8) | дитетрагональ- ная пирамида | 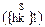
| |
| 422(8) | тетрагональный трапецоид | (± (hk)l), (± 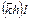 ) )
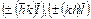
| |
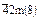
| тетрагональный скаленоэдр | 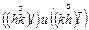
| |
| 4/mmm (16) | дитертраго-нальная бипирамида | 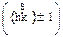
| |
| 6(6) | гексагональная пирамида | (± é hki û l) | |
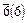
| тригональная бипирамида | (é hki û ± l) | |
| 6/m(12) | гексагональная бипирамида | (±éhkiû 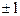 ) )
| |
| 622(12) | гексагональный трапецоид | (±éhkiû 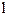 ), (±éhkiû ), (±éhkiû 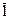 ) )
| |
| 6mm(12) | дигексагональная пирамида | (±{hki}l) | |
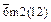
| дитригональная бипирамида | (éhkiû 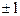 ) и (é ) и (é 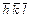 û û 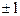 ) ) 
| |
| 6/mmm(24) | дигексагональ-ная бипирамида | ({hki}± l) | |
| 23(12) | пентагон-тритетраэдр | 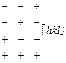
| |
| m3(24) | дидодэкаэдр | (é 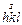 û) û)
| |
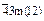
| гексоктаэдр |  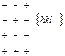
| |
| 432(24) | пентагон-триоктаэдр | 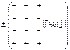
| |
| m3m(48) | гексатетраэдр | 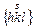
|
** ТГ – точечная группа в международном обозначении и ее порядок (п), которому равно число граней. Сингонии отделены друг от друга горизонтальными линиями
Для гексагональных и тригональных кристаллов в гексагональной установке (Н -установке) осей вводится индекс i=-h-k. В этом случае, например, записи ([hki]l) для группы 3 и ({hki}l) для группы 3m означают соответственно (h,k,(-h-k),l), (h,(-h-k),k,l) ((-h-k),k h l) и (h,k,(-h-k)l, (h,(-h-k),k,l), (k,h(-k-h)l), (k,(-k-h),h,l), ((-h-k),h,k,l), ((-h-k)k,h,l).
Если в качестве исходной грани взять плоскость (0 0 l), то для полярных кристаллов с единичным направлением вдоль оси Z простая форма – моноэдр, для неполярных – пинакоид. В этом легко убедиться, если взять индексы граней соответствующих общих форм и подставить значения h=k=0.
В тригональных кристаллах при установке оси 3 параллельно [111] (R – установка) для получения пинакоида (группы 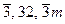 ) или моноэдра (группы 3, 3m) в качестве исходной необходимо взять плоскость (111).
) или моноэдра (группы 3, 3m) в качестве исходной необходимо взять плоскость (111).
Общие простые формы приведены на рис. 1.34 соответствующими многогранниками и индексами граней при исходной грани с индексами (hkl). Изображения многогранников общей правильной формы для всех 32 точечных групп приведены на рис. 1.34, причем эти многогранники будут сохранять свой вид для любых неравных друг другу hkl, но при этом могут меняться их геометрические размеры, например, будут увеличиваться или уменьшаться их высота для точечных групп с единичным направлением, которые относятся по всем сингониям, кроме кубической.
| Сингонии | М н о г о г р а н н и к и | ||||||
| Триклинная, моноклинная |  Моноэдр
педион
Моноэдр
педион
| 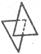 Пинакоид
Пинакоид
| 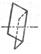 Диэдр осевой
Диэдр осевой
| 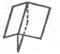 Диэдр безосный
Диэдр безосный
| 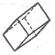 Призма
Призма
| ||
| Ромбическая |  Тетраэдр
Тетраэдр
| 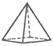 Пирамида
Пирамида
|  Бипирамида
Бипирамида
| ||||
| Тригональная | 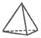 Пирамида
Пирамида
|  Ромбоэдр
Ромбоэдр
|  Трапецоэдр
Трапецоэдр
| 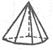 Дитириг. пирамида
Дитириг. пирамида
|  Скаленоэдр
Скаленоэдр
| ||
| Тетрагональная |  Пирамида
Пирамида
| 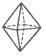 Бипирамида
Бипирамида
|  Трапецоэдр
Трапецоэдр
| 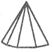 Дитетрагон пирамида
Дитетрагон пирамида
|  Дитетрагон бипирамида
Дитетрагон бипирамида
| 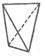 Тетраэдр
Тетраэдр
| 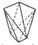 Скаленоэдр
Скаленоэдр
|
| Гексагональная | 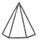 Пирамида
Пирамида
|  Бипирамида
Бипирамида
|  Трапецоэдр
Трапецоэдр
| 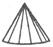 Дигексаген пирамида
Дигексаген пирамида
|  Дигексаген бипирамида
Дигексаген бипирамида
| 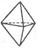 Тригональная бипирамида
Тригональная бипирамида
|  Дитригона-льная бипирамида
Дитригона-льная бипирамида
|
| Кубическая | 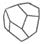 Пентаго-тритетра-эдр
Пентаго-тритетра-эдр
|  Дидодекаэдр
Дидодекаэдр
|  Пентагон-триоктаэдр
Пентагон-триоктаэдр
|  Гексатетра-эдр
Гексатетра-эдр
|  Гексоктаэдр
Гексоктаэдр
|
Рисунок 1.34 – Многогранники общих правильных форм кристаллов (таблица 1.2)
Реальные кристаллы могут иметь грани, относящиеся к разным формам, когда их грани соответствуют кристаллографическим плоскостям с различными индексами, что и приводит к различным формам одни и тех же кристаллов.Кроме того, на форму кристаллов влияют не только симметрия их решетки, но и характер взаимодействия между атомами. Если, например, в кристалле атомы расположены слоями, причем в пределах слоя межатомная связь намного сильнее, чем связь между слоями, как в кристаллах гранита и слюд, то, несмотря на их различные сингонии (графит относится к гексагональной, а слюда – к моноклинной сингонии), кристаллы у этих веществ имеют одинаковую форму тонких пластинок – чешуек. У этих кристаллов атомы в слоях связаны валентными силами, а межслоевое воздействие имеет Ван-дер-Ваальсову природу.
При диспергировании кристалла, когда поверхностные силы не играют существенную роль в формировании габитуса частицы, продукты диспергирования имеют форму полиэдров. Кристалл при его механическом дроблении ограничивается плоскостями с наибольшей ретикулярной плоскостью, то есть с наибольшим числом атомов на единицу поверхности.
На рис. 1.35 приведены формулы симметрий каждой из 32 точечных групп кристаллов, здесь же указан их симметрический комплект, а также международное обозначение точечной группы. Так как в теоретической физике, в структурной химии и в других разделах науки до сих пор сохраняется обозначения точечных групп по Шенфлису, то на рис. 1.36 приведены эти обозначения.
Если в качестве исходной плоскости для кристаллов с единичным направлением взят боковой пинакоид (плоскости (h 0 0) или (0 k 0)), то наряду с рассмотренным возникают некоторые новые простые формы, которые для кристаллов с единичным направлением приведены в табл. 1.3. Если правильная форма встречалась ранее, то указан ее номер в предыдущей таблице.
При исходной грани (0 k 0), когда 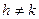 , возникают новые формы кристаллов с единичным направлением (табл. 1.4). Исходные грани типа (h 0 l), (0 k l) или (h h 0) для кристаллов с единичным направлением не приводят к возникновению новых форм.
, возникают новые формы кристаллов с единичным направлением (табл. 1.4). Исходные грани типа (h 0 l), (0 k l) или (h h 0) для кристаллов с единичным направлением не приводят к возникновению новых форм.
В кристаллах без единичного направления (кубическая сингония) наряду с общими простыми формами, возможны частные при исходных плоскостях: 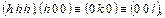
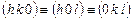 ,
, 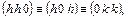 . Очевидно, что частные простые формы могут быть получены из общих простых форм кристаллов соответствующих точечных групп при подстановке индексов исходной грани частной формы.
. Очевидно, что частные простые формы могут быть получены из общих простых форм кристаллов соответствующих точечных групп при подстановке индексов исходной грани частной формы.

Рисунок 1.35 – Комплексы элементов симметрии 32 точечных групп, их обозначения по Шенфлису – международное.
Рисунок 1.36 – Пояснения к рис. 1.35
Таблица 1.3
Частные простые формы (грань (h 0 0))
| № фор-мы | Группа | Число граней | Много-гранник | Индексы граней |
| См.№1 | 1, m | моноэдр | (h 0 0) | |
| См.№2 | 2, 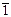 ,2/m,mm2,
222,mmm ,2/m,mm2,
222,mmm
| пинакоид | ± (± h 0 0) | |
| тригона-льная призма |  (é
(é 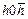 û 0) û 0)
| |||
4,4/m, 4mm, 422, 4/mmm,
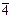 , , 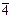 2m 2m
| тетраго-нальная призма |  (± éh 0û 0)
(± éh 0û 0)
| ||
6,  , 6m, 3m,
6mm, 32, 622, , 6m, 3m,
6mm, 32, 622,
 m, 6/mmm, m, 6/mmm,
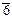 , , 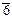 m2 m2
| гексаго-нальная призма |  (é
(é 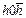 û l) û l)
|
Для тригональных кристаллов в табл. 1.3 и 1.4 приведена только гексагональная установка осей: 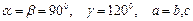 . Получить индексы граней чистых правильных форм тригональных кристаллов при R – установке координационных осей можно на основании табл. 1.2, взяв за исходную грань (hhh).
. Получить индексы граней чистых правильных форм тригональных кристаллов при R – установке координационных осей можно на основании табл. 1.2, взяв за исходную грань (hhh).
При исходной плоскости (h h l) в зависимости от величины индексов h и l полиэдры, изображающие простую форму кубических кристаллов имеют разный вид, хотя индексы граней формы одинаковы. Различие полиэдров при исходной плоскости (h k l) для случаев 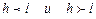 можно доказать, анализируя грани форм, приведенных в табл. 1.5 (см. № 44-47).
можно доказать, анализируя грани форм, приведенных в табл. 1.5 (см. № 44-47).
Таблица 1.4
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 2476; Нарушение авторских прав?; Мы поможем в написании вашей работы!