
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методологические подходы к описанию кристаллов
|
|
|
|
Модельные представления о структуре и габитусе наноразмерных частиц
При диспегировании кристаллов, начиная с размеров порядка долей миллиметра, форма их микрочастиц определяется в основном, особенностями их кристаллической структуры [41-44], т. е. их морфологическая симметрия соответствует точечной группы кристалла. Можно сделать предположение, что структура частицы соответствует структуре в объеме, равном этой частице в пределах бесконечного в физическом смысле кристалла. Следовательно, если 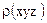 - структура кристалла, то кристаллическая структура частицы определяется условием [45]
- структура кристалла, то кристаллическая структура частицы определяется условием [45]
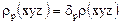 , (1.3)
, (1.3)
где 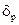 - фактор формы частицы, обладающий свойствами;
- фактор формы частицы, обладающий свойствами; 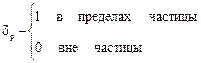 .
.
Точечная группа кристалла в кристаллофизическом пространстве (D) может быть представлена матрицами Эйлера [45, 46], которые в кристаллофизическом (декартовом) пространстве имеют вид:
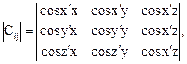 (1.4)
(1.4)
где x, y, z – исходное положение, а 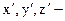 положение после выполнения точечного движения положения координатных осей.
положение после выполнения точечного движения положения координатных осей.
В общем случае кристаллографическая (КГ) система косоугольная. Ориентация осей этой системы в системе декартовой, обычно называемой кристаллофизической (КФ) приведена на рис. 1.22: оси 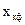 и
и 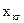 совпадают, ось
совпадают, ось 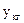 лежит в плоскости
лежит в плоскости 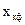 Угловые параметры КГ – системы указаны на рис. 1.22.
Угловые параметры КГ – системы указаны на рис. 1.22.
Для расчета индексов граней правильных форм используем матричное представление точечной группы кристалла в кристаллографическом пространстве (C), которое определяется по формуле 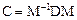 , где М и М-1 – прямой и обратный метрические тензоры решетки, имеющие в общем случае (триклинная решетка) вид [47, 48]:
, где М и М-1 – прямой и обратный метрические тензоры решетки, имеющие в общем случае (триклинная решетка) вид [47, 48]:
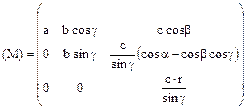 , (1.5)
, (1.5)
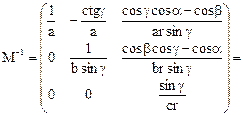
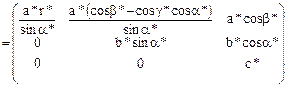 , (1.6)
, (1.6)
где 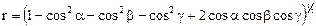 ,
,
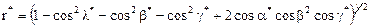 .
.
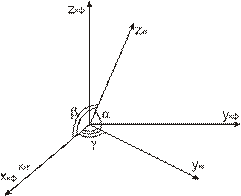
Рисунок 1.22 – Расположение кристаллографической системы (КГ) относительно осей кристаллофизической (КФ) системы.
Метрические тензоры прямой и обратной решеток характеризуют ячейку кристалла и позволяют описать симметрию решетки. Решетка – как трехмерная трансляция позволяет найти расположение гомологичных, т.е. тождественных в кристаллохимическом отношении точек в кристалле. Допустим, репер Бравэ описывается векторами 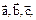 отсюда
отсюда 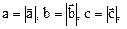 a=ë
a=ë 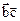 , b=ë
, b=ë 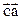 , g=ë
, g=ë 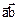 . Если имеется какая-то точка с координатами в репере Бравэ, о есть в кристаллографической системе координат, равными
. Если имеется какая-то точка с координатами в репере Бравэ, о есть в кристаллографической системе координат, равными  , то любая другая точка
, то любая другая точка  с координатами
с координатами
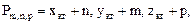 (1.7)
(1.7)
где m, n, p Î Z, кристаллохимически абсолютно тождественна точке Р, то есть
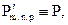
так как все эти точки связаны трехмерной трансляцией
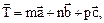 (1.8)
(1.8)
но в кристаллографической системе принято
 .
.
Для перехода от кристаллографической (КГ) к кристаллофизической (КФ) системе (то есть к декартовой системе координат) необходимо использовать условие:
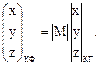 (1.9)
(1.9)
Для обратного перехода  надо взять условие:
надо взять условие:
 (1.10)
(1.10)
где 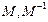 - прямой и обратный метрические тензоры решетки (см. (1.5),(1.6)).
- прямой и обратный метрические тензоры решетки (см. (1.5),(1.6)).
Структуру кристалла в структурной физике описывают различными способами, из которых наиболее употребляемые – табличный, графический, полиэдрический. Первый способ представлен таблицей, форма которой приведена на рис. 1.23. Коэффициенты заданы в репере Бравэ, т. е. 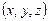 , и обычно из всей группы атомов, связанных симметрией, приводится координата только одного из них.
, и обычно из всей группы атомов, связанных симметрией, приводится координата только одного из них.

Рисунок 1.23 – Форма таблицы для описания структуры кристалла
Графическая форма представления структуры уже была приведена ранее для сфалерита (рис. 1.2). Обычно эта форма является развитием модели шаровых упаковок. На рис. 1.24 приведена модель шаровой упаковки минерала галлита (поваренная соль, NaCl). Отношения радиусов шаров, моделирующих 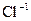 и
и 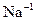 равно отношению ионных радиусов этих компонентов.
равно отношению ионных радиусов этих компонентов.

Рисунок 1.24 – Модель шаровой упаковки кристалла NaCl
Эта модель не позволяет увидеть всю ячейку, поэтому вместо шаров, моделирующих атомы (здесь ионы) можно указать положения их центров. В этом случае структура NaCl будет иметь вид, приведенный на рис. 1.25.
Видно, что ячейка галлита имеет кубическую форму с параметром а=5,93Ǻ. Эта структура может быть описана двумя одинаковыми связанными друг с другом решетками. Действительно, ионы хлора расположены в узлах и в центрах граней кубической ячейки, то есть ячейки принадлежат четыре иона хлора с КГ-координатами (000; ½, ½, 0; ½, 0, ½; ½, ½, 0), что соответствует кубической гранецентрированной ячейке. Ионы натрия расположены абсолютно аналогичным образом в такой же кубической гранецентрированной ячейке (F-типа), которая сдвинута относительно ячеек хлора на трансляцию (в КГ-системе)
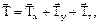 (1.11)
(1.11)
где 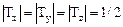 .
.
Ионы натрия имеют координаты: 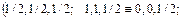
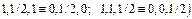 . То есть координаты
. То есть координаты  в структуре NaCl имеют значения
в структуре NaCl имеют значения 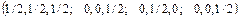 (см. рис. 1.25).
(см. рис. 1.25).
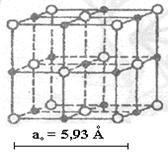
Рисунок 1.25 – Модель структуры NaCl, указывающая положения 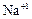 и
и 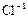 в ячейке
в ячейке
Если структура кристалла достаточно сложная, то для его снижения используют полиэдрическую модель. Принцип ее построения рассмотрим на примере NaCl.
Как следует из рис. 1.25, более мелкие катионы 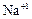 находятся в окружении шести анионов
находятся в окружении шести анионов 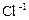 . Если соединить центры этих анионов, то будет получен октаэдр (рис. 1.26), а вся структура этого кристалла в этом случае представляет собой совокупность этих структурных полиэдров (рис. 1.27). На рис. 1.27 приведено два сорта октаэдров, в вершинах ионы хлора (октаэдр вокруг иона Na (1, 1, 1), то есть верхний правый) и с ионами натрия в вершинах октаэдров. Обычно выбирают полиэдры, построенные вокруг более мелких ионов, то есть, как правило – это полиэдры из анионов вокруг катионов.
. Если соединить центры этих анионов, то будет получен октаэдр (рис. 1.26), а вся структура этого кристалла в этом случае представляет собой совокупность этих структурных полиэдров (рис. 1.27). На рис. 1.27 приведено два сорта октаэдров, в вершинах ионы хлора (октаэдр вокруг иона Na (1, 1, 1), то есть верхний правый) и с ионами натрия в вершинах октаэдров. Обычно выбирают полиэдры, построенные вокруг более мелких ионов, то есть, как правило – это полиэдры из анионов вокруг катионов.
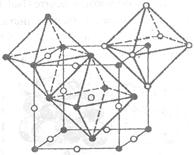
Рисунок 1.26 – Принцип построения полиэдрической модели NaCl. ● - Na, ○ - Cl
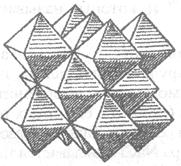
Рисунок 1.27 – Полиэдрическая модель структуры кристалла NaCl (минерал галлит)
Исключения возможны, если, например, катионы имеют размер больше, чем анионы. Возможно ситуация, как в приведенном примере, когда полиэдры и катионные и анионные создают один и тот же структурный мотив.
В качестве примера на рис. 1.28 представлена полиэдрическая модель одной из разновидностей граната, а именно, гроссуляра 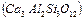 .
.
Кислородные тетраэдры расположены вокруг Si. Вокруг Al расположены кислородные октаэдры. Атомы Са находятся внутри полиэдра полученного из куба, у которого две противоположные грани повернуты относительно перпендикулярной к ним оси на 45 о. Такой полиэдр называется закрученным кубом (рис. 1.29).
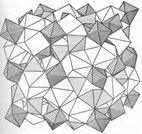
Рисунок 1.28 –Полиэдрическая модель кристаллической структуры гроссуляра

Рисунок 1.29 – Закрученный куб – кислородный полиэдр вокруг Са в гроссуляре (рис. 1.28)
Пример более сложной полиэдрической модели кристалла с достаточно большим числом атомов на ячейку приведен на рис. 1.30.

Рисунок 1.30 – Полиэдрическая модель зусманита 
Метод полиэдрических моделей описания структур кристаллов в ряде случаев может быть использован и для некристаллических объектов, например, стекол и, в отдельных случаях, жидкостей. Естественно, в этом случае взаимоориентация полиэдров не будет сохраняться, то есть решетчатая симметрия исчезнет, а для жидкостей эта модель позволяет описать только небольшие объемы вещества и показывает лишь усредненную взаимоориентацию структурных полиэдров, так как в некристаллических веществах дальнейший порядок отсутствует.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 777; Нарушение авторских прав?; Мы поможем в написании вашей работы!