Методические рекомендации к решению задач по теме плоское движение твердого тела

Угол наклона вектора абсолютного ускорения точки к расстоянию от этой точки до МЦУ не зависит от выбора точки тела, т.е. все ускорения точек одинаково наклонены к расстоянию от точки до МЦУ.

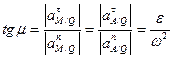(23)

в) Методы определения МЦУ.

1. Если ω = 0, а 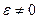, это означает, что 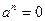, а 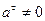и ускорение 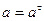, то МЦУ будет лежать на пересечении перпендикуляров к ускорениям двух точек (Рис.60).

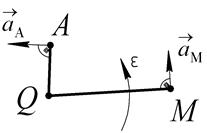
Рис. 60

2. Если 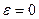, , 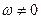то 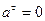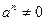и абсолютное ускорение 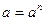, то ускорения всех точек плоской фигуры направлены к мгновенному центру ускорений и МЦУ будет лежать на пересечении самих ускорений двух точек (Рис.61).

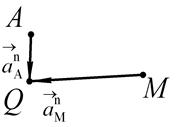
Рис. 61

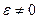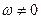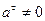
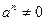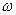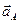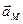Если , , то , то, кроме угловой скорости и углового ускорения E должны быть известны направления ускорений точек А и М – и , а также угол наклона вектораабсолютного ускорения точки к расстоянию от этой точки до МЦУ- 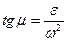или 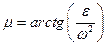; тогда МЦУ лежит на пересечении прямых проведенных под углом m к ускорениям (Рис.62).

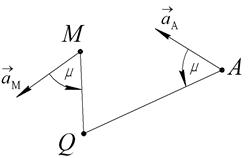
Рис. 62

4. Пусть известно ускорение какой-нибудь точки и по величине и по направлению (например точки А - 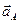), а также известно, что 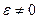, 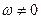. Определим 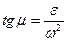и расстояние 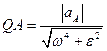; то есть МЦУ находится на расстоянии QA от точки А под углом m к ускорению 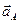(Рис.63).

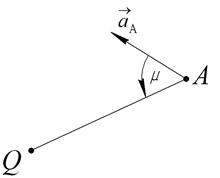
Рис. 63

5. Общий случай.

Известны ускорения двух точек А и М по величине и по направлению, известна длина отрезка АМ, но не известны угловая скорость 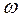и угловое ускорение 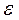. Необходимо определить положение мгновенного центра ускорений, а также угловую скорость и угловое ускорение звена АВ.

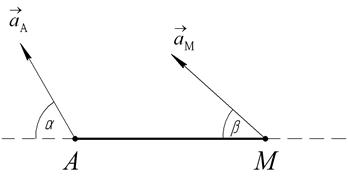
Рис. 64

Любую точку (А или М) берем за полюс. Будем считать, что точка А полюс. Тогда, ускорение точки М может быть определено с помощью формулы распределения ускорений (Рис.64):

;

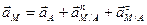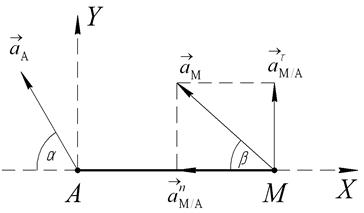
Рис. 65

Спроектируем это векторное равенство на координатные оси X и Y (Рис.65).

Получим:

- проекция на ось Х:

;

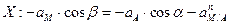Отсюда:

;

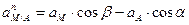Из этого выражения определим угловую скорость:

.

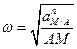- проекция на ось Y:

;

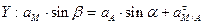Отсюда:

;

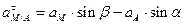Из этого выражения определим угловое ускорение:

,

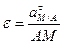а значит определяем .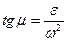

Откладываем под углом 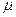отрезки к направлениям ускорени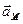й и 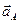. Пересечение этих прямых и является мгновенным центром ускорений Q (Рис.66).

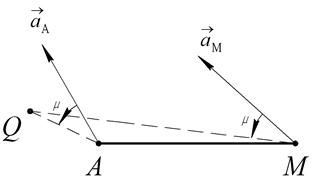
Рис. 66

6. Определение положения мгновенного центра ускорений в случае, когда ускорения точек плоской фигуры параллельны между собой.

Положение мгновенного центра ускорений – Q определяется в этом случае на основании следующего:

- ускорения точек пропорциональны длинам отрезков, соединяющих точки с МЦУ, то есть:

.

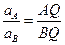- ускорения точек составляют с отрезками, соединяющими точки один и тот же угол:

.

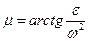Возможны несколько случаев:

1. Известны угловая скорость 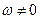, угловое ускорение 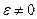, угол наклона вектораабсолютного ускорения точки к расстоянию от этой точки до МЦУострый, то есть изменяется в пределах .

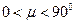Положение МЦУ в этом случае определяется построением, приведенным на рис 67 и рис.68:

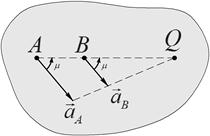
Рис. 67

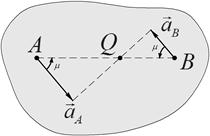
Рис.68

2. Известны угловая скорость , угловое ускорение 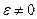, угол наклона вектораабсолютного ускорения точки к расстоянию от этой точки до МЦУпрямой, то есть 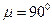, тогда: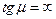

Положение МЦУ в этом случае определяется построением, приведенным на рис 69 и рис.70:

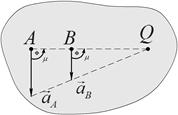
Рис. 69

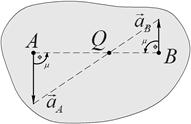
Рис.70

3. Известны ускорения двух точек А и В равные по модулю и одинаковые по направлению. Положение МЦУ в этом случае определяется построением, приведенным на рис.73. В этом случае МЦУ находится в бесконечности. Распределение ускорений будет таким же, как при поступательном движении.

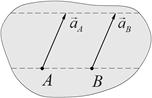
Рис.71

Пример 19 (18.34[9])

Ускорения концов однородного стержня АВ длины 12 см, совершающего плоскопараллельное движение, перпендикулярны АВ и направлены в одну сторону, причем 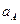= 24 см/с², 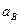= 12 см/с^2.. Определить угловую скорость и угловое ускорение стержня, положение мгновенного центра ускорений, а также ускорение его центра тяжести С.

Решение:

Находим положение мгновенного центра ускорений, который находится на продолжении отрезка АВ за точкой В (Рис.72).

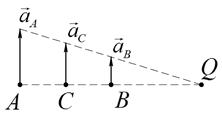
Рис.72

Составим отношение:

.

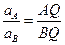Подставив значения, получим:

.

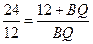Длина отрезка от точки В до МЦУ - BQ =12 см.

Длина отрезка от точки А до МЦУ - АQ =24 см.

Так как угол наклона вектораабсолютного ускорения точки к расстоянию от этой точки до МЦУпрямой, то 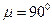, и 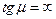. Учитывая, что 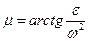, получаем .

Используя формулу: 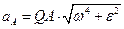, или: .

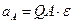Определяем угловое ускорение: 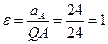с^-1.

Для определения ускорения средней точки С стержня АВ находим расстояние от точки С до МЦУ. Оно равно: АС + ВС = 6+12=18 см.

Ускорение точки С:

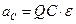
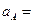18 1=18 см/с².

Примечание: применение мгновенного центра ускорений связано с трудоемкими методами нахождения его положения, поэтому определение ускорений точек плоской фигуры проще выполнять через полюс.

4. Практическое занятие по теме «Плоскопараллельное движение».

Задачей практических занятий является изучение методов расчета типовых задач, а также практическое осмысление основных теоретических положений курса. При решении задач обращается внимание на логику решения, на физическую сущность используемых величин, их размерность. Далее проводится анализ полученного решения, результат сопоставляется с реальными объектами, что вырабатывает у студентов инженерную интуицию.

Под умением применять законы и уравнения при анализе и расчете движений звеньев механизма понимаются следующие умения:

- умение определить вид движения тела;

- умение по виду движения тел и данным поставленной задачи определить закон (теорему, уравнение, принцип), с помощью которого задачу можно решить.

Перед практическим занятием необходимо разобрать материал, изложенный на лекции и выполнить самостоятельную работу, предусмотренную рабочим планом. Для этого используются: конспект лекций, соответствующие разделы печатных и электронных учебников, ответы на вопросы для самоконтроля знаний. После практического занятия самостоятельно решить рекомендованные задачи и расчетно-графические работы.

Решение любой задачи включает в себя четыре принципиально важных этапа:

- изучение (анализ) содержания задачи, краткая запись условий и требований;

- поиск способа (принципа) решения и составление плана решения;

- осуществление решения, проверка правильности и его оформление;

- обсуждение (анализ) проведенного решения, отбор информации, полезной для дальнейшей работы.

Решить учебную задачу по теоретической механике – значит найти последовательность общих положений механики (законов, формул, определений, правил), использование которых позволяет получить то, что требуется в задаче, - ее ответ.

При решении задач следует:

- определить к какому разделу теоретической механики относится рассматриваемая задача;

- усвоить теоретический материал на изучаемую тему;

- выписать предложенные на лекциях, рекомендованных учебниках и учебных пособиях алгоритмы решения задач на данную тему;

- разобрать задачи, рассмотренные на практических занятиях и имеющиеся в учебниках и пособиях примеры решения задач;

- записать краткое условие задачи;

- определиться с методом решения задачи;

- выписать математическое выражение выбранного метода;

- сделать четкий рисунок в выбранном масштабе, соответствующий условию задачи и методу решения;

- запись уравнений и их решение приводить в буквенном виде, численные значения подставлять в конечные выражения;

- привести таблицу ответов, полученных величин.

В сборниках задач по теоретической механике ([9]) приводятся задачи двух видов: на усвоение учебного материала (стандартные задачи) и активное использование изученного материала. Основная учебная функция упражнений по решению стандартных задач - перевод знаний, усвоенных на уровне воспроизведения, на уровень знаний – умений. Для таких задач имеются способы решения, одни из которых описаны в самих задачниках, другие анализируются на практических занятиях. Решение задач на активное использование изученного материала – нестандартных или проблемных, поисковых, творческих, олимпиадных задач это исследовательская работа студента первокурсника.

4.1 Цель занятия:

-знать разложение плоскопараллельного движения на поступательное и вращательное;

- уметь определять закон движения какой-либо точки и ее траекторию;

-знать способы определения мгновенного центра скоростей;

-знать определение угловой скорости тела и линейной скорости точек через МЦС;

-знать определение ускорений через полюс;

-знать способы определения мгновенного центра ускорений.

4.2 Вопросы для подготовки к практическому занятию:

1. Задание положения и движения плоской фигуры, движущейся в своей плоскости. Уравнения движения.

2. Разложение плоскопараллельного движения на составляющие.

3. Кинематические характеристики плоского движения:

3.1. Скорость точки

3.1.1. Теорема о проекциях скоростей двух точек на ось, проходящую через эти точки;

3.1.2. Мгновенный центр скоростей: определение, способы нахождения; нахождение скоростей точек плоской фигуры с помощью мгновенного центра скоростей.

3.2. Ускорение точки

3.2.1. Вычисление ускорения через полюс.

3.2.2 Мгновенный центр ускорений: определение, способы нахождения; нахождение ускорений через мгновенный центр ускорений.

4.3.1. Задачи на определение различных кинематических параметров при плоском движении с помощью формулы распределения скоростей (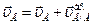) рекомендуется решать в следующем порядке:

1) анализируется движение всех звеньев механизма, и определяются те из них, которые совершают плоское движение;

2) выбираем полюс – такую точку плоской фигуры, скорость которой известна или ее можно найти по условию задачи;

3) находим вектор скорости полюса ();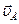

4) изображаем вектор скорости полюса 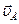, приложив его в той точке, скорость которой нужно найти по условию задачи;

5) находим скорость искомой точки, получившейся при вращении плоской фигуры вокруг полюса 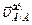, который направлен перпендикулярно звену АВ в сторону угловой скорости вращения плоской фигуры;

6) находим величину и направление скорости данной точки либо по теореме косинусов, либо спроектировав векторное равенство формулы распределения скоростей на две взаимно ортогональные оси координат.

4.3.2. Задачи на определение различных кинематических параметров при плоском движении с помощью нахождения мгновенного центра скоростей рекомендуется решать в следующем порядке (см. пример 20):

1) анализируется движение всех звеньев механизма, и определяются те из них, которые совершают плоское движение;

2) находится положение мгновенного центра скоростей (МЦС) на пересечении перпендикуляра к скоростям двух известных точек;

3) определяется мгновенная угловая скорость плоской фигуры (звена, совершающего плоское движение);

4) определяются скорости всех точек плоской фигуры как произведение угловой скорости на расстояние от точки до МЦС; (алгоритм решения задач на определение скоростей приведен в пункте 2.4.е) данного пособия).

Дата добавления: 2014-12-27