
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 16
|
|
|
|
Линейка АВ длиной 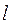 = 40 см. движется в плоскости чертежа. В некоторый момент времени ускорение точки А
= 40 см. движется в плоскости чертежа. В некоторый момент времени ускорение точки А 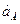 = 40 см/с2 и совпадает с направлением АВ. Определить ускорение точки В, если
= 40 см/с2 и совпадает с направлением АВ. Определить ускорение точки В, если 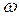 = 1 рад/с;
= 1 рад/с; 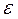 = 0,5 рад/с2.
= 0,5 рад/с2.
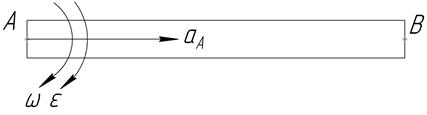
Рис.49
Решение:
Выбираем за полюс точку А, тогда: 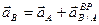 ,
,
учитывая, что 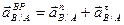 , получим
, получим 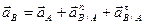 .
.
Нормальное ускорение всегда известно по модулю и направлению (направлено к полюсу, т.е. к точке А) и по модулю равно:
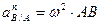 =1
=1  40=40 см/с2.
40=40 см/с2.
Касательное ускорение направлено в сторону углового ускорения, перпендикулярно нормальному ускорению и по модулю равно: 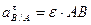 =0,5
=0,5  40=20 см/с2;
40=20 см/с2;
Введём координатные оси и покажем направления ускорений (Рис.50):
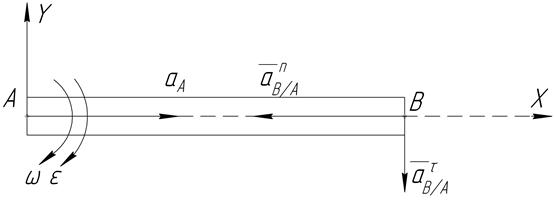
Рис.50
Спроектируем векторное равенство на координатные оси X и Y:
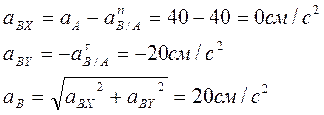
Пример 17 (18.26[9])
Груз 1, связанный посредством нерастяжимой нити с катушкой 2, опускается вертикально вниз по закону x=t2 м. При этом катушка 2 катится без скольжения по неподвижному горизонтальному рельсу. Определить скорости точек С, А, В, О и Е катушки в момент времени t = 1 c в положении, указанном на рис. 44, а также угловую скорость катушки, если AD 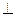 СE, СD=2OC=0,2 м.
СE, СD=2OC=0,2 м.
Рис.51
Решение:
По заданному условием задачи закону движения груза 1,определяем его скорость (см. пример 15, Рис. 44).
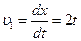 м/с
м/с
Скорость точки D, общей для нити и катушки, направлена вдоль нити и, поскольку нить считается нерастяжимой, имеет модуль, равный модулю скорости груза
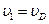
Движение катушки плоское (катушка движется в плоскости рисунка). По условию задачи катушка катится без скольжения. Установив положение мгновенного центра скоростей, который находится в точке касания катушки и неподвижного рельса (то есть, в точке О) по известной скорости точки D находим угловую скорость и угловое ускорение катушки:
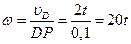 с-1
с-1
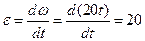 с-2
с-2
Отсюда при t = 1 c получим:
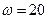 с-1
с-1
В качестве полюса выберем центр катушки С, который движется по прямолинейной траектории. Скорость центра катушки:
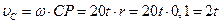 м/с
м/с
Вектор ускорения точки С направлен вдоль этой траектории (Рис.52), а его модуль определяем с помощью выражения:
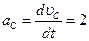 м/с2.
м/с2.
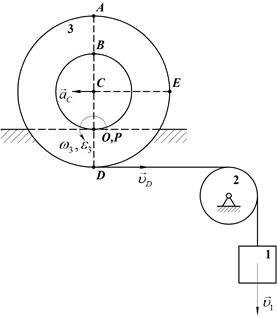
Рис.52
Ускорения точек А, В, D, О и E определим с помощью общей формулы ускорений. Для ускорения точки А запишем:
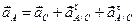 .
.
Учитывая полученные значения угловой скорости и углового ускорения катушки, находим значения нормального и касательного ускорений:
 м/с2;
м/с2; 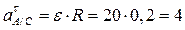 м/с2.
м/с2.
Спроектировав векторное равенство на координатные оси х и у, получим (Рис.53):
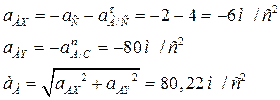
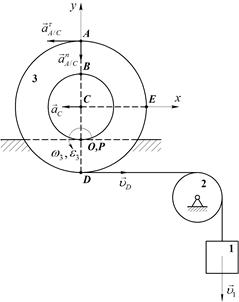
Рис.53
Повторяя описанное решение для точек В, Е, О и D будем иметь
 ,
,
где:
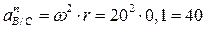 м/с2
м/с2
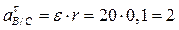 м/с2
м/с2
Проекции на координатные оси (Рис.54):
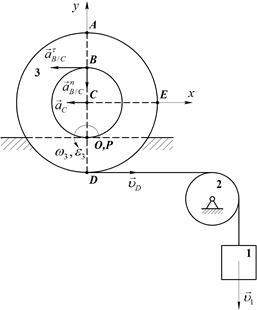
Рис.54
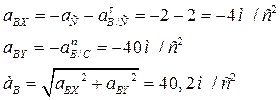
Для точки Е (Рис.55):
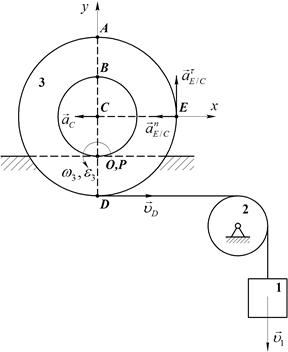
Рис.55
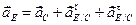
где:
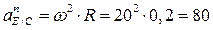 м/с2
м/с2
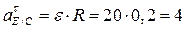 м/с2
м/с2
Проекции на оси координат:
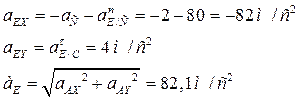
Для точки О, совпадающей с мгновенным центром скоростей катушки (Рис.56):
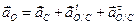 ,
,
где:
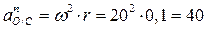 м/с2
м/с2
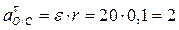 м/с2
м/с2
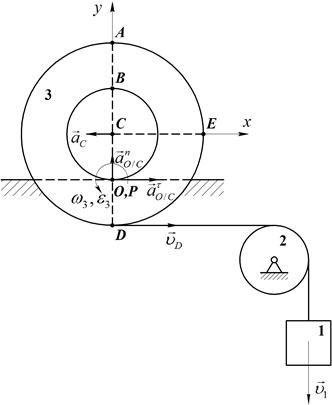
Рис.56
Проекции на оси координат:
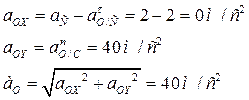
Для точки D:
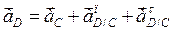
где:
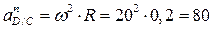 м/с2
м/с2
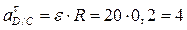 м/с2
м/с2
Проекции на оси координат (Рис.57):
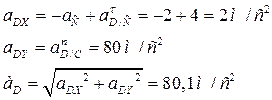
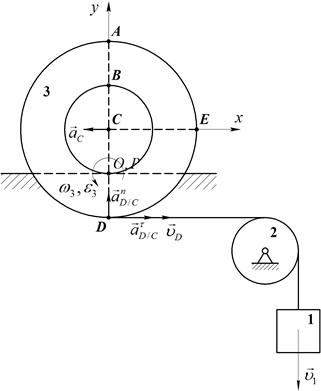
Рис.57
Пример 18 (18.34[9])
Ускорения концов однородного стержня АВ длины 12 см, совершающего плоскопараллельное движение, перпендикулярны АВ и направлены в одну сторону, причем 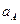 = 24 см/с2,
= 24 см/с2, 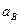 = 12 см/с2.. Определить угловую скорость и угловое ускорение стержня, а также ускорение его центра тяжести С.
= 12 см/с2.. Определить угловую скорость и угловое ускорение стержня, а также ускорение его центра тяжести С.
Решение:
Для решения задачи используем общую формулу плоского поля ускорений.
Выбираем за полюс точку А, тогда: 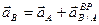 , учитывая, что,
, учитывая, что, 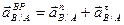
получим:
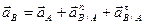 .
.
Нормальное (центростремительное) ускорение направлено к полюсу, т.е. к точке А и по модулю равно: 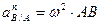 ;
;
где 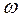 - мгновенная угловая скорость стержня.
- мгновенная угловая скорость стержня.
Касательное ускорение направлено в сторону углового ускорения E, перпендикулярно нормальному ускорению и по модулю равно: 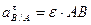 .
.
Введём координатные оси и покажем направления ускорений, (так как направление углового ускорения нам не известно, то вектор касательного ускорения 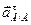 направляем перпендикулярно нормальному ускорению в любую сторону) (Рис.58):
направляем перпендикулярно нормальному ускорению в любую сторону) (Рис.58):
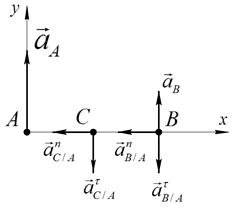
Рис.58
Спроектировав векторное уравнение на оси координат х и у, получим:
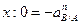 ;
;
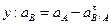 .
.
В результате:
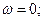
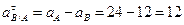 см/с2.
см/с2.
Зная касательное ускорение, определяем угловое ускорение звена АВ: 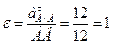 с-2.
с-2.
По известным значениям угловой скорости и углового ускорения стержня можно найти ускорение любой его точки. Записываем общую формулу плоского поля ускорений для ускорения точки С:
 ,
,
где: нормальное ускорение при вращательном движении точки С вокруг точки А 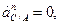 так как угловая скорость звена АВ равна нулю. Касательное ускорение при вращательном движении точки С вокруг точки А
так как угловая скорость звена АВ равна нулю. Касательное ускорение при вращательном движении точки С вокруг точки А 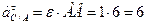 см/с2.
см/с2.
Проектируя равенство (26) на координатные оси, получим:
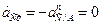 ;
;
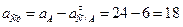 см/с2.
см/с2.
Получили ускорение точки С:
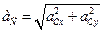
аС =18 см/с2.
Направление можно определить по направляющим косинусам.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 922; Нарушение авторских прав?; Мы поможем в написании вашей работы!