Пример 11

Кривошип ОА эпициклического механизма (Рис.35.) вращается с угловой скоростью вокруг неподвижной оси О. Колесо 1, вращается вокруг той же оси с угловой скоростью . Определить угловую скорость шестерни 2, если угловая скорость кривошипа ОА равна 2 рад./сек., угловая скорость колеса 1 равна 3 рад./сек., радиус первого колеса r₁ = OB = 20 см., радиус шестерни 2 r₂ = AB = 10 см.

Решение:

Определяем линейную скорость точек А и В, учитывая, что точка О – мгновенный центр скоростей колеса 1 и кривошипа ОА:

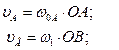
Точка В (Рис. 35)- это точка касания колес 1 и 2, а так как колеса вращаются без проскальзывания, то окружные скорости на поверхности соприкасающихся колес будут одинаковы, то есть .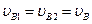

Определим положение мгновенного центра скоростей шестерни 2. В этом случае мгновенный центр скоростей находится в точке пересечения общего перпендикуляра к скоростям и прямой, соединяющей концы векторов скоростей. Подставив значения, получим:

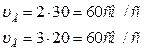
Скорости точек А и В одинаковы по модулю и по направлению - 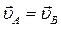, то есть в этом случае точка пересечения перпендикуляров находится в бесконечности, т.е. расстояния РА = РВ = ∞, поэтому мгновенный центр скоростей шестерни 2 - Р₂ лежит в бесконечности, и она совершает мгновенное поступательное движение.

Рис.35

5) Качение тела по неподвижной поверхности.

5.1 Качение без скольжения тела по неподвижной поверхности.

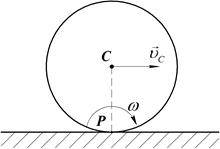
Рис. 36

Пусть колесо катится без скольжения и буксования (Рис.36). Скорость центра колеса - 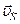. Колесо совершает плоскопараллельное движение, состоящее из поступательного движения, когда все точки движутся со скоростью полюса 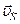, и вращательного движения вокруг полюса С. Точка контакта с неподвижной поверхностью является мгновенным центром скоростей Р. Угловая скорость колеса:

,

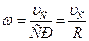то есть движение колеса можно представить как вращение в данный момент вокруг мгновенного центра скоростей Р с угловой скоростью .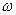

5.2 Движение со скольжением тела по неподвижной поверхности

Пусть колесо катится со скольжением. Скорость центра колеса - 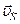. Точка контакта с неподвижной поверхностью не является в этом случае мгновенным центром скоростей. Возможны три случая.

а) Пусть скорость точки контакта О - . В данном случае векторы и 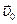параллельны и лежат на общем перпендикуляре к их скоростям, следовательно, на этом перпендикуляре находится и мгновенный центр скоростей диска. Причем, так как векторы и 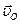направлены в одну сторону, мгновенный центр скоростей расположен с внешней стороны отрезка, соединяющего точки С и О (Рис.37).

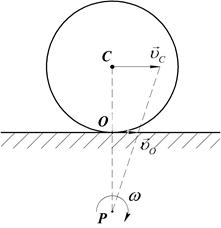
Рис.37

Угловая скорость колеса:

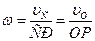
Учитывая, что СР=ОР+R, после преобразования получим:

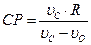, отсюда:

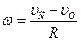
Примечание: так же происходит движение колеса при его экстренном торможении, когда оно, не вращаясь, скользит по рельсу (движение колеса «юзом», при этом происходит потеря сцепления колеса с рельсом).

б) Пусть скорость точки контакта О - 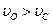, при этих условиях мгновенный центр скоростей будет расположен выше центра колеса (Рис.38).

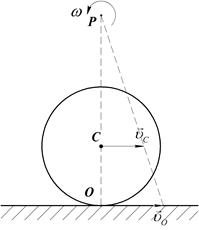
Рис.38.

Угловая скорость колеса:

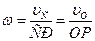
Учитывая, что ОР=СР+R, после преобразования получим:

, отсюда:

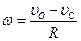
в) Пусть скорость точки контакта О - 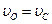, при этих условиях мгновенный центр скоростей будет находиться в бесконечности, колесо будет совершать мгновенное поступательное движение, при котором угловая скорость 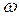равна нулю. (Рис.39).

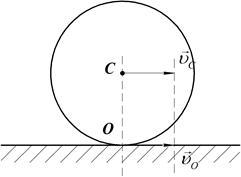
Рис.39

5.2 Движение с буксованием тела по неподвижной поверхности

Пусть колесо движется с буксованием. Скорость центра колеса - 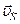. Скорость точки контакта 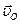направлена в противоположную сторону скорости центра 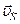. Скорости двух точек параллельны, и эти точки лежат на общем перпендикуляре к их скоростям. В этих случаях МЦС находится как точка пересечения общего перпендикуляра с прямой соединяющей концы векторов скоростей (Рис.40).

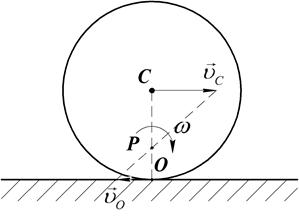
Рис.40

Угловая скорость

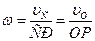
Учитывая, что ОР=R - СР, после преобразования получим:

,

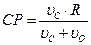отсюда:

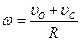
Пример.12 (16.31 [9])

Колесо радиуса R катится без скольжения по прямолинейному участку пути (рис.41); скорость его центра постоянна и равна .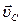

Определить скорости точек А, В, К, D, принадлежащих ободу колеса, по величине и по направлению и его угловую скорость.

Решение:

Колесо совершает плоское движение (движется в плоскости рисунка). Скорости точек найдем с помощью мгновенного центра скоростей. Мгновенный центр скоростей это такая точка на плоскости чертежа, через которую проходит мгновенная ось вращения колеса, ее скорость равна нулю и она находится в точке Р. По заданной скорости точки С, используя формулу Эйлера, определим угловую скорость колеса: .

Учтем, что точки А, В, К, D описывают окружности вокруг мгновенного центра скоростей со скоростями, векторы которых перпендикулярны отрезкам, соединяющим точку и мгновенный центр скоростей, и, модуль скорости точки равен произведению угловой скорости колеса, умноженной на длину отрезка от точки до мгновенного центра скоростей, находим:

- скорость точки А:

;

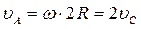- скорости точек В и D одинаковы, так как они находятся на одинаковом расстоянии от МЦС. Отрезок ВР=DP: определим по теореме Пифагора:

ВР=DP = 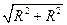= R ;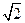

Скорость точек В и D:

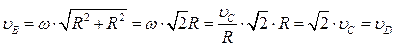
- скорость точки К:

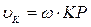; где отрезок КР определим по теореме косинусов:

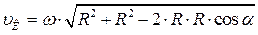
Учитывая направление скорости 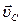, приходим к выводу, что направление скоростей точек будут такими как показано на рис.42.

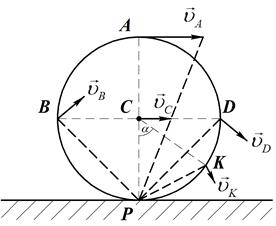
Рис. 41

Пример 13. Определить положение мгновенного центра скоростей звена АВ механизма, представленного на рис.42.

Мгновенный центр скоростей колеса 1 находится в точке Р₁, поэтому скорость точки А направлена перпендикулярно отрезку Р₁А (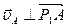). Мгновенный центр скоростей колеса 2 находится в точке Р₂, поэтому скорость точки В направлена перпендикулярно отрезку Р₂А (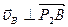). Продолжив Р₁А и Р₂В до взаимного пересечения, получим Р₃ (Рис.43) – мгновенный центр скоростей звена АВ.

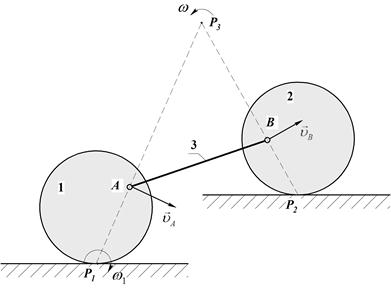
Рис.42

Дата добавления: 2014-12-27