Вычисление ускорения точек методом двукратного проектирования

Ускорение любой точки плоской фигуры геометрически складывается из ускорения поступательного движения какой-либо точки, принимаемой за полюс и ускорения этой точки во вращательном движении плоской фигуры вокруг полюса.

Вычисление ускорений через полюс.

Определение ускорений при плоскопараллельном движении

а) Определение:

Полюсом при вычислении ускорений может считаться любая точка, ускорение которой в данный момент известно (или его можно легко найти).

б) Основные формулы:

По теореме о разложении плоского движения оно является совокупностью поступательного движения вместе с полюсом и вращательного движения вокруг этого полюса, поэтому:

Ускорение вращательного движения точки при вращении плоской фигуры вокруг полюса состоит из нормального (центростремительного) ускорения и касательного (тангенциального) ускорения. Примем точку А за полюс, тогда можно записать:

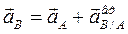, (11)

или, учитывая, что

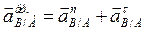
получим:

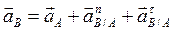; (12)

Формула (12) называется формулой Ривальса, которая вместе с формулой (1) составляет математическую основу модели плоскопараллельного движения твердого тела.

Для любой другой точки аналогично:

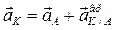
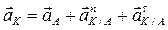(13)

где нормальное ускорение всегда известно по модулю и по направлению (направлено по звену к полюсу А). Модули нормального ускорения:

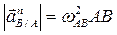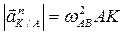; ; (14)

Если известно угловое ускорение звена по величине и направлению, то касательное ускорение точки направлено перпендикулярно нормальному ускорению в сторону углового ускорения .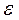

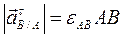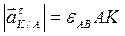; . (15)

Так как угловая скорость 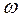и угловое ускорение 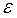звена известны, то для точки С аналогично:

,

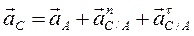где:

;

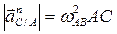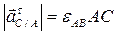
Модуль и направление ускорения точек В, К и С можно найти геометрически построением соответствующего параллелограмма.

Проиллюстрируем полученные равенства (Рис.46):

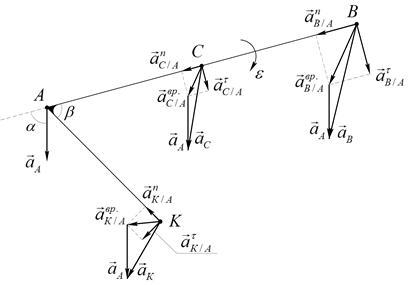
Рис. 46

Ускорение любой точки можно определить аналитически почленным проектированием уравнений (12), (13) на две взаимно перпендикулярные оси координат. Удобно одну ось направлять по звену (так как нормальное ускорение направлено по звену к полюсу), другую перпендикулярно звену (по линии действия касательного ускорения).

Пусть известно линейное ускорение полюса по величине и по направлению. Будем считать, что известна угловая скорость тела или звена , угловое ускорение тела или звена 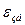(то есть известны нормальные и касательные ускорения по величине и по направлению). Ускорение искомой точки, не известно ни по величине, ни по направлению, тогда, спроектировав (12), на оси координат «x» и «y» получим (Рис.47):

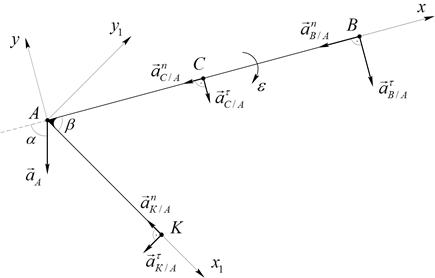
Рис.47

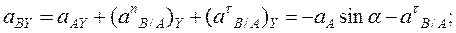
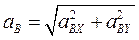
Направление вектора ускорения найдем по направляющим косинусам:

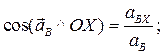
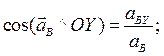
Для определения ускорения точки К, введем новые координатные оси X₁ и Y₁ (Рис.47). Спроектировав уравнение (13) на эти оси координат получим:

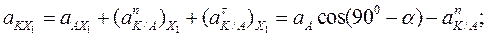
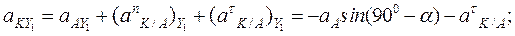
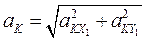
Направление вектора ускорения найдем по направляющим косинусам:

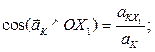
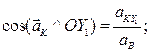
Для любой другой точки, (например, С) аналогично (Рис.47):

Спроектировав уравнение (16) почленно на две взаимно перпендикулярные оси координат, получим:

;

;

.

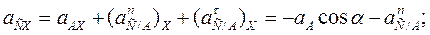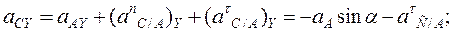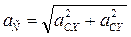Дата добавления: 2014-12-27