
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 14
|
|
|
|
Вал 1 вращается вокруг неподвижной оси О с угловой скоростью  и опирается при помощи роликов на обойму подшипника. Радиус вала 1 равен R, радиус ролика равен r. Определить скорость центра ролика, его угловую скорость и направление вращения.
и опирается при помощи роликов на обойму подшипника. Радиус вала 1 равен R, радиус ролика равен r. Определить скорость центра ролика, его угловую скорость и направление вращения.
Решение:
Обозначим точку соприкосновения вала с роликом через А, модуль её скорости: 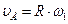 . Точка касания ролика с неподвижной обоймой есть мгновенный центр скоростей (Р) ролика. Угловая скорость ролика:
. Точка касания ролика с неподвижной обоймой есть мгновенный центр скоростей (Р) ролика. Угловая скорость ролика: 
Модуль скорости центра С ролика:  ;
;
Ролик вращается вокруг своего центра против хода часовой стрелки и бегает вокруг вала по ходу часовой стрелки (Рис.43.).
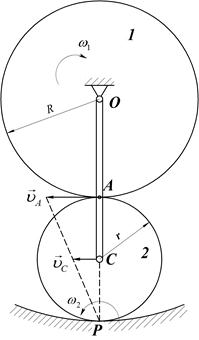
Рис.43
Пример 15 (16.34[9])
Груз 1, связанный посредством нерастяжимой нити с катушкой 2, опускается вертикально вниз по закону x=t2 м. При этом катушка 2 катится без скольжения по неподвижному горизонтальному рельсу (Рис.44). Определить скорости точек С, А, В, О и Е катушки в момент времени t = 1 c в положении, указанном на рис. 45, а также угловую скорость катушки, если AD 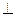 СE, СD=2OC=0,2 м.
СE, СD=2OC=0,2 м.
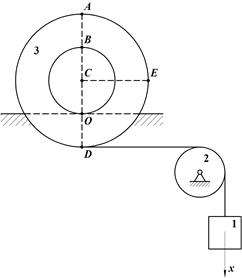
Рис.44
Решение
По заданному закону движения груза 1 определяем его скорость
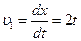 м/с
м/с
При t = 1 c, получим: 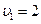 м/с
м/с
Скорость точки D, общей для нити и катушки, направлена вдоль нити и, поскольку нить считается нерастяжимой, имеет модуль, равный модулю скорости груза: 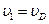
Движение катушки плоское (катушка движется в плоскости рисунка). Скорости точек С, А, В, О, и Е катушки определим с помощью ее мгновенного центра скоростей, который находится в точке касания катушки и неподвижного рельса (то есть в точке О), так как по условию задачи катушка катится без скольжения, а значит 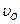 =0. Установив положение мгновенного центра скоростей, по известной скорости точки D находим угловую скорость катушки:
=0. Установив положение мгновенного центра скоростей, по известной скорости точки D находим угловую скорость катушки:
 с-1
с-1
Учитывая, что точки А, В, С, и Е описывают окружности вокруг мгновенного центра скоростей Р со скоростями, векторы которых 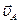 ,
, 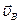 ,
,  , и
, и 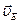 перпендикулярны радиусам этих окружностей АР, ВР, С Р и ЕР определяем линейные скорости точек (Рис.45):
перпендикулярны радиусам этих окружностей АР, ВР, С Р и ЕР определяем линейные скорости точек (Рис.45):
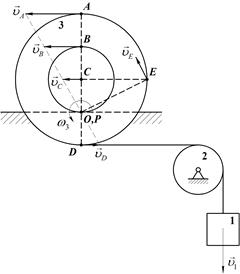
Рис.45
 м/с;
м/с;
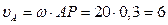 м/с;
м/с;
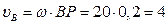 м/с;
м/с;
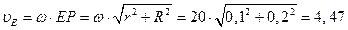 м/с;
м/с;
е). Алгоритм решения задач на тему: «Скорости точек плоской фигуры. Мгновенный центр скоростей».
1. Если дан плоский механизм, состоящий из нескольких звеньев, то при решении задачи рассматривают последовательно движение отдельных звеньев механизма, начиная от того звена, движение которого задано.
2. При переходе от одного звена к другому определяют скорости тех точек, которые являются общими для этих двух звеньев механизма.
3. Следует подчеркнуть, что мгновенный центр скоростей можно находить только для каждого звена в отдельности, то же относится и к угловым скоростям.
4. Рекомендуется: МЦС и угловые скорости звеньев обозначать Р1,Р2,Р3,… 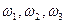 ,…, где индексы 1,2,3 соответствуют номеру звена.
,…, где индексы 1,2,3 соответствуют номеру звена.
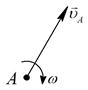
Таблица 1. Различные способы определения положения МЦС
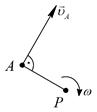
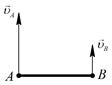
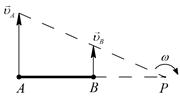
| Дано | Исходная схема | Построение МЦС | Можно определить |
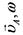
| 
| 
| 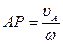 ; ;

|
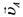 и и 
| 
| 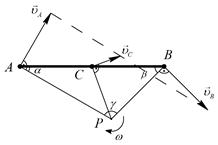
| 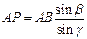 ; ;
 ; ;
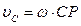
|
| 
| 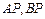 ; ;
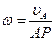 ; ;
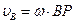
| |
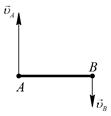
| 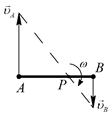
| 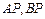 ; ;
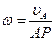 ; ;
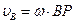
| |
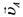 и линия действия и линия действия 
| 
| 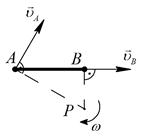
|  ; ;
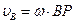
|
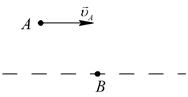
| 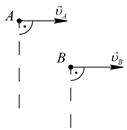
| 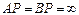 ; ;
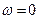 ; ;
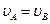
| |
| Качение без скольжения | 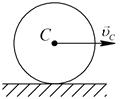
| 
| 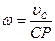 ; ;
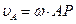
|
и). Упражнения и консультации
Примечание:
Консультацией пользуйтесь в том случае, когда затрудняетесь ответить на вопросы или хотите проверить правильность своего ответа.
Задание Консультация
Зная угловую скорость звена О1А и размеры звеньев кривошипно-коромыслового механизма, определить линейную скорость точек А, Д, С, В, угловые скорости звеньев АС и О2В и положение МЦС звена АС механизма в указанном положении.
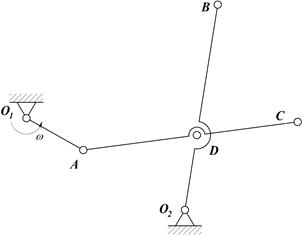
| |
1. 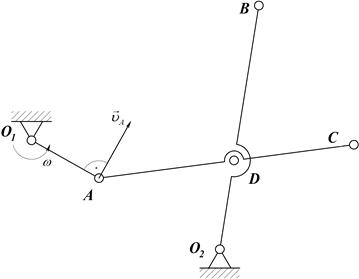
| 1. Последовательно рассмотрим движение каждого звена. Кривошип ОА вращается вокруг неподвижной оси О1 с известной угловой скоростью 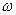 . Мгновенный центр скоростей звена О1А находится в точке О1 так как это стойка. Точка А движется по окружности радиуса О1А со скоростью . Мгновенный центр скоростей звена О1А находится в точке О1 так как это стойка. Точка А движется по окружности радиуса О1А со скоростью 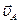 , вектор которой перпендикулярен звену О1А. Модуль вектора , вектор которой перпендикулярен звену О1А. Модуль вектора 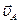 определяется по формуле Эйлера, учитывая, что точка О1 - мгновенный центр скоростей кривошипа О1А получим: определяется по формуле Эйлера, учитывая, что точка О1 - мгновенный центр скоростей кривошипа О1А получим: 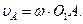
|
2. 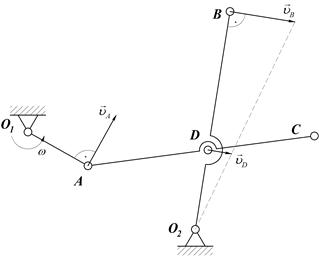
| 2. Коромысло О2В вращается вокруг неподвижной оси О2. Точка В движется по окружности радиуса О2В со скоростью 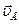 , вектор которой перпендикулярен звену О2В. Точка Д движется по окружности радиуса О2Д со скоростью , вектор которой перпендикулярен звену О2В. Точка Д движется по окружности радиуса О2Д со скоростью 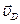 , вектор которой перпендикулярен звену О2В. Показываем на схеме линии действия скоростей , вектор которой перпендикулярен звену О2В. Показываем на схеме линии действия скоростей 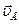 и и 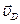 направляя их перпендикулярно коромыслу в любую сторону, так как направление угловой скорости звена О2В нам не известно. направляя их перпендикулярно коромыслу в любую сторону, так как направление угловой скорости звена О2В нам не известно.
|
3. 
| 3.Определяем положение МЦС звена АС. Мгновенный центр скоростей звена АС находится в точке пересечения перпендикуляров, восстановленных из точек А и D кскоростям 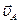 и и 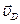 . Из чертежа видно, что МЦС совпадает с точкой О2 Определяем угловую скорость звена АС. . Из чертежа видно, что МЦС совпадает с точкой О2 Определяем угловую скорость звена АС. 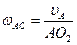 . Отрезок АО2 можно определить по теореме косинусов. Линейные скорости точек D и В определяем по формуле Эйлера: . Отрезок АО2 можно определить по теореме косинусов. Линейные скорости точек D и В определяем по формуле Эйлера: 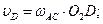 
|
4. 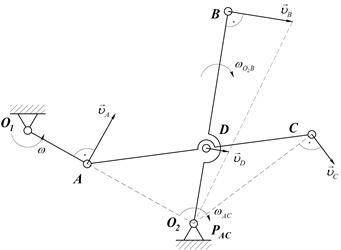
| 4.Для определения линейной скорости точки С, которая принадлежит звену АС, соединяем точку С с мгновенным центром скоростей звена АС – точкой О2. Скорость очки С будет направлена перпендикулярно отрезку, О2С в сторону угловой скорости  . Модуль скорости точки С: . Модуль скорости точки С: 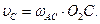 Отрезок О2С можно определить по теореме косинусов. Отрезок О2С можно определить по теореме косинусов.
|
Задание Консультация
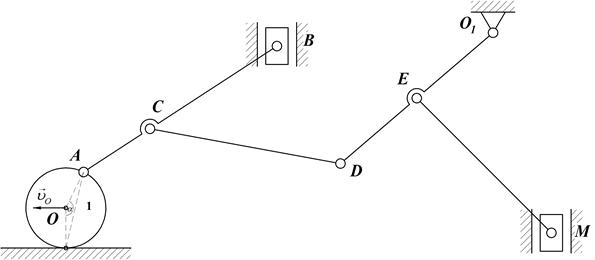
Зная линейную скорость центра колеса 1 - 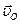 по модулю и направлению (колесо катится по неподвижной плоскости без проскальзывания) и размеры звеньев многозвенного механизма, определить линейную скорость точек: А, В, С, D, Е, М, угловые скорости звеньев АВ, О1D, СD, ЕМ и положение МЦС звеньев механизма в указанном положении. по модулю и направлению (колесо катится по неподвижной плоскости без проскальзывания) и размеры звеньев многозвенного механизма, определить линейную скорость точек: А, В, С, D, Е, М, угловые скорости звеньев АВ, О1D, СD, ЕМ и положение МЦС звеньев механизма в указанном положении.
| |
1.
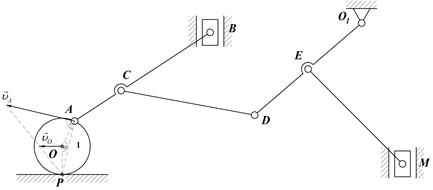
| 1.Определяем положение МЦС колеса – точка соприкосновения с неподвижной плоскостью Р Определяем угловую скорость колеса 1: 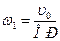 . Определяем линейную скорость точки А: . Определяем линейную скорость точки А: 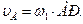 Скорость Скорость 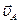 направлена перпендикулярно отрезку, который соединяет точку А и направлена перпендикулярно отрезку, который соединяет точку А и  в сторону. угловой скорости колеса в сторону. угловой скорости колеса 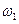 . Длину отрезка АР определяем по теореме косинусов. . Длину отрезка АР определяем по теореме косинусов.
|
2.

| 2. Ползун В совершает поступательное движение по вертикальным направляющим. Скорость ползуна В известна по линии действия. Направляем скорость 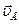 по вертикали. Определяем положение МЦС звена АВ – РАВ, который находится на пересечении перпендикуляров восстановленных в точках А и В к скоростям по вертикали. Определяем положение МЦС звена АВ – РАВ, который находится на пересечении перпендикуляров восстановленных в точках А и В к скоростям 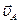 и и 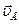 . Определяем угловую скорость звена АВ: . Определяем угловую скорость звена АВ:  . Ее направление определяется направлением линейной скорости точки А (по часовой стрелке). Определяем линейную скорость точки В по модулю: . Ее направление определяется направлением линейной скорости точки А (по часовой стрелке). Определяем линейную скорость точки В по модулю: 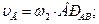 и проверяем направление скорости и проверяем направление скорости 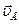 (перпендикулярно отрезку ВРАВ в сторону угловой скорости звена (перпендикулярно отрезку ВРАВ в сторону угловой скорости звена 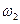 ). Точка С принадлежит звену АВ, поэтому ее скорость можно определить ). Точка С принадлежит звену АВ, поэтому ее скорость можно определить 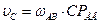 . .
|
3.
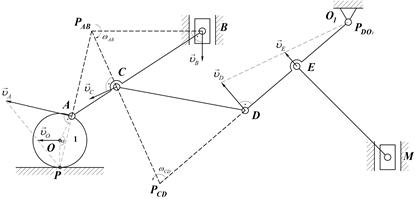
| 3.Для определения угловой скорости звена СD определим положение мгновенного центра скоростей этого звена - 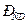 . Точка D находится на звене DO1 и для него МЦС находится в точке О1. Скорость точки D направлена перпендикулярно звену DO1. Восстанавливаем перпендикуляры в точках C и D к скоростям . Точка D находится на звене DO1 и для него МЦС находится в точке О1. Скорость точки D направлена перпендикулярно звену DO1. Восстанавливаем перпендикуляры в точках C и D к скоростям  и и 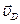 на пересечении получаем МЦС звена CD точку на пересечении получаем МЦС звена CD точку 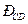 . Определяем угловую скорость звена CD по модулю: . Определяем угловую скорость звена CD по модулю: 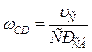 и по направлению – против часовой стрелки. Определяем скорость точки D по модулю: и по направлению – против часовой стрелки. Определяем скорость точки D по модулю: 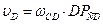 и проверяем направление – в сторону угловой скорости вращения звена CD - и проверяем направление – в сторону угловой скорости вращения звена CD -  . Определяем угловую скорость звена DO1: . Определяем угловую скорость звена DO1: 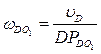 . Угловая скорость звена направлена по часовой стрелке. Скорость точки Е можно определить так как положение МЦС звена DO1 известно: . Угловая скорость звена направлена по часовой стрелке. Скорость точки Е можно определить так как положение МЦС звена DO1 известно: 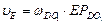
|

| 4.Ползун М совершает поступательное движение по вертикали, то есть его скорость по линии действия известна. Для определения МЦС звена ЕМ восстанавливаем перпендикуляры к скоростям 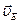 и и 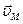 двух известных точек Е и М. На пересечении получаем точку двух известных точек Е и М. На пересечении получаем точку  -МЦС звена ЕМ. Определяем угловую скорость звена ЕМ: -МЦС звена ЕМ. Определяем угловую скорость звена ЕМ: 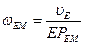 . Угловая скорость звена направлена против часовой стрелки. Определяем скорость точки М по модулю и по направлению: . Угловая скорость звена направлена против часовой стрелки. Определяем скорость точки М по модулю и по направлению: 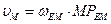 . Схема будет иметь вид, представленный на чертеже в пункте 4 таблицы. . Схема будет иметь вид, представленный на чертеже в пункте 4 таблицы.
|
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 1195; Нарушение авторских прав?; Мы поможем в написании вашей работы!