Пример 7

Определить положение МЦС кривошипно-ползунного механизма.

Решение:

Рассмотрим последовательно движение каждого звена механизма, начиная с кривошипа О₁А.

Звено О₁А совершает вращательное движение относительно точки О₁ с заданной угловой скоростью , поэтому вектор скорости точки А перпендикулярен звену О₁А (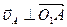). вектор скорости точки В направлен по горизонтали, так как ползун совершает поступательное движение по горизонтальным направляющим. Движение шатуна АВ является плоским (шатун движется в плоскости чертежа). Для того чтобы определить положение МЦС звена АВ необходимо знать направление скоростей двух его точек. МЦС находим как точку пересечения перпендикуляров, проведенных к векторам скоростей точек А и В, то есть восстанавливая из точки А перпендикуляр к скорости 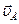и из точки В перпендикуляр к скорости 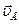получим мгновенный центр скоростей Р_АВ шатуна АВ (Рис.26).

Рис.26

2) Определение МЦС в случае, если скорости двух точек параллельны (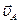 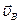), направлены в разные стороны и эти точки лежат на общем перпендикуляре к их скоростям (Рис.27).

В этом случае МЦС находится как точка пересечения общего перпендикуляра (отрезка АВ) с прямой, соединяющей концы векторов скоростей.

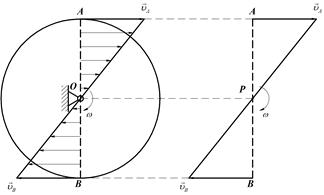
Рис. 27

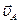
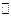
3) Определение МЦС в случае, если скорости двух точек параллельны ( 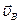), направлены в одну сторону и эти точки лежат на общем перпендикуляре к их скоростям (Рис.28).

В этом случае МЦС находится как точка пересечения общего перпендикуляра (отрезка АВ) с прямой, соединяющей концы векторов скоростей.

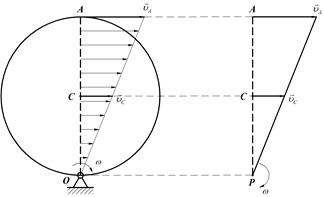
Рис. 28

Пример 8 (16,32 [9])

На рис.29 изображен суммирующий механизм, в котором две параллельные рейки движутся в одну сторону с постоянными скоростям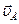и .и 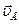. Между рейками зажат диск 2 радиуса R, катящийся по рейкам без скольжения. Определить скорость центра диска и его угловую скорость 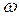. Показать, что скорость центра диска равна полусумме скоростей реек.

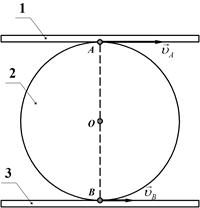
Рис. 29

Решение

Диск суммирующего механизма совершает плоское движение (движется в плоскости чертежа). Рейки механизма движутся поступательно и имеют общие точки с диском - точки А и В касания реек с диском. Поэтому заданные условием задачи скорост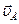и и 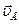равны скоростям точек А и В принадлежащим диску.

Для определения угловой скорости диска и линейной скорости его центра О построим мгновенный центр скоростей диска.

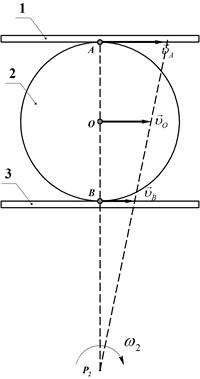
Рис. 30

В данном случае векторы 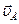, 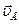и 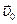параллельны и лежат на общем перпендикуляре к их скоростям, следовательно, на этом перпендикуляре находится и мгновенный центр скоростей диска. Причем, так как векторы 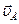и 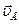направлены в одну сторону, мгновенный центр скоростей расположен с внешней стороны отрезка, соединяющего точки А и В (Рис.30).

Угловая скорость диска:

.

Из чертежа (Рис.30) видно, что АР=ВР+2R, тогда:

.

Преобразовав, получим:

;

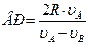то есть угловая скорость диска:

.

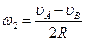Скорость центра диска О:

где ОР – расстояние от центра диска до мгновенного центра скоростей:

;

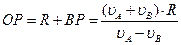Тогда:

то есть скорость центра диска равна полусумме скоростей реек.

Дата добавления: 2014-12-27