Пример 1. Муфта А (Рис.12.) скользит по вертикальным направляющим со скоростью =2 см/с

Муфта А (Рис.12.) скользит по вертикальным направляющим со скоростью 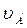=2 см/с. Стержень АВ длиной 2 см вращается вокруг точки А с угловой скоростью =2 с^-1. Найти скорость точки В в тот момент времени, когда угол 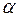= 30⁰.

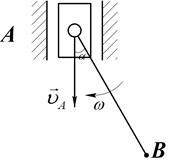
Рис. 12

Решение:

Примем точку А за полюс. Используем векторное равенство (1): .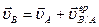

Модуль скорости при вращательном движении точки В вокруг полюса А определим по формуле:

.

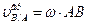Подставив значения, получим:

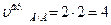см/с

Вектор скорости точки В при вращательном движении вокруг точки А перпендикулярен звену АВ (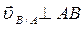) и направлен в сторону угловой скорости (Рис.13.). Модуль скорости точки В определим двумя способами:

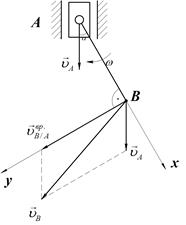
Рис. 13

1) по теореме косинусов

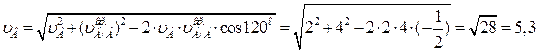см/с

2) методом проекций (ось Х направим по звену АВ, ось Y перпендикулярно звену АВ, то есть по );

Проектируем равенство (6) на оси Х и Y:

2.2 Следствие 1 - Теорема о проекциях

Формулировка: проекции скоростей двух точек плоской фигуры при плоскопараллельном движении на прямую, соединяющую эти точки равны по величине и одинаковы по направлению.

Рис. 14

Доказательство:

Пусть точка А – полюс, тогда по теореме о разложении плоского движения и в соответствии с векторным равенством (1) можно записать:

Введем координатную ось Х, совместив ее с прямой АВ. Спроектируем почленно уравнение (1) на ось Х (то естьна прямую АВ). Получим:

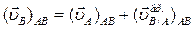
Учитывая, что вектор и проекция на прямую АВ равна нулю получим:

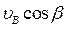= ; (5)

Теорема о проекциях– это один из самых простых способов вычисления скоростей при плоском движении.

Чтобы вычислить скорость по теореме о проекциях, необходимо знать скорость одной из точек, а также направление этих скоростей.

Пример 2 (16.11 [9])

Стержень АВ длины 0,5 м движется в плоскости чертежа (Рис.15). Скорость 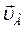( 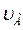= 2 м/с) образует угол 45⁰ с осью, совмещенной со стержнем АВ. Скорость 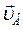точки В образует угол 60⁰ со стержнем АВ. Найти модуль скорости точки В и угловую скорость стержня .

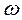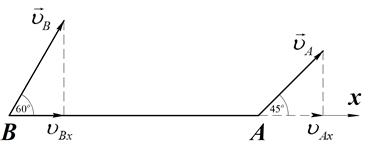
Рис.15

Решение:

Для определения модуля скорости точки В используем теорему о проекциях, согласно которой: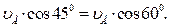

Отсюда:

м/с.

Чтобы найти угловую скорость стержня 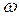, примем точку А за полюс и запишем в соответствии с (1) векторное равенство:

Спроектируем это векторное равенство на ось, перпендикулярную стержню АВ, получим:

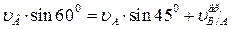
Рис.16

Отсюда:

,

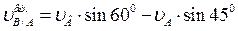где: - скорость точки В при вращательном движении вокруг полюса А, направленная перпендикулярно звену АВ в сторону угловой скорости звена .

Подставив значения, получим:

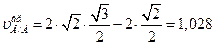м/с

Отсюда:

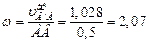с^-1

Дата добавления: 2014-12-27