Пример 6

Для тела, движущегося плоскопараллельно, в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в данный момент равна нулю. Эта точка называется мгновенным центром скоростей (МЦС).

Вычисление скоростей через мгновенный центр скоростей (МЦС)

а) Определение:

Обозначается МЦС - P. . Очевидно, что эта точка единственная, так как при наличии второй точки с нулевой скоростью фигура в данный момент была бы неподвижна и скорости всех ее точек равнялись бы нулю. Использование МЦС упрощает процедуру определения скоростей точек плоской фигуры.

б) Определение линейных скоростей точек через МЦС

Если положение МЦС найдено, то скорость любой точки плоской фигуры может быть определена посредством выбора полюса в МЦС. Для произвольной точки, например, А можно записать:

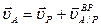; (6)

Так как 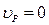, то можно записывать это равенство без векторов, то есть в этом случае векторное выражение теоремы о сложении скоростей вырождается в известную зависимость от расстояния до центра вращения:

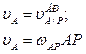(7)

Для произвольной точки В получим:

;

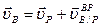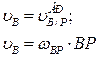; (8)

Учитывая, что для одного и того же тела (или звена), угловая скорость 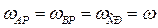, получим:

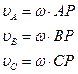(9)

Поле скоростей точек плоской фигуры в этом случае представляет собой поле вращательных скоростей относительно мгновенного центра скоростей. (Рис.19)

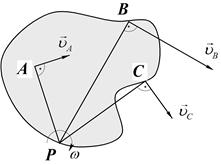
Рис.19

в). Общий метод вычисления скоростей через мгновенный центр скоростей

Чтобы определить положение мгновенного центра скоростей (Р), необходимо знать направление скоростей двух точек, например, А и В и модуль скорости одной из точек.

Пусть известна скорость точки А по модулю и по направлению, и известна скорость точки В по направлению. Известно, что эти скорости не параллельны друг другу. Восстанавливаем в точке А перпендикуляр к скорости точки А и в точке В перпендикуляр к направлению скорости точки В.

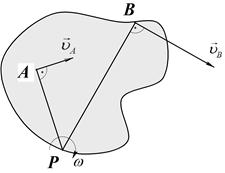
Рис.20

Мгновенный центр скоростей (Р) находится в точке пересечения перпендикуляров к скоростям, восстановленных в точках А и В (Рис.20). Направление скоростей: и .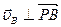

Правило:

Чтобы вычислить линейную скорость какой-либо точки тела через мгновенный центр скоростей, необходимо, угловую скорость тела умножить на длину отрезка, соединяющего точку с мгновенным центом скоростей. Скорость точки направлена перпендикулярно этому отрезку в сторону угловой скорости вращения тела (Рис.20).

Модули скоростей точек пропорциональны их расстояниям до МЦС, а это значит, чем дальше от МЦС точка, тем больше у неё скорость. Отсюда следует, что при вычислении скоростей, тело при плоском движении не совершает никакого другого движения, кроме как вращательного движения вокруг МЦС.

МЦС применяется только при вычислении скоростей и не применяется при вычислении ускорений, так как ускорение мгновенного центра скоростей не равно нулю.

г) Вычисление угловой скорости через мгновенный центр скоростей

Как следует из формул (9) пункта «б» угловую скорость вращения плоской фигуры 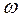, легко найти, зная линейную скорость какой-либо точки и длину отрезка от точки до мгновенного центра скоростей. Отношение линейной скорости точки тела к ее расстоянию до мгновенного центра скоростей есть величина постоянная для всех точек тела, равная его угловой скорости, то есть:

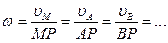(10)

Правило:

Для того чтобы определить угловую скорость тела (или звена) необходимо линейную скорость какой-либо точки тела разделить на длину отрезка, соединяющего эту точку с мгновенным центром скоростей. Направление угловой скорости (направление дуговой стрелки угловой скорости) определяется направлением вектора линейной скорости этой точки по отношению к МЦС (Рис.21).

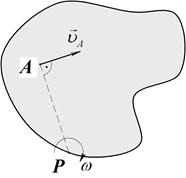
Рис.21

Пример 5 (16.11 [9])

Стержень АВ длины 0,5 м движется в плоскости чертежа (Рис.22.). Скорость 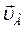( 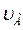= 2 м/с) образует угол 45⁰ с осью, совмещенной со стержнем АВ. Скорость 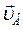точки В образует угол 60⁰ со стержнем АВ. Найти модуль скорости точки В и угловую скорость стержня .

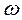Рис.22

Решение:

Для определения скорости точки В - 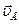и угловой скорости стержня 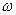, построим мгновенный центр скоростей стержня АВ. Для этого из точек А и В восстанавливаем перпендикуляры к векторам скоросте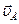й и 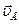до их пересечения в точке Р, являющейся мгновенным центром скоростей звена АВ (Рис.23).

Учитывая, что 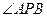=180⁰ – (30⁰+135⁰)=15⁰, определяем по теореме синусов расстояние от точки А до мгновенного центра скоростей Р:

;

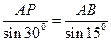Отсюда: 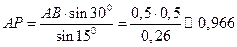м.

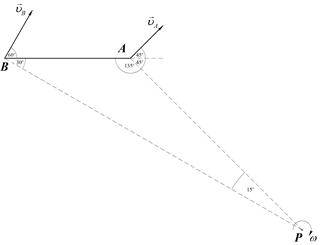
Рис.23

По известным значениям скорости точки А и отрезка АР подсчитываем значение угловой скорости стержня :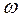

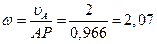с^-1.

Для определения скорости точки В определим по теореме косинусов отрезок ВР, соединяющий точку В и мгновенный центр скоростей звена АВ – точку Р:

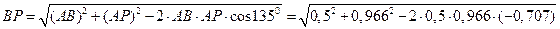
=1,366 м.

Модуль скорости точки В:

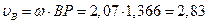м/с

Полученные результаты совпадают со значениями, полученными в примере 2.

д) Частные случаи нахождения мгновенного центра скоростей

1) Общий метод.

Чтобы определить положение мгновенного центра скоростей, необходимо знать направления скоростей двух точек.

Пусть известны скорости двух точек плоской фигуры, не параллельные друг другу (Рис.24). Мгновенный центр скоростей лежит на пересечении перпендикуляров восстановленных из точек А и В к направлениям векторов их скоростей. При этом может быть определена угловая скорость тела или звена:

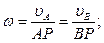
Примечание: для нахождения только положения МЦС достаточно знать лишь направления скоростей двух точек.

Рис. 24

Определить положение мгновенного центра скоростей звена АВ кривошипно-коромыслового механизма (Рис.25).

Решение:

Рассмотрим последовательно движение каждого звена механизма, начиная от кривошипа О₁А. Звено О₁А совершает вращательное движение относительно оси О₁ с заданной угловой скоростью 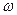. (Так как точка О₁ неподвижна, то она является мгновенным центром скоростей звена О₁А). Точка А кривошипа движется по окружности радиуса О₁А со скоростью 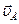, поэтому вектор скорости точки А перпендикулярен звену О₁А (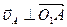). Звено О₂В совершает вращательное движение относительно оси О₂, (так как точка О₂ неподвижна, то она является мгновенным центром скоростей звена О₂В), поэтому вектор скорости точки В (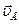) перпендикулярен звену О₂В (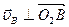). Движение шатуна АВ является плоским (шатун движется в плоскости чертежа). Для того чтобы определить положение МЦС звена АВ необходимо знать направление скоростей двух его точек. МЦС находим как точку пересечения перпендикуляров, проведенных к векторам скоростей точек А и В, то есть продолжаем О₁А и О₂В до взаимного пересечения, получим Р_АВ – мгновенный центр скоростей звена АВ (Рис.25).

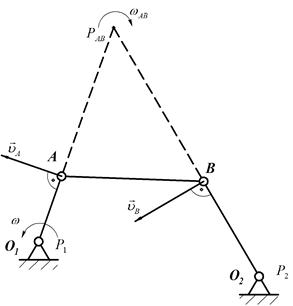
Рис.25

Дата добавления: 2014-12-27