Задачи второго типа

Задачи первого типа.

Известны (или могут быть найдены по условиям задачи) ускорение какой-нибудь точки, например, А и мгновенная угловая скорость 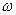тела в любой момент времени, Требуется определить мгновенное угловое ускорение E и ускорение любой другой точки В плоской фигуры.

К задачам такого типа относятся задачи качения без скольжения одного тела по неподвижной поверхности другого.

Поскольку известна зависимость угловой скорости 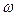от времени t, то угловое ускорение E находят путем дифференцирования 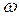. Величины неизвестных составляющих искомого вектора находят согласно уравнениям (12). Величину удобнее всего находить путем проектирования на две взаимно перпендикулярные оси.

В некоторый момент времени известна величина и направление ускорения какой-либо точки А (полюса) плоской фигуры, (или ее можно легко найти), мгновенная угловая скорость 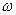и прямая, вдоль которой направлено ускорение другой точки, (например, точки В). Необходимо определить угловое ускорение фигуры и ускорение точки В, (а затем и любой другой точки фигуры) в рассматриваемый момент времени. (см. пример 16 и 21).

Пример 21

Тема: Определение скоростей и ускорений твердого тела при плоском движении.

Кривошип ОА кривошипно-ползунного механизма вращаясь вокруг неподвижной оси О с угловой скоростью ω _ОА и угловым ускорением ε _ОА, приводит в движение шатун АВ, соединенный с ним шарнирно в точке А. Ползун В перемещается в направляющих по горизонтали.

Определить скорости и ускорения точек А, В и С, для данного положения механизма, а также угловую скорость и ускорение шатуна АВ (Рис.77).

Дано:

ОА = 25 см; АВ = 50 см; АС = СВ; α = 45 ^о; ω _ОА = 2 с^-1; ε _ОА = 1 с^-2.

Найти: υ _А, а _А, υ _В, а _В, υ _С, а _С, ω _АВ, ε _АВ.

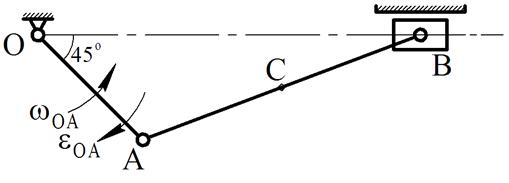
Рис. 75

Решение

1. Механизм состоит из трех подвижных звеньев: кривошипа ОА, шатуна АВ и ползуна В. Кривошип вращается вокруг неподвижной оси с заданной угловой скоростью ω _ОА. Точка А во время движения будет описывать окружность радиус которой ОА с центром в точке О. Скорость точки А - 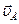направлена по касательной к этой окружности, то есть перпендикулярно звену ОА в соответствии с заданным направлением вращения угловой скорости ω _ОА кривошипа ОА. Модуль скорости точки А определяется по формуле Эйлера:

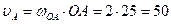см/с.

Вектор скорости ползуна В направлен вдоль горизонтали, так как ползун совершает поступательное движение по горизонтальным направляющим (Рис.77).

Для дальнейших расчетов определим углы, образованные кривошипом и шатуном (угол ), а также угол между шатуном АВ и линией движения ползуна В (угол B).

По теореме синусов:

;

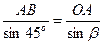Отсюда:

; ; .

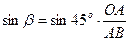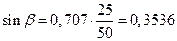Угол .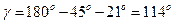

Определим длину отрезка ОВ:

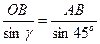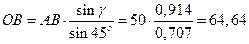; см.

2. Движение шатуна АВ плоское. Для определения угловой скорости шатуна 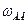построим мгновенный центр скоростей звена АВ. Как известно, для построения мгновенного центра скоростей плоской фигуры достаточно знать линии действия векторов двух ее точек. В данном случае известны скорость точки А по модулю и направлению и направление скорости точки В.

Восстанавливая перпендикуляры к скоростям 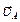из точки А и 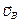из точки В, на их пересечении получаем точку Р_АВ - МЦС звена АВ (Рис.76).

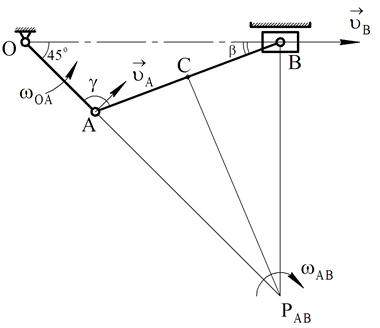
Рис. 76

Определяем расстояние от точек А и В до МЦС. Отрезок ОР_АВ:

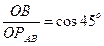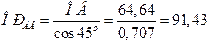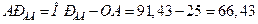; см.

см.

Определим длину отрезка ВР_АВ: 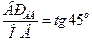, т.е. ВР_АВ = ОВ = 64,64 см.

Определим угловую скорость звена АВ:

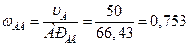с^-1.

Определим скорость точки В:

;

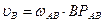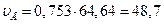см/с.

Проверяем полученный результат по теореме о проекциях. Для этого спроектируем скорость точек А и В на шатун АВ, соединяющий эти точки. Получим:

.

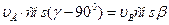Отсюда:

.

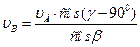Подставив значения, получим:

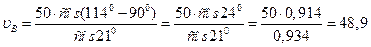см/с.

Разницу в 0,2 см/с можно объяснить погрешностью округления величин.

Скорость точки С, которая является средней точкой шатуна АВ:

;

Расстояние от точки с до МЦС - СР_АВ найдем по теореме косинусов:

;

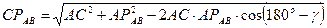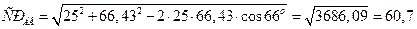см.

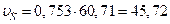см/с.

3. Определяем ускорения точек и угловое ускорение звена АВ:

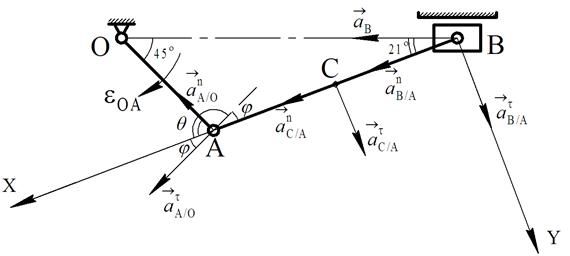
Рис.77

Определяем ускорения через полюс. Для звена ОА полюсом является точка О, так как точка О – неподвижное звено (стойка) то ее ускорение равно нулю. Точка А вращается вместе с кривошипом ОА вокруг точки О. Поэтому для точки А можно записать векторное уравнение:

;

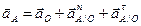где: а_о= 0; нормальное (центростремительное)ускорение точки А при вращении вокруг полюса О:

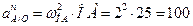см/с²;

касательное ускорение точки А при вращении вокруг полюса О: 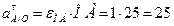см/с²;

Модуль ускорения точки А определяем по теореме Пифагора, так как векторы нормального и касательного ускорения перпендикулярны друг другу.

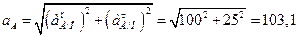см/с².

Полагая теперь, что точка А принадлежит шатуну АВ, выберем для звена АВ точку А в качестве полюса так как ее ускорение известно (Рис.77).

Для точки В можно записать:

;

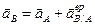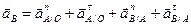
где: нормальное ускорение при вращательном движении точки В относительно точки А:

см/с²;

касательное ускорение при вращательном движении точки В относительно точки А:

.

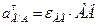При плоском движении формула определяет угловую скорость ползуна только в данный момент времени, соответствующий рассматриваемому положению механизма, поэтому угловое ускорение E не может быть получено дифференцированием по времени угловой скорости .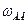

Угловое ускорение звена АВ - 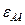неизвестно ни по величине, ни по направлению, но известно, что линия действия вектора касательного ускорения 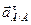перпендикулярна вектору нормального ускорения -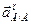

Найдем угол φ: и θ: (Рис.79): φ = γ – 90^о = 24^о; θ = 90^о – φ = 66^о;

Вводим координатные оси – ось «х» по звену АВ; ось «y» перпендикулярно звену АВ. Спроектировав векторное уравнение на координатные оси:

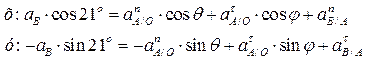
Из уравнения проекций на ось х определим ускорение точки В - а _В:

;

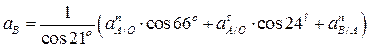Подставив значения, получим:

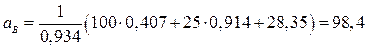см/с²;

Из проекций на ось у определим касательное ускорение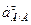

;

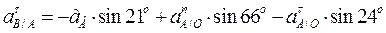Подставив значения, получим:

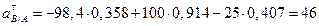см/с²;

Определим угловое ускорение звена АВ:

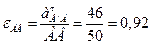с^-2.

Определим ускорение точки С:

;

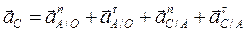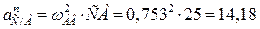см/с²;

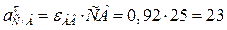см/с²;

Спроектировав векторное уравнение на координатные оси:

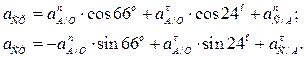
Подставив значения, получим:

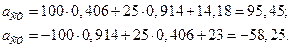
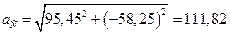см/с².

Таблица ответов:

,	,				,	,
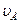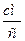
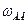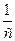
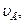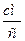
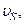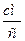
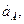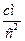
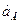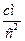
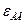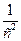
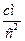
	0,753	48,7	45,72	103,1	98,4	0,92	111,82

Дата добавления: 2014-12-27