Задачи четвертого типа

Задачи третьего типа.

В некоторый момент времени известны величины и направления ускорений двух точек плоской фигуры, например, А и В. Определить в этот момент времени мгновенную угловую скорость , мгновенное угловое ускорение E и ускорение любой точки, (например, С) (см. пример19).

В некоторый момент времени известны мгновенная угловая скорость плоской фигуры 1 (или какого-либо звена), величина и направление ускорения какой-либо ее точки В (либо его можно найти из условия задачи). Некоторая точка С этой фигуры одновременно принадлежит другой фигуре (или звену), движущейся в той же плоскости. При этом ускорение какой-либо точки, например, А (пример 19) известна, (в частности, точка А может быть и неподвижной). Требуется определить угловое ускорение фигуры 1 и 2 и ускорение точки С.

Пример 22 (18.18 [9])

Антипараллелограмм (Рис.78) состоит из двух кривошипов АВ и СD одинаковой длины 40 см и шарнирно соединенного с ними стержня ВС длины 20 см. Расстояние между неподвижными осями А и D равно 20 см. Кривошип АВ вращается с постоянной угловой скоростью 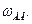Определить угловую скорость и угловое ускорение стержня ВС в тот момент времени, когда угол АDС равен 90⁰, а также определить скорость точки С и угловую скорость звена СD.

Решение

Строим схему механизма в заданном положении (Рис.78)

Рис.78

Решение

1. Определяем линейные скорости. По заданной угловой скорости кривошипа АВ находим скорость 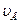точки В:

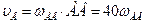
Точка В является общей для кривошипа АВ и стержня ВС, который совершает плоскопараллельное движение. Искомую угловую скорость 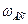стержня ВС определим с помощью мгновенного центра скоростей. Как известно для построения мгновенного центра скоростей плоской фигуры достаточно знать линии действия векторов скоростей двух ее точек. В данном случае известны линии действия векторов скоростей точек В и С (точка С кривошипа СВ описывает окружность с центром в точке D и вектор ее скорости направлен перпендикулярно радиусу CD в данный момент времени). Положение мгновенного центра скоростей (Р) находим как точку пересечения перпендикуляров, восстановленных в точках В и С к векторам их скоростей (Рис.79).

Стержень СВ вращается вокруг мгновенного центра скоростей Р с угловой скоростью 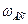. Поэтому:

Рис.79

Чтобы определить численное значение необходимо знать расстояние РВ. Для этого соединим точки В и D и рассмотрим треугольники АВС и СВD. Они имеют равные стороны и, следовательно, равные углы АВС и СВD. Если считать, что эти углы принадлежат треугольнику DРВ, то последний оказывается равнобедренным и тогда DР=РВ. Учитывая, что

РВ=АВ-АР; то есть РВ=40 - АР;

АР²=АD²+РВ²; или АР²=20²+(40 - АР)². отсюда преобразовав получим:

АР =25 см. и РВ =15 см.

Угловая скорость звена ВС:

Определяем скорость точки С учитывая, что скорость любой точки равна произведению угловой скорости звена на длину отрезка от точки до МЦС, получим:

Отрезок СР определим, зная расстояние от точки D до МЦС:

СР = СD - РD; отсюда: СР = 40-15=25 см. Тогда:

Так как точка С принадлежит кривошипу СD находим угловую скорость звена СD:

2. Определяем линейные ускорения точек и угловые ускорения звеньев.

Для определения углового ускорения E_ВС стержня ВС определяем ускорение точки В кривошипа АВ, так как закон движения кривошипа нам известен. По условию задачи кривошип вращается вокруг неподвижной оси А с постоянной угловой скоростью 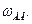Ускорение его точки В будет определяться только центростремительной (нормальной) составляющей, направленной вдоль кривошипа АВ к точке А как центру вращения кривошипа АВ (Рис.80).

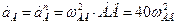
Точка В является общей для кривошипа АВ и стержня (шатуна) ВС. Выбирая точку В за полюс, представим ускорение точки С стержня ВС в соответствии с общей формулой плоского поля ускорений:

,

где: нормальное ускорение:

- известно по величине и направлению, и его модуль: ;

- касательное ускорение:

- известно только по линии действия.

Учтем, что точка С принадлежит и кривошипу СD, который вращается вокруг неподвижной оси, проходящей через точку D, поэтому:

,

где: нормальное ускорение:

- известно по величине и направлению, его модуль: ;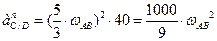

касательное ускорение:

- известно только по линии действия.

Приравнивая правые части этих равенств, получим векторное уравнение:

.

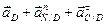Проектируя полученное векторное уравнение на координатные оси х и у (Рис.80) получим:

;

.

Из первого уравнения (проекции на ось х) получим:

;

Из второго уравнения (проекции на ось у) получим:

Рис.80

Из треугольника СВР (рис.79):

; ; ; .

Подставив значения, получим:

;

Знак «минус» у касательного ускорения говорит о том, что вектор направлен в сторону, противоположную обозначенному направлению на чертеже (Рис.81). Зная касательное ускорение можно определить угловое ускорение звена СD:

;

Определяем касательное ускорение :

;

Подставив значения, получим:

.

Зная касательное ускорение можно определить угловое ускорение звена СВ:

Для определения ускорения точки С, записав проекции векторного уравнения на координатные оси х и у, получим:

,

.

Подставив значения, получим:

;

.

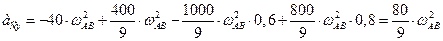
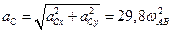Дата добавления: 2014-12-27