Для однородной линии с распределенными параметрами

Составление дифференциальных уравнений

Электрическими цепями с распределенными параметрами будем называть такие цепи, в которых ток и напряжение непрерывно изменяются при переходе от одной точки (сечения) цепи к другой (соседней) точке.

Цепи с распределенными параметрами

Термин «цепи с распределенными параметрами» обычно связывают с мощными линиями передачи электрической энергии на большие расстояния, телефонными и телеграфными воздушными и кабельными линиями, рельсовыми линиями автоблокировки на железнодорожном транспорте, антеннами в радиотехнике и другими родственными линиями и установками. Поэтому часто их определяют термином «линии с распределенными параметрами».

В то же время устройства с распределенными параметрами встречаются и тогда, когда «линий» в буквальном смысле этого слова, казалось бы, вовсе нет. Так, обычная индуктивная катушка представляет собой при повышенной частоте линию с распределенными параметрами. Действительно между каждыми двумя соседними витками катушки, как и между каждыми двумя телами, есть емкость. Кроме того, каждый виток обладает емкостью на корпус прибора или на землю.

Если по катушке будет протекать переменный ток, то через межвитковые емкости и емкости на землю потечет ток. При одном и том же напряжении между соседними витками ток через емкости будет тем большем, чем выше частота переменного тока. При низкой частоте (десятки, сотни, тысячи герц) ток через емкости будет небольшим по сравнению с токами через витки катушки, и наличие емкостей можно не учитывать в расчете, что и делалось до сих пор. Если же частота тока будет очень большой, например будет достигать миллионов герц, то токи через емкости могут во много раз превышать токи через витки катушки. В этом случае вся катушка в целом будет оказывать прохождению переменного тока емкостное, а не индуктивное сопротивление – количество перешло в новое качество. При промежуточных частотах около сотен килогерц индуктивная катушка, если не принято специальных мер, представляет собой типичную линию с распределенными параметрами. Если индуктивная катушка намотана на стальной сердечник, который способен насыщаться, и частота тока достаточно большая, то все устройство в целом представляет собой сложную совокупность из электрической и магнитной нелинейных цепей с распределенными параметрами.

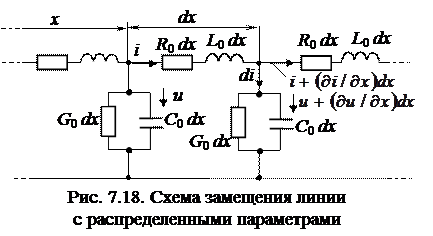Рассмотрим длинную линию связи (или электропередачи). У нее изменяется сопротивление, индуктивность и емкость при изменении длины. Разобьем линию на участки длиной dx (рис. 7.18); x – это расстояние, отсчитываемое от начала линии. На длине dx активное сопротивление равно R ₀ dx, индуктивность L ₀ dx, проводимость утечки G ₀ dx и емкость C ₀ dx.

Пусть R ₀ – продольное активное сопротивление единицы длины линии, L ₀ – индуктивность единицы длины линии, C ₀ – емкость единицы длины линии и G ₀ – поперечная проводимость единицы длины линии. Отметим, что поперечная проводимость G ₀ не является обратной величиной по отношению к продольному сопротивлению R ₀.

Обозначим ток в начале рассматриваемого участка линии

через i, а напряжение между проводами линии в начале участка – u. И ток, и напряжение являются в общем случае функциями расстояния вдоль линии x и времени t. Поэтому в дальнейшем в уравнениях будут участвовать частные производные от u и i по времени t и расстоянию x.

Если для некоторого момента времени t ток в начале рассматриваемого участка равен i, то вследствие наличия утечки тока через поперечный элемент ток в конце участка для того же момента времени будет равен i+(дi/дx)dx, где дi/дx – скорость изменения тока в направлении x. Эта скорость, умноженная на расстояние dx, дает приращение тока на пути dx. Аналогично, если напряжение в начале участка u, то в конце участка для того же момента времени напряжение равно u+(дu/дx)dx.

Составим уравнение по второму закону Кирхгофа для замкнутого контура, образованного участком линии длиной dx, обойдя его по часовой стрелке:

–u+iR ₀ dx+L ₀ dx(дi/дt)+u+(дu/дx)dx=0.

После упрощения и деления уравнения на dx получим

– дu/дx=L ₀ дi/дt+R ₀ i. (7.9)

По первому закону Кирхгофа

i=di+ i+ (дi/дx)dx. (7.10)

Ток di (рис. 7.21) равен сумме токов, проходящих через проводимость G ₀ dx и через емкость C ₀ dx:

di=[u+(дu/дx)dx]G ₀ dx+)C ₀ dx ∙ д[u+(дu/дx)dx] /дt.

Пренебрегаем слагаемыми второго порядка малости, тогда

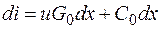(дu/дt). (7.11)

Подставим (7.11) в (7.10), упростим и поделим полученное уравнение на dx:

–дi/дx=G ₀ u + C ₀ (дu/дt). (7.12)

Уравнения (7.9) и (7.12) являются основными дифференциальными уравнениями для линии с распределенными параметрами.

Дата добавления: 2014-12-27