Вторичные параметры четырехполюсников

В качестве вторичных параметров четырехполюсников используют характеристические сопротивления Z_{С 1}, Z_{С 2} и постоянную передачи g. Для симметричного четырехполюсника Z _{C 1} = Z _{C 2} = Z _C. Характеристическое сопротивление Z _C равно такому сопротивлению нагрузки Z _C= Z _H,при котором входное сопротивление четырехполюсника равно этому сопротивлению Z _вх= Z _C. Так как у симметричного четырехполюсника A = D и 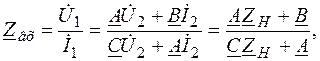то, подставляя Z _вх= Z _C и Z _H= Z _C, получим 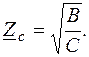Режим работы, при котором сопротивление нагрузки равно характеристическому сопротивлению четырехполюсника, называют согласованным режимом. В большинстве практических задач он является желательным.

Для несимметричного четырехполюсника характеристическое сопротивление со стороны входа Z_C1 связано с таким сопротивлением нагрузки, равном сопротивлению Z_C2 , при котором входное сопротивление равно Z_C1.Для Z_C2 сопротивления связаны аналогично. При этом Z _C1= √AB/CD = √Z_1хх Z_1k и соответственно Z _C2= √BD/AC = √Z_2хх Z_2k

Постоянная передачи g является комплексным числом g =a+jb. При этом

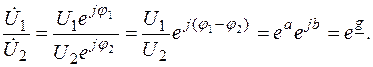
Единица коэффициента фазы b=j ₁ –j ₂ радиан, а коэффициента затухания 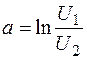непер (Нп) или белл (Б). Затуханию в 1 Нп соответствует отношение напряжений U ₁ /U ₂ =e ¹ = 2,73. При определении затухания в беллах (или децибеллах) используют десятичные логарифмы 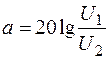(дБ). При этом затуханию в 1 Белл соответствует затухание в 1,15 Непера.

Постоянная передачи симметричного четырехполюсника может быть определена через А -параметры

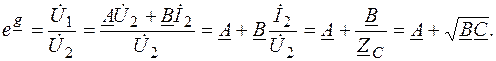
Аналогичным образом можно определить А -коэффициенты симметричного четырехполюсника через вторичные параметры Z _C и g.

Дополняя предыдущее уравнение уравнением AD – BC = 1 и принимая A = D, получим из первого уравнения 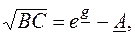и из второго BC=A ² – 1. После возведения в квадрат и приравнивая BC по одному и другому выражению получаем

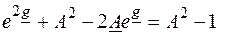или .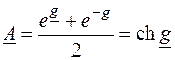

Подставив значение A в ранее полученное выражение 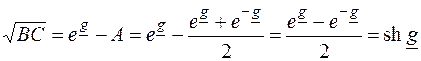и учитывая 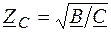, определим B = Z _C sh g, 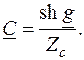При этом уравнения симметричного четырехполюсника через вторичные параметры имеют вид

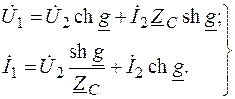. (7.4)

Входное сопротивление симметричного четырехполюсника

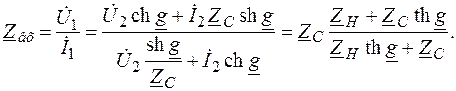
При коротком замыкании U ₂ = 0 Z _k= Z _C th g.

При холостом ходе I ₂ = 0 Z _xx= Z _C/ th g.

Измерив опытным путем сопротивление четырехполюсника в режимах холостого хода и короткого замыкания, определим по двум последним уравнениям вторичные параметры

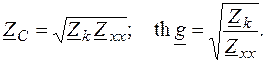(7.5)

П р и м е р 7.2. Три симметричных четырехполюсника, имеющих параметры Z_C и g, соединены каскадно (последовательно один за другим). Определить входное сопротивление и постоянную передачи каскада, если сопротивление нагрузки Z _H= Z _C.

Р е ш е н и е.

1. Учитывая, что входное сопротивление четырехполюсника при согласованном режиме включения, т.е. при Z _H = Z _C, также равно Z _вх= Z _C, получим, что все три четырехполюсника оказались включенными в согласованном режиме и входное сопротивление каскада тоже равно Z _{вх общ}= Z _C.

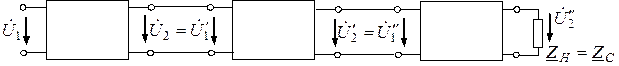
Рис. 7.4. Схема к примеру 7.2

2. Так как выходное напряжение 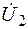первого каскада является входным напряжением второго каскада (рис. 7.4), т. е. 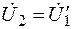и аналогично 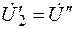, то

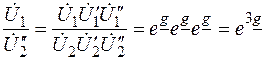или .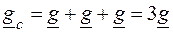

Дата добавления: 2014-12-27