Параметрами при установившемся синусоидальном процессе

Решение уравнений линии с распределенными

Пусть напряжение и ток в линии изменяются по синусоидальному закону во времени. Воспользуемся символическим методом.

Изображением тока i = I_m sin (wt + j_i) является комплекс ,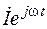

где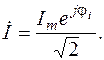

Изображением напряжения 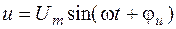является комплекс 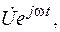где

Комплексы и 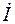являются функциями расстояния x, но не функциями времени. Множитель e^jwt – функция времени t, но не зависит от x.

Представление изображения тока и изображения напряжения в виде произведения двух множителей, из которых один является функцией только x, а другой – функцией только t, дает возможность перейти от уравнений в частных производных [уравнений (7.9) и (7.12)] к уравнениям в простых производных.

Действительно,

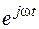
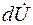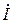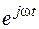дu/дx → /dx; L ₀ (дi/дt)→L ₀ д /дt= 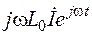; (7.13.)

дi/дx → 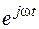d 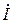/dx;С₀(дu/дt)→ 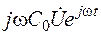. (7.14)

Подставим (7.13) и (7.14) в 7.9) и в (7.12) и сократим в полученных уравнениях множитель e ^jωt. Получим

(7.15)

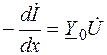, (7.16)

где Z ₀ =R ₀ +jωL ₀; (7.17)

Y ₀ =G ₀ +jωC ₀.(7.18)

Решим систему уравнений (7.15.) и (7.16) относительно . С этой целью продифференцируем выражение (7.15) по x:

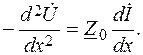(7.19)

В уравнение (7.19) вместо 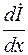подставим правую часть уравнения (7.16). Получим

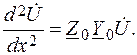(7.20)

Уравнение (7.20) представляет собой линейное дифференциальное уравнение второго порядка. Решение его

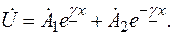(7.21)

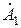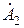Комплексные числа и – постоянные интегрирования, которые в дальнейшим определим через напряжение и ток в начале линии или через напряжение и ток в конце линии.

Коэффициент 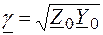(7.22)

принято называть постоянной распространения;

g – комплексное число, потому его можно представить в виде

γ =α+jβ,(7.23)

где α – коэффициент затухания, β – коэффициент фазы.

Коэффициент затухания α характеризует затухание падающей волны на единицу длины линии (на 1 км), а коэффициент фазы β – изменение фазы падающей волны на единицу длины линии. Ток 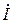определим из уравнения (7.15):

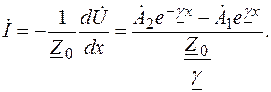(7.24)

Величину обозначают Z _C и называют волновым сопротивлением

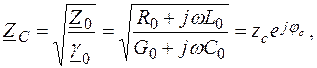(7.25)

где z_c – модуль; φ_c – аргумент волнового сопротивления Z_C.

Следовательно,

(7.26)

Обозначим расстояние от текущей точки на линии до конца линии через у и длину всей линии через l:

(7.27)

Пусть будут известны напряжение и ток в конце лини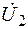и и 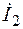. Подставим в формулы (7.21) и (7.24) x = l, 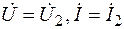и составим уравнения для определения постоянных интегрирования 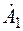и :

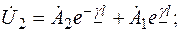
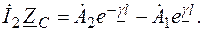
Отсюда

(7.28)

Если подставить уравнения (7.28) в (7.21) и (7.26), заменить l – x на у и перейти к гиперболическим функциям, получим

(7.29)

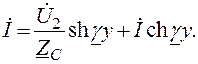(7.30)

Формулы (7.29) и (7.30)позволяют, зная 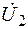и 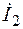,определить комплексы напряжения и тока в точке, находящейся на расстоянии у от конца линии.

Для режима холостого хода (I ₂ = 0) определим, пользуясь уравнениями (7.29) и (7.30), сопротивление линии 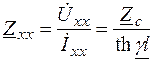. Аналогично для режима короткого замыкания (U ₂ = 0) определим . Перемножив левую и правую части последних формул, определим 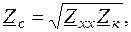а разделив, получим 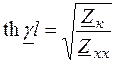. Постоянную распространения γ определим из последнего уравнения: ,

.

Зная волновое сопротивление и постоянную распространения, можно определить первичные параметры линии

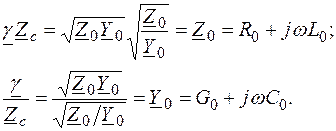
Дата добавления: 2014-12-27