Определение напряжения и тока в линии без потерь

Линий без потерь не существует. Однако можно создать линию с очень малыми потерями (с очень малыми R ₀ и G ₀) и распространить на нее теорию линий без потерь.

Из предыдущего [см. формулы (7.17) (7.18) (7.23) (7.22)] известно, что если

R ₀ = G ₀ = 0, то

т.е. коэффициент затухания α = 0, а коэффициент фазы

При этом волновое сопротивление Z _C является чисто активным [см. формулу (7.25)] и равно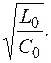

Для определения напряжения и тока 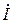в любой точке линии обратимся к формулам (7.29) и (7.30).

Повторим их: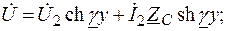

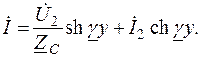
Учтем, что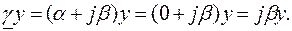

Гиперболический синус от мнимого аргумента jx равен произведению j на круговой синус от аргумента x:

Следовательно,

Аналогично можно показать, что гиперболический косинус от мнимого аргумента jx равен круговому косинусу от аргумента x, т.е

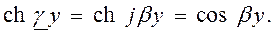
Поэтому для линии без потерь формулы (7.29) и (7.30) перепишем следующим образом:

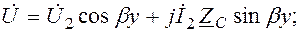(7.36)

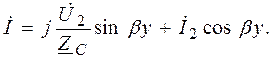(7.37)

При холостом ходе I ₂ = 0, тогда

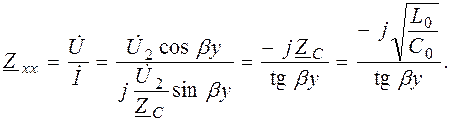(7.38)

Исследуем характер изменения Z _хх при изменении расстояния y от конца линии до текущей точки на ней.

В интервале значений βy от 0 до π /2 tg βy изменяется от 0 до ¥, поэтому Z _хх имеет в соответствии с уравнением (6.30) емкостный характер (множитель – j) и по модулю изменяется от ¥ до 0. В интервале значений βy от 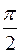до p tg βy отрицателен и изменяется от – ¥ до 0, поэтому Z _хх изменяется по модулю от 0 до ¥ и имеет индуктивный характер (множитель + j) и т.д. Таким образом, изменяя длину отрезка линии без потерь, можно имитировать любое емкостное и индуктивное сопротивления. Практически это свойство используется при высокой частоте в различных радиотехнических установках.

При коротком замыкании на конце линии U ₂ = 0 и из формул (7.36) и (7.37) следует, что входное сопротивление

, где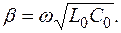

Будем менять длину отрезка линии y и исследуем характер изменения входного сопротивления.

В интервале значений βy от 0 до π /2 tg βy положителен и изменяется от 0 до ¥; следовательно, в этом интервале входное сопротивление имеет индуктивный характер и по модулю изменяется от 0 до ¥.

В линиях без потерь при холостом ходе, при коротком замыкании, а также при чисто реактивных нагрузках образуются так называемые стоячие электромагнитные волны.

Стоячая электромагнитная волна представляет собой электромагнитную волну, полученную в результате наложения движущихся навстречу падающей и отраженной электромагнитных волн одинаковой интенсивности.

Точки линии, где периодическая функция координаты проходит через нуль, называются узлами, а точки линии, в которых периодическая функция координаты принимает максимальные значения, – пучностями (рис. 7.20).

При возникновении стоячих волн электромагнитная энергия от начала линии к концу линии не передается.

Однако на каждом отрезке линии, равном четверти длины волны, запасена некоторая электромагнитная энергия, которая периодически переходит из одного вида в другой вид (из энергии электрического поля, в энергию магнитного поля).

В те моменты времени, когда ток вдоль всей линии оказывается равным нулю, а напряжение достигает максимального значения, вся энергия перешла в энергию электрического поля.

В те моменты времени, когда напряжение вдоль всей линии равно нулю, а ток максимален, вся энергия перешла в энергию магнитного поля.

Из формул (7.35) и (7.37) следует, что при холостом ходе

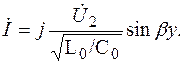(7.39)

Для перехода к функциям времени умножим правые части двух последних формул на 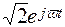и от полученных произведений возьмем мнимые части:

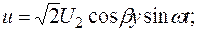
Угол 90^° в аргументе у синуса в последней формуле соответствует множителю j в формуле комплекса тока.

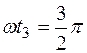В точках ay = kp, где k =0, 1, 2.., будут узлы тока и пучности напряжения. График стоячих волн напряжения и тока для трех смежных моментов времени wt = 0, и показан на рис. 7.20; на верхнем графике – напряжение, на нижнем – ток.

Утолщенными линиями показана волна при wt ₁ = 0, тонкими линиями – при ωt ₂ = p /2 пунктирными – при ωt ₃ = 3 p /2 для напряжения и при wt = p для тока.

Из тех же формул следует, что при коротком замыкании на конце линии (U₂ = 0)

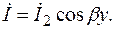(7.40)

Для перехода к мгновенным значениям умножим правые части двух последних формул на 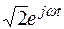и от произведений возьмем мнимые части:

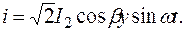
Следовательно, картина стоячей волны напряжения при коротком замыкании на конце линии качественно повторяет картину стоячей волны тока при холостом ходе линии.

Аналогично картина стоячей волны тока в короткозамкнутой линии качественно повторяет картину стоячей волны напряжения при холостом ходе линии.

При перемене местами источника и нагрузки в схеме линии с распределенными параметрами токи в источнике и нагрузке не изменяются.

Таким же свойством обладает симметричный четырехполюсник, поэтому однородная линия с распределенными параметрами может быть заменена симметричным четырехполюсником и, обратно, симметричный четырехполюсник можно заменить участком однородной линии с распределенными параметрами.

Дата добавления: 2014-12-27