Разностные уравнения

Аналогом первой производной обычной непрерывной функции является дискретная функция, называемая первой разностью

.

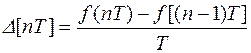Аналогом второй производной является вторая разность

.

Также определяют разности более высоких порядков. При этом, естественно, единичный дискретный импульс является первой разностью от дискретной ступенчатой функции, т.е.

d (nT)=1(nT)–1[(n– 1) T ]=D1(nT).

Подобно дифференциальному уравнению получают разностные уравнения. Так, для цепи RC в соответствии с уравнением iR+u_C=e или 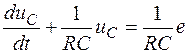при t > 0 получим

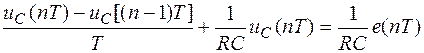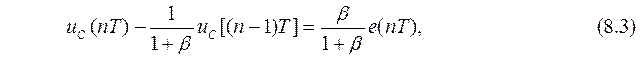, где β = T/RC.

Разностные уравнения обычно бывают рекуррентными. Значения реакции можно вычислять последовательно, задавая n =0,1,2,3... и используя при этом значения входного воздействия e (nT) и начальные значения искомой величины u_С (– T). Так, для цепи RC, используя полученное разностное уравнение и данные:

e (nT)= d (nT)+2 d [(n– 1) T ], RC =4, b =0,25; T =1; u_С (– T)=1, получим:

при n =0 u_C (0)=0,8 u_C (–1)+0,2 d (0)=1,

при n =1 u_C (1)=0,8 u_C (0)+0,4 d (0)=0,8+0,4=1,2,

при n =2 u_C (2)=0,8 u_C (1)=0,8×1,2=0,96,

при n =3 u_C (3)=0,8 u_C (2)=0,8×0,96=0,786.

Для разностных уравнений более высоких порядков необходимо знать больше начальных разностей, т.е. для уравнений второго порядка необходимы f (– T) и f (–2 T), для третьего порядка – f (– T), f (–2 T), f (–3 T) и т. д.

Разностные уравнения используются при решении обычных дифференциальных уравнений на ЭВМ. При этом интересующий промежуток времени разбивают на малые интервалы (шаги) D t = T и определяют дискретные значения искомой величины C (nT). Имеется много алгоритмов решения разностных уравнений. Наиболее часто применяют алгоритм Рунге-Кутта четвертого порядка. Отметим, что для сложных электрических цепей, содержащих много реактивных элементов, необходимо составлять дифференциальные уравнения методом переменных состояния. Это требует значительного времени на подготовку этих уравнений.

Дата добавления: 2014-12-27