Цифровые модели

Реакцию цепи или системы с нулевыми начальными условиями на воздействие единичного дискретного импульса называют дискретной импульсной характеристикой h^δ (nT). Ее определяют обычно из разностных уравнений, например для уравнения (8.1) при Т =1, b =0.25, U_С (– T)=0 определим

h^δ (nT) =u_C (nT) = 0.8 u_C [(n– 1) T ]+0.2 d (nT).

Принимая n= 0,1,2,3, получим u_C (nT) = 1; 0,8; 0,64; 0,512…и соответственно

h^δ (nT) =d (nT)+0.8 u_C [(n– 1) T ]+0.64 d [(n– 2) T ]+…

Аналогично записи интеграла Дюамеля для аналогового сигнала

f ₂ (t)=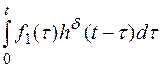

можно записать для цифрового сигнала

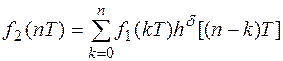(8.4)

Полученное выражение, называемое дискретной сверткой, является аналогом интегралов наложения для непрерывных сигналов. На основе этого уравнения выполняют цифровое моделирование аналоговых процессов. Для этого аналоговый сигнал f ₁(t) заменяют дискретным f ₁(nT), приняв достаточно малый шаг дискретизации Т. Зная импульсную характеристику h^δ (nT) устройства или исследуемой цепи, по уравнению (2) определяют дискретный сигнал f ₂(nT). Например, задан дискретный сигнал (рис. 8.3, а) при нулевых начальных условиях f ₁(nT) = 2 d (nT)+3 d [(n– 3) T ]–2 d [(n– 5) T ] и дискретная импульсная характеристика (рис. 8.3, б) h ^δ(nT) = 2 d (nT)+ d [(n– 1) T ]+0,5 d [(n– 2) T ].

Реакцию цепи на f ₁(nT) определим, используя наложение (рис. 8.3, в)

f ₂(nT) =f ₁(0) h ¢(nT)+ f ₁(T)× h ¢[(n– 1) T ]+… = 2 h ¢(nT)+3 h ¢[(n– 3) T ]–2 h ¢[(n– 5) T ]+… =

= 4 d (nT)+2 d [(n– 1) T ]+ d [(n– 2) T ]+6 d [(n– 3) T ]+3 d [(n– 4) T ]–2,5 d [(n– 5) T ]–2 d [(n– 6) T ]–– d [(n– 7) T ], так как дискретный импульс d (nT) вызывает реакцию цепи h^δ (nT), а смещенный на mT дискретный импульс d [(n–m) T ] вызовет реакцию h^δ [(n–m) T ].

8.4. Z -преобразование цифровых сигналов

Эффективным методом решения разностных уравнений является так называемое z -преобразование.

Пусть задан дискретный сигнал, записанный через смещенные дискретные импульсы,

.

Прямым z-преобразованием этой последовательности называют ряд по обратным степеням комплексной переменной z, сходящийся для всех ï z ï>1,

.

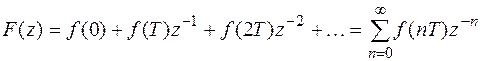Это z -преобразование получают формально припиской к значению последовательности в точке kT множителя z^–k (вместо сомножителя d [(n – k) T ]). Так, для конечной последовательности f [ nT ]: 2, 3, 1, 0, –2 сразу записываем F (z)=2+3 z^{– 1}+ z^{– 2}–2 z^{– 4}.

Также легко перейти обратно от z -изображения к временной последовательности заменой z смещенным на kT дискретным импульсом. Так, для выражения F (z)=4+5 z^{– 1}+3 z^{– 3}– z^{– 4} сразу записываем f (nT)=4 d (nT)+5 d [(n– 1) T ]+3 d [(n– 3) T ]– d [(n– 4) T ].

Таким образом, z -преобразование аналогично преобразованиям Лапласа – имеем оригинал f (nT) и его изображение F (z).

Иногда используют преобразование переменной p = σ +jω в другую комплексную переменную z = х + jy по правилу

z = exp(pT) = exp(σT) exp(jωT) = x + jy,

где х = exp(σT)cos(ωT); у = exp(σT)sin(ωT).

При преобразовании параметра р в параметр z мнимая ось комплексной плоскости jω преобразуется в окружность с радиусом

R = ехр (σT), левая полуплоскость p – во внутреннюю область, а правая – во внешнюю область этой окружности.

Рассмотрим z -изображения некоторых дискретных функций времени.

А. Дискретный импульс d (nT) состоит только из одной выборки единичного значения при n =0, остальные значения при n ¹0 равны нулю, поэтому f (nT)= d (nT)«F (z)=1.

Аналогично смещенный на kT дискретный импульс содержит одну выборку единичного значения при n=k

f (nT)= d [(n – k) T ]«F(z)= z^–k.

Б. Дискретная ступенчатая функция, имеющая постоянные значения при всех n ³0,

.

В. Геометрическая прогрессия

f (nT)= d (nT)+ ad [(n –1)]+ a ² d [(n –2) T ]+...

имеет изображение

.

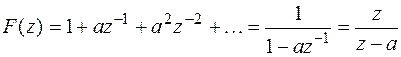Г. Дискретная экспонента f (nT)= e^–aTn, представляющая собой последовательность выборок функции e^–at, имеет изображение, аналогичное предыдущему, так как является тоже геометрической прогрессией

.

Если исходный аналоговый сигнал состоит из суммы экспонент 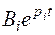, то изображение этого сигнала тоже будет суммой:

.

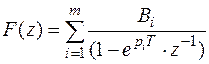При дробно-рациональных изображениях применяют разложение на простые дроби отношения F (z)/ z, которое является правильной дробью, например изображение

можно представить в виде

.

Здесь корни знаменателя H (z)=0 z = 0,5 и z = 0,25. Тогда

.

Оригинал этого выражения получится в виде суммы геометрических прогрессий .

При n =0 получим f (0)=3, при n =2 получим

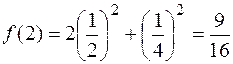и т. д.

Такой прием похож на известную в операторном методе теорему разложения.

Аналогично известной в операторном методе теореме смещения существует теорема смещения (сдвига) для z -преобразований. Суть ее в следующем. Если последовательность f (nT), равная нулю при n <0, имеет преобразование F (z), то последовательность f ₁(nT)= f [(n – m) T ], полученная смещением исходной последовательности на mT, будет иметь изображение F (z)= z^–mF (z). Таким образом, умножение функции F (z) на z^–m означает ее задержку на m интервалов дискретизации T. При смещении на 1 интервал (m =1) получим, учитывая формулу для смещения дискретного импульса,

F ₁(z)= f (– T)+ f (0) z ^–1+ f (T) z ^–2+…= f (– T)+ z ^–1 F (z),

при смещении на 2 интервала (m =2) получим

F ₁(z)= f (–2 T)+ f (– T) z ^–1+ f (0) z ^–2+…= f (–2 T)+ f (– T) z ^–1+ z ^–2 F (z).

Дата добавления: 2014-12-27