Алгоритм вычисления

1. Составить таблицу.

№ испытуемых п/п	Результат “до” тренинга	Результат “после” тренинга	Сдвиг

В столбец 1 внести номер испытуемых.

В столбец 3 внести результаты первичного обследования.

В строку 3 внести результаты повторного обследования.

2. Вычислить величину сдвига, то есть разницу между результатом «после» и «до» проведения развивающей работы.

3. Подсчитать количество нулевых, положительных и отрицательных сдвигов, причем нулевые сдвиги отбрасываются.

4. Определить сумму типичных (наиболее встречаемых) сдвигов и обозначить их буквой n. Подсчитать количество нетипичных сдвигов и обозначить их G ‘эмп.

5. Провести оценку статистической значимости по таблице. Обозначить полученный результат на «оси значимости».

6. Сделать вывод л наличии или отсутствии различий в полученных результатах.

Задача 6.1.

Психолог проводит групповой тренинг. Его задача – выяснить будет ли эффективен данный конкретный вариант тренинга для снижения уровня тревожности участников?

Решение. Для решения этой задачи психолог с помощью теста Тейлора дважды выявляет уровень тревожности у 14 участников до и после проведения тренинга. Результаты измерения приведем в таблице 6.1, включив в нее столбец, необходимый для расчета по критерию знаков G.

Таблица 6.1.

№ испытуемых п/п	Уровень тревожности “до” тренинга	Уровень тревожности “после” тренинга	Сдвиг
			+4
			-9
			-1
			-6
			+5
			+3
			+1
			+1
			+1
			-1
			-7
			+2
			+3

В столбце, обозначенном словом “Сдвиг”, для каждого участника отдельно определяют, насколько изменился его уровень тревожности после проведения тренинга. Сдвиг – это величина разности между уровнями тревожности одного и того же участника “ после” и “до” тренинга. Но не наоборот! Величины сдвигов обязательно должны быть даны в соответствующем столбце таблице с учетом знаков.

В критерии знаков по результатам, полученным в столбце таблицы, обозначенном словом “Сдвиг”, подсчитываются суммы нулевых, положительных и отрицательных сдвигов. При использовании критерия знаков необходимо учитывать только сумму положительных и отрицательных сдвигов, а сумму нулевых – отбрасывать.

Проведем необходимый подсчет для нашей задачи:

общее число (сумма) нулевых сдвигов = 1;

общее число (сумма) положительных сдвигов = 8;

общее число (сумма) отрицательных сдвигов = 5.

Таким образом, отбросив нулевые сдвиги, получаем 13 ненулевых сдвигов. При этом подсчет показал, что сдвиги имели место и что большая часть из них положительна.

Напомним, что критерий знаков G предназначен для установления того, как изменяются значения признака при повторном измерении связной выборки: в сторону увеличения или уменьшения. Поэтому, анализируя соотношение положительных и отрицательных сдвигов в нашей задаче, решаем вопрос: можно ли утверждать, что после проведения тренинга наблюдается достоверный сдвиг в сторону уменьшения уровня тревожности участников?

Для решения этого вопроса необходимо ввести два обозначения.

Первое – сумма сдвигов, получившаяся наибольшей, носит название типичного сдвига и обозначается буквой п. Типичный сдвиг используется при работе с таблицей, в которой приводятся критические величины 5 % и 1 % уровней значимости данного критерия.

Второе – сумма сдвигов, получившаяся наименьшей, носит название – нетипичного сдвига и обозначается как – G эмп. Эта величина (G эмп) располагается на “оси значимости”. В нашем случае G эмп = 5. В целом типичный и нетипичный сдвиги рассматриваются как дополнительные друг к другу.

Подчеркнем, что в том случае, когда величины типичного и нетипичного сдвигов оказываются равными, критерий знаков неприменим.

Оценка статистической достоверности различий по критерию знаков производится по таблице. В ней в столбце, обозначенном буквой n приведены величины типичных сдвигов, а в столбцах, имеющих обозначение, соответствующее уровнями значимости Р = 0,05 и Р = 0,01, – так называемые критические величины. Условно их также можно считать нетипичными сдвигами. Они обозначаются, как G кри с ними сравнивается полученное значение нетипичного сдвига G эм п.

Итак, оцениваем уровень достоверности различий нашей задачи. Для этого необходимо воспользоваться таблицей. Поскольку в нашем примере n = 8, (это число типичных сдвигов), поэтому нужный нам участок таблицы 1 Приложения выглядит так:

Таблица 6.2

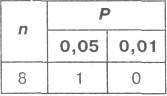
Более компактно соответствующую строчку таблицы 1 Приложения принято записывать следующим образом:

Эта запись означает, что при уровне значимости в 5 %, сумма нетипичных сдвигов не должна превышать 1, а при уровне значимости в 1 % – 0. В нашем случае G эмп = 5, что существенно больше 1.

Для большей наглядности следует построить так называемую “ось значимости”, на которой располагаются как величины критических сдвигов, так и величина G эмп, т.е. величина нетипичного сдвига.

“Ось значимости” имеет следующий вид:

Использование “оси значимости” позволяет отчетливо видеть, что G эмп попало в зону незначимости, т.е. полученный в эксперименте общий положительный сдвиг, который соответствует увеличению уровня тревожности испытуемых после проведения тренинга, статистически недостоверен. Иначе говоря, данный способ воздействия не привел к существенным изменениям в уровне тревожности испытуемых.

Обращаем внимание, что в критерии знаков “ось значимости” образно говоря, перевернута. Нуль располагается не как обычно (на числовой оси слева), а справа и увеличение числового ряда идет в противоположную сторону, т.е. справа налево. Последнее связано с тем, что чем больше количество нетипичных сдвигов, тем меньше вероятность того, что суммарный сдвиг окажется статистически достоверен. Подобные исключения в направленности “оси значимости” будут встречаться и далее.

Полученный выше результат может быть переформулирован также в терминах нулевой и альтернативной гипотез: поскольку преобладание типичного положительного направления сдвига в данном конкретном эксперименте является случайным, то должна быть принята гипотеза Н0 об отсутствии различий, или о наличии сходства. Возвращаясь к психологической задаче, укажем, что, согласно критерию знаков, примененный психологом способ тренинга неудовлетворителен, поскольку не дает статистически достоверных изменений в состоянии участников тренинга.

6.2.2. Парный критерий Т – Вилкоксона

Для решения задач, в которых осуществляется сравнение двух рядов чисел, кроме критерия знаков G психолог может использовать парный критерий Т– Вилкоксона. Этот критерий является более мощным, чем критерий знаков, и применяется для оценки различий экспериментальных данных, полученных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет выявить не только направленность изменений, но и их выраженность, т.е. он позволяет установить, насколько сдвиг показателей в каком-то одном направлении является более интенсивным, чем в другом.

Критерий Т основан на ранжировании абсолютных величин разности между двумя рядами выборочных значений в первом и втором эксперименте (например “до” и “после” какого-либо воздействия). Ранжирование абсолютных величин означает, что знаки разностей не учитываются, однако в дальнейшем наряду с общей суммой рангов находится отдельно сумма рангов как для положительных, так и для отрицательных сдвигов. Если интенсивность сдвига в одном из направлении оказывается большей, то и соответствующая сумма рангов также оказывается больше. Этот сдвиг, как и в случае критерия знаков, называется типичным, а противоположный, меньший по сумме рангов сдвиг – нетипичным. Как и для критерия знаков эти два сдвига оказываются дополнительными друг к другу. Критерий Т – Вилкоксона базируется на величине нетипичного сдвига, который называется в дальнейшем Т эмп.

Для применения критерия Т Вилкоксона необходимо соблюдать следующие условия:

1. Измерение может быть проведено во всех шкалах, кроме номинальной.

2. Выборка должна быть связной.

3. Число элементов в сравниваемых выборках должно быть равным.

4. Критерий Т – Вилкоксона может применяться при численности выборки от 5 до 50 (на большую величину не рассчитана таблица достоверности).

Алгоритм вычисления.

1. Результаты обследования заносятся в таблицу.

№ испытуемых п/п	До	После	Сдвиг (значение разности с учетом знака)	Абсолютные величины разностей	Ранги абсолютных величин разностей	Символ нетипичного сдвига

В столбец 1 вносится номер испытуемого. Столбец 2 – первичные результаты обследования, а в столбец 3 – результаты повторного обследования.

2. В столбце 4 вносятся результаты сдвига, то есть разница между результатом после и до обследования с соответствующим знаком. Их вычисляют путем вычитания из чисел третьего столбца соответствующих чисел второго столбца.

3. В столбце 5 записывается абсолютная величина разностей сдвигов (при этом знак «-» - убирается).

4. В. столбце 6 высчитывается ранг абсолютных величин разностей.

5. Подсчитывается сумма рангов по формуле (1.1):

6. В столбце 7 отмечаются нетипичные сдвиги (на основе результатов представленных в столбце 4)

7. Суммируются ранги нетипичных сдвигов. Это и есть искомый результат Т эмп.

8. Проводится оценка статистической значимости по таблице по общему числу испытуемых. Результат обозначается на «оси значимости».

9. Делается вывод о наличии или отсутствии различий в полученных результатах.

Задача 6.3.

Психолог проводит с младшими школьниками коррекционную работу по формированию навыков внимания, используя для оценки результатов корректурную пробу. Задача состоит в том, чтобы определить, будет ли уменьшаться количество ошибок внимания у младших школьников после специальных коррекционных упражнений?

Решение. Для решения этой задачи психолог у 19 детей определяет количество ошибок при выполнении корректурной пробы до и после коррекционных упражнений. В таблице 6.5 приведены соответствующие экспериментальные данные и дополнительные столбцы, необходимые для работы по парному критерию Т – Вилкоксона.

Таблица 6.5

№ 1	№ 2	№ 3	№ 4	№ 5	№ 6	№ 7
№ испытуемых п/п	До	После	Сдвиг (значение разности с учетом знака)	Абсолютные величины разностей	Ранги абсолютных величин разностей	Символ нетипичного сдвига
			-2		10,5
			-1		6,5
			+1		6,5	*
			-8
			-11
			-20
			-18
			-1		6,5
			+1		6,5	*
			-22
			-1		6,5
			-2		10,5
			-6		13.5
			-4
			-1		6,5
			+6		13,5	*
сумма						Т эмп -26,5

Обработка данных по критерию Т – Вилкоксона осуществляется следующим образом:

1. В четвертый столбец таблицы 6.5 вносятся величины сдвигов с учетом знака.

2. В пятом столбце в соответствие каждому значению сдвига ставят его абсолютную величину.

3. В шестом столбце ранжируют абсолютные величины сдвигов, представленных в пятом столбце.

4. Подсчитывают сумму рангов. В нашем примере она составляет: 12,5 + 6,5 + 6,5 + 15 + 16 + 2 + 18 + 17 + 6,5 + 6,5 + 19 + 6,5 + + 10,5 + 13,5 + 12 + 6,5 + 13,5 + 2 = 190

5. Проверяют правильность ранжирования на основе совпадения сумм рангов полученных двумя способами. В нашем случае обе величины совпали, 190 = 190, следовательно, ранжирование проведено правильно.

7. Любым символом отмечают все имеющиеся в таблице нетипичные сдвиги. В нашем случае – это три положительных сдвига.

8. Суммируют ранги нетипичных сдвигов. Это и будет искомая величина Т. В нашем случае эта сумма равна: Тэмп = 6,5 + 13,5 + 6,5 = 26,5.

По таблице определяют критические значения Т для n = 19. Подчеркнем, что в данном критерии, в отличие от критерия знаков, поиск критических величин в таблице 2 Приложения ведется по общему числу испытуемых.

Нужная нам строка таблицы Приложения выделена ниже в таблицу 6.6:

Таблица 6.6

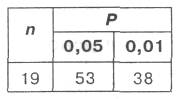
Поскольку в нашем случае основной, типичный сдвиг – отрицательный, то дополнительный, “нетипичный” сдвиг будет положительным и на уровне значимости в 5% сумма рангов таких сдвигов не должна превышать числа 53, а при уровне значимости в 1 % не должна превышать числа 38. Используем принятую форму записи, представим сказанное выше следующим образом:

Строим “ось значимости”:

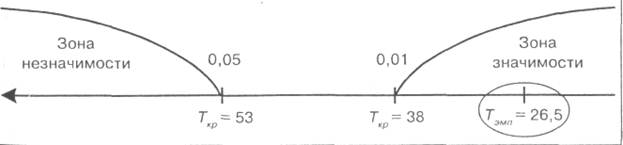
Анализ “оси значимости” показывает, что полученная величина Т эмп попадает в зону значимости. Можно утверждать, следовательно, что зафиксированные в эксперименте изменения неслучайны и значимы на 1 % уровне. Таким образом, применение коррекционных упражнений способствует повышению точности выполнения корректурной пробы.

Полученный результат может быть переформулирован в терминах нулевой и альтернативной гипотез: поскольку преобладание типичного отрицательного направления сдвига в данном конкретном эксперименте не является случайным, то должна быть принята гипотеза Н1, о наличии различий, а гипотеза Н0 отклонена.

Обращаем ваше внимание на то, что направление “оси значимости” в этом критерии, так же как и критерии знаков, имеет положение нуля справа, в отличие от традиционного – слева, и увеличение числового ряда идет в противоположную сторону.

Глава 7

Дата добавления: 2014-12-27