Сравнение двух экспериментальных распределений

На практике значительно чаще встречаются задачи, в которых необходимо сравнивать два и более эмпирических распределения между собой.

Исходные данные двух эмпирических распределений для сравнения между собой могут быть представлены разными способами. Наиболее простой из этих способов: так называемая «четырехпольная таблица». Она используется в тех случаях, когда в первой выборке имеются два значения (числа) и во второй выборке также два значения (числа). Критерий хи-квадрат позволяет также сравнивать между собой три, четыре и большее число эмпирических величин. Для расчетов во всех этих случаях используются различные модификации формулы (8.1), что позволяет существенно облегчить процесс вычисления.

Начнем изучение сравнения двух эмпирических распределений с самого простого случая – использования четырехпольной таблицы.

Задача 8.5. (Задача взята из учебного пособия «Психологическая диагностика» под ред. К.М. Гуревича и М.К. Акимовой. М. Изд-во УРАО, 1997 г.)

Одинаков ли уровень подготовленности учащихся в двух школах, если в первой школе из 100 человек поступили в вуз 82 человека и во второй школе из 87 человек поступили в вуз 44?

Решение. Условия задачи можно представить в виде четырехпольной таблицы 8.6 ячейки которой, обозначаются обычно как А, В, Си D:

Таблица 8.6

	1 школа	2 школа
Число поступивших в вуз	А 82	B 44
Число не поступивших в вуз	С 18	D 43
Сумма

Согласно данным, представленным в таблице 8.6, в нашем случае имеется четыре эмпирические частоты, это соответственно 82, 44, 18 и 43. Для того чтобы можно было использовать формулу (8.1), необходимо для каждой из этих эмпирических частот найти соответственные «теоретические» частоты. Здесь и далее, в других задачах этого раздела, «теоретические» частоты вычисляются на основе имеющихся эмпирических частот разными способами, в зависимости от типа задачи. Вычислим четыре теоретических частоты в нашем случае.

Из таблицы 8.6 следует, что 18 и 43 человека из первой и второй школ соответственно не поступили в вуз. Относительно этих величин подсчитывается величина Р. Это так называемая доля признака, или частота. В данном случае признаком явилось то, что выпускники не поступили в вуз. Величина Р подсчитывается по формуле (8.5) следующим образом:

Величина Р позволяет рассчитать «теоретические» частоты для третьей строчки таблицы 8.6, которые обозначим как f m1 и f m2

Эти частоты показывают, сколько учащихся из первой и второй школ не должны были поступить в вуз. Они подсчитывается следующим образом:

f m1 для первой школы = 0,33 • 100 = 33

f m2 для второй школы = 0,33 • 87 = 28,71

Иными словами, из первой школы не должны были поступить в вуз 33 человека, а из второй 28,71. (Для большей точности вычислений по методу «хи-квадрат» желательно не округлять результаты вычислений, а сохранять сотые и даже тысячные значения после запятой).

Исходя из вновь полученных «теоретических» частот – 33 и 28,71, мы можем произвести расчет того, сколько учащихся должны были бы теперь поступить в вуз из первой и второй школ. Обозначим эти частоты как f m3 для первой и f m4 для второй школ, получим соответственно:

f m3для первой школы 100 – 33 = 67

f m4 для второй школы 87 – 28,71 = 58,29

Перепишем полученные «теоретические» частоты в новую таблицу 8.7

Таблица 8.7

	1 школа	2 школа
Число учащихся, которые должны были бы поступить в вуз	А f m3 = 67	В f m4 = 58,29
Число учащихся, которые не должны были бы поступить в вуз	С f m1 = 33	Df m2 = 28,71
Сумма

Подчеркнем, что сумма по столбцам для вновь найденных «теоретических» частот, должна совпадать с исходной, т.е. 67 + 33 = 100 и 82 + 18 = 100, аналогично – 58,29 + 28,71 = 87 и 44 + 43 = 87. Подчеркнем также, что при расчетах «теоретических» частот им можно было бы дать и другое символическое обозначение, более привычное. Так, первую подсчитанную «теоретическую» частоту, представленную в ячейке С таблицы 8.7 можно было бы обозначить не как fт1 = 33, а как fт3= 33 и так далее. Это, однако, непринципиально, главное производить вычисления строго по алгоритму, в соответствии с формулой (8.1).

Теперь величина хи-квадрат эмпирическая подсчитывается по знакомой формуле (8.1). Для этого из величин, представленных в ячейках таблицы 8.6 вычитаются соответствующие величины, представленные в ячейках таблицы 8.7:

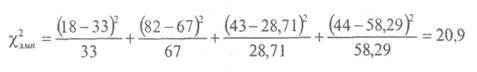
В данном случае число степеней свободы v = (k – 1) • (с – 1) подсчитывается как произведение числа столбцов минус 1 на число строк минус 1. Иными словами, v = (2 – 1) – (2 – 1) = 1, поскольку у нас 2 строки и два столбца. И в соответствии с таблицей 12 Приложения 1 находим:

Строим «ось значимости»:

Полученная величина «хи-квадрат» эмп попала в зону значимости. Иными словами, следует принять гипотезу Н1 о наличии различий между двумя эмпирическими распределениями. Таким образом, уровень подготовленности учащихся в двух школах оказался разным. На основе эмпирических данных мы можем теперь утверждать, что уровень подготовленности учащихся в первой школе существенно выше, чем во второй. Без использования критерия «хи-квадрат» такого вывода мы сделать бы не могли.

Для таблиц число степеней свободы определяется по формуле: v = (k – 1) • (с – 1), где k – число столбцов, с – число строк.

Глава 9

Дата добавления: 2014-12-27