Табличные интегралы. Вычисление интегралов

Табличные интегралы

Интегралы, которые применяются для интегрирования элементарных функций и их комбинаций, называются табличными интегралами. Ниже приводятся основные табличные интегралы.

1. 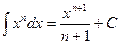, n Î R, n ¹ –1

2.

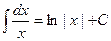
3.

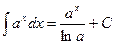
3а.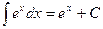

4.

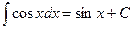
5.

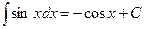
6.

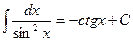
7.

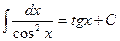
8.

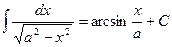
9.

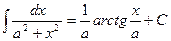
10.

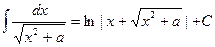
11.

§4.3 Непосредственное интегрирование, интегрирование подстановкой, интегрирование по частям

Непосредственное интегрирование

Интегрирование называется непосредственным, если при интегрировании применяются только свойства интегралов и табличные интегралы.

@ Задача 1. Интегрировать функцию

.

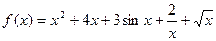Решение: Интеграл вычисляется непосредственно с помощью свойств неопределенных интегралов и табличных интегралов:

.

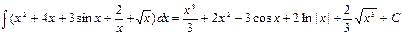Замечание: Нет нужды выписывать при промежуточных вычислениях для каждого интеграла свое постоянное слагаемое; достаточно приписать его по выполнения всех интегрирований.

Способ подстановки

Этот способ применяется, как правило, если подинтегральная функция сложная и нет возможности сразу брать интеграл с помощью табличных интегралов.

В подинтегральное выражение вместо x вводится вспомогательная переменная z, связанная с x некоторой зависимостью (как правило, аргумент подинтегральной сложной функции), после чего интеграл сводится к табличному интегралу.

@ Задача 2. Вычислить .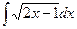

Решение: Производится замена переменных 2x – 1 = z, после чего 2x – 1 = z и dx = dz/2 подставляются в подинтегральное выражение, и интеграл сводится к табличному интегралу:

.

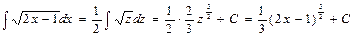@ Задача 3. Вычислить .

Решение: Производится замена переменных 1 + x² = z, после чего находим 2xdx = dz. После подстановки получим:

.

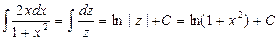@ Задача 4. Вычислить .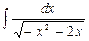

Решение: Под квадратным корнем, выделив полный квадрат, интеграл можно свести к табличному интегралу:

.

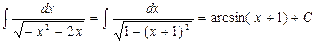Интегрирование по частям

Интегрированием по частям называется интегрирование по формуле:

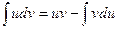, (1).

Этот способ интегрирования применяется в тех случаях, когда подинтегральная функция представляет собой произведение степенной и показательной функций, степенной и тригонометрической функций и т.д.

@ Задача 5. Вычислить .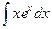

Решение: В подинтегральном выражении производятся замены x = u; e^xdx = dv, тогда v = e^x; du = dx. После этого применяется формула (1):

.

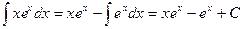@ Задача 6. Вычислить .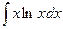

Решение: В подинтегральном выражении производятся замены lnx = u; xdx = dv, тогда 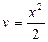; 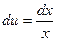. После этого применяется формула (1):

.

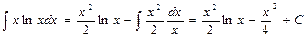@ Задача 7. Вычислить .

Решение: В подинтегральном выражении производятся замены x² = u; sinxdx = dv, тогда v = – cosx; du = 2xdx и формула (1) применяется дважды:

Интегралы от тригонометрических функций

@ Задача 8. Вычислить интеграл .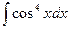

Решение: = = .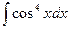

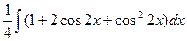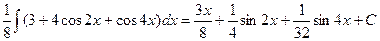Интегралы от дробно-рациональных выражений

@ Задача 9. Вычислить интеграл от дробно-рациональной функции: .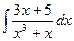

Решение: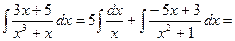

=

Если при интегрировании невозможно найти первообразную, или она не выражается элементарной функцией, то говорят, что интеграл «не берется».

Например, такими интегралами являются интеграл Пуассона, интегралы Френеля, интегральный синус и т.д.

Тесты по теме №4

1. Вычислить неопределенный интеграл .

£

£

£

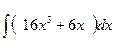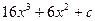
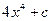
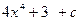
R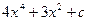

2. Интеграл 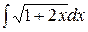равен…

£

£

£

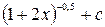
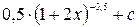
R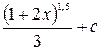

3. Интеграл 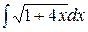равен…

£

£

£

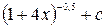
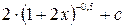
R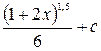

4.Интеграл 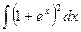равен...

R

£

£

£

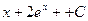
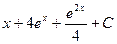
5.Множество первообразных функции имеет вид:

R

£

£

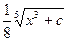
6.Множество первообразных функции f(x) = sin(5x+2) имеет вид...

£

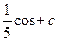
R

£

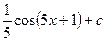
7.Множество первообразных функции f(x) = имеет вид:

R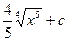

£

£

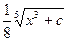
8. Найти неопределенный интеграл:

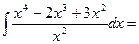
R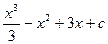

£

£

£

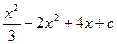
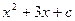
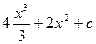
9. Найти неопределенный интеграл:

£

£

£

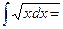
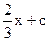
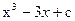
R

10. Найти неопределенный интеграл:

£

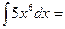
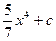
R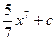

£

£

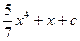
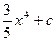
Дата добавления: 2014-12-27