Определенный интеграл и его свойства

Тема №5. Определенный интеграл

Определенный интеграл

Вычислим площадь криволинейной трапеции, ограниченной функцией y = f(x), линиями x = a, x = b и осью OX. Разделим отрезок [ a; b ] на n частей и вычислим сумму площадей полученных прямоугольников S y_iDx_i.

Предел суммы S y_iDx_i при Dx_i ® 0 обозначается как 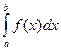и называется определенным интегралом f(x) от a до b.

Это есть геометрическое истолкование определенного интеграла.

Определенный интеграл с пределами интегрирования a и b вычисляется как разность первообразных в точках b и a (формула Ньютона-Лейбница): («эф с двойной подстановкой от a до b»).

þ Обозначения: a - нижний предел интегрирования, b - верхний предел интегрирования

Свойства определенных интегралов

1. Постоянный множитель можно вынести за знак интеграла: .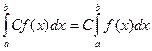

2. Интеграл суммы (разности) равен сумме (разности) интегралов: .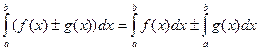

3. При равных пределах интегрирования интеграл равен нулю: .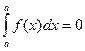

4. При перестановке пределов интегрирования интеграл меняет знак: .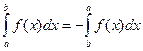

5. Интеграл можно представить в виде суммы двух интегралов 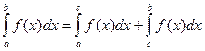, где с новый предел интегрирования, который может находиться как в интервале (a, b), так и вне этого интервала.

Механическое истолкование определенного интеграла

Если подынтегральной функцией является механическая скорость v (t), то определенный интеграл представляет собой пройденный телом путь 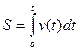, где t – время в пути и переменная интегрирования. Это есть механическое истолкование определенного интеграла.

Способ подстановки в определенных интегралах

Суть способа подстановки в замене переменного интегрирования x через другую переменную z:

,

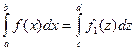где с и d – пределы интегрирования переменной z.

@ Задача 1. Вычислить .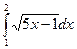

Решение: Производится замена переменных 5x – 1 = z; dx = dz/5; с = 4; d = 9:

.

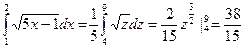@ Задача 2. Вычислить .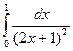

Решение: Производится замена переменных 2x + 1 = z; dx = dz/2; с = 1; d = 3:

.

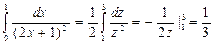Интегрирование по частям

Интегрированием по частям называется интегрирование по формуле:

.

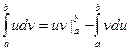@ Задача 3. Вычислить .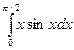

Решение: .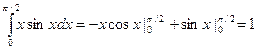

Несобственные интегралы

Определенный интеграл с одним или двумя бесконечными пределами интегрирования называется несобственным интегралом первого типа.

þ Обозначения: , , .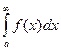

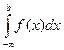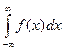@ Задача 4. Вычислить .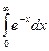

Решение: .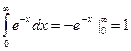

Известным примером несобственного интеграла является интеграл Эйлера-Пуассона: .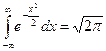

Определенный интеграл с функцией f(x), имеющий разрыв на отрезке [ a; b ], называется несобственным интегралом второго типа.

Пример: Подынтегральная функция интеграла 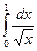в точке x = 0 имеет разрыв.

Приближенное вычисление

На практике часто встречаются интегралы, которые не выражаются через элементарные функции. В этом случае интегралы можно взять приближенными методами: по формулам прямоугольников, трапеций и Симпсона.

По формуле трапеций интеграл вычисляется как

,

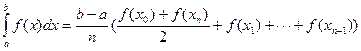где 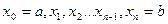- точки отрезка [ a; b ].

Предельная погрешность формулы трапеций составляет 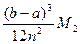, где M ₂– наибольшее значение | f²(x)| в промежутке [ a; b ].

Пример. .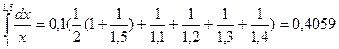

По формуле Симпсона (параболических трапеций) интеграл вычисляется как

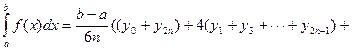
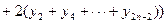
Предельная погрешность формулы Симпсона составляет 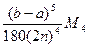, где M ₄– наибольшее значение | f ^IV (x)| в промежутке [ a; b ].

Дата добавления: 2014-12-27