Ряд, членами которого являются степенные функции, называется степенной

СТЕПЕННЫЕ РЯДЫ

,

где числа а₀, а₁, ¼ а_п называются коэффициентами ряда.

При x = x₀ степенной ряд превращается в числовой ряд. Если полученный числовой ряд сходится, то точка x₀ называется точкой сходимости ряда, если ряд расходится – точкой расходимости.

Совокупность числовых значений x, при которых степенной ряд сходится, называется его областью сходимости.

Теорема Абеля

Если степенной ряд сходится при x = x₀ ¹ 0, то он абсолютно сходится при всех значениях |x| < |x₀|.

Следствие: Если ряд расходится при x = x₁, тоон расходится и при всех | x| > |x₁ |.

Из теоремы Абеля следует, что если x₀ ¹ 0 есть точка сходимости степенного ряда, то интервал (– |x₀ |; |x₀ |) весь состоит из точек сходимости данного ряда; при всех значениях x вне этого интервала степенной ряд расходится.

Интервал (– |x₀ |; |x₀ |) называется интервалом сходимости степенного ряда. Число R = |x₀ | называется радиусом сходимости степенного ряда, т.е. при всех x, для которых | x| < R, ряд абсолютно сходится, а при | x| > R ряд расходится.

В частности, когда степенной ряд сходится лишь в одной точке x₀ = 0, то считается, что R = 0. Если же ряд сходится при всех значениях x Î R (т.е. во всех точках числовой оси), то считается, что R = ∞.

Отметим, что на концах интервала сходимости (т.е. при x = R и при x = – R) сходимость ряда проверяется в каждом конкретном случае отдельно.

Согласно признаку Даламбера радиус сходимости степенного ряда определяется как , а согласно признаку Коши - R = 1 / .

@ Задача 1. Найти радиус сходимости степенного ряда .

Решение: Радиус сходимости можно найти по формуле Даламбера

= .

Следовательно, степенной ряд абсолютно сходится на всей числовой оси.

@ Задача 2. Найти радиус сходимости степенного ряда .

Решение: Радиус сходимости находим по формуле Коши

R = 1 / = .

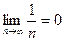Следовательно, степенной ряд сходится лишь в одной точке x₀ = 0.

Свойства степенных рядов

1. Сумма S(x) степенного ряда является непрерывной функцией в интервале сходимости (– R; R).

2. Степенные ряды 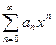и , имеющие радиусы сходимости соответственно R₁ и R₂, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел R₁ и R₂.

3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать:

Полученный степенной ряд имеет тот же радиус сходимости, что и исходный степенной ряд.

4. Степенной ряд можно почленно интегрировать на каждом отрезке внутри интервала сходимости:

Полученный степенной ряд имеет тот же радиус сходимости, что и исходный степенной ряд.

Ряд Тейлора

Функцию f(x) можно представить в виде бесконечного степенного ряда, который называется рядом Тейлора:

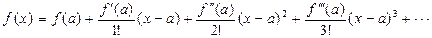
Частный случай этого ряда при a = 0 называется рядом Маклорена:

! Примеры: ,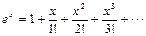

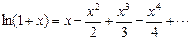
Значение функции в точке x = b можно приближенно найти с помощью ограниченного ряда Тейлора (с помощью первых n членов) (формула Тейлора):

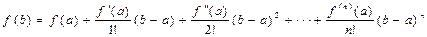(1),

допустив при этом ошибку (остаточный член Лагранжа):

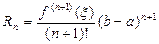, (2)

где x - некоторое число, лежащее между a и b.

Коши доказал, что f(x) разлагается в ряд Тейлора, если .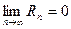

@ Задача 3. Найти формулы для вычисления чисел e, 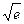и функции .

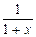Решение: e и 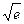находятся с помощью формулы (1) и остаточного члена (2):

, ,

, .

Функция находится с помощью выражения для f(x) (формула (1), только вместо b нужно подставить x) и остаточного члена (2):

, .

Тестовые задания по теме №3

1. Решением неравенства f(x) f(2) с монотонно убывающей на R функцией f служит множество …

£

R

£

2. Область значений функции y = -2cos2x + 1 есть отрезок …

£ [-2, 2]

£ [-2, 0]

£ [0, 2]

R [-1, 1]

3. Из нижеперечисленных функций выберите ту, которая не является первообразной к f(x) = 3x …

£ F(x) = x3

£ F(x) = x3+ 1

£ F(x) = (x + 1)3 - 3x -3x

R F(x) = (x + 1)3 + 2

4. Из нижеперечисленных функций выберите ту, которая не является первообразной к f(x) = 3x …

£ F(x) = x³+ 1

£ F(x) = (x + 1)³ – 3x -3x

R F(x) = (x + 1)³ + 2

£ F(x) = x³

5. Для функции точка x=0 является точкой …

£ разрыва

£ перегиба

£ минимума

R максимума

6. Для функции обратной является функция…

£

R

£

£

7. Для функции точка является точкой…

£ непрерывности

£ разрыва II рода

£ точкой экстремума

R устранимого разрыва

8. Предел равен…

£

£ 1

£

R 2

9. Для функции 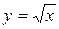обратной является функция…

£

R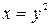

£

£

10. Найти производную функцию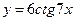

£

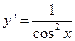
R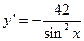

£

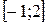11. Функция отображает отрезок на отрезок…

£

R

£

£

12. Найти частное производное f¢_x функции f(x, y) = x ² y – 2xy в точке (2; – 1).

£ 3

R 0

£ – 2

£ 1

13. Найти производную функции:

£ 25х+18

R

£ 3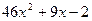

£

14. Для функции 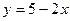обратной является функция…

£

R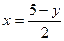

£

£

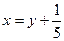
15. Найти производную функции:

£ 25х+18

R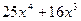

£

£

16. Найти производную функции:

R

£

£

£

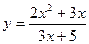
17.Найти производную функции:

£

£

£

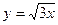
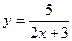
R

18. Найти частное значение функции:

в точке В(2, -4)

£

£

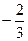
R

£

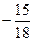
19. Предел 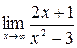равен…

£

£ 1

£

R 0

20. Общее решение линейного однородного дифференциального уравнения имеет вид …

£

£

R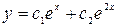

£

21. Общее решение линейного однородного дифференциального уравнения имеет вид …

£

£

R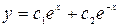

£

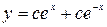
22. Общим решением дифференциального уравнения является …

£

£

R

£

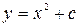
23. Общим решением дифференциального уравнения является …

£

£

R

£

24. Функция 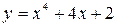на всей числовой оси…

£ монотонно убывает

R выпукла вниз

£ выпукла вверх

£ монотонно возрастает

25. Функция 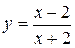бесконечно малая в точке…

R

£

£

£

26. Частное решение дифференциального уравнения при начальном условии имеет вид…

£

£

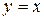
R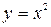

£

27. Предел 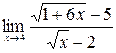равен…

£

£ 2

R 12/5

£ 3/20

Дата добавления: 2014-12-27