Дифференциальные уравнения первого порядка

Уравнение, содержащее независимую переменную x, функцию y и ее производные, называется дифференциальным уравнением: F(x; y; y ′; y ′′ ¼ y⁽ⁿ⁾) = 0.

Наивысшим порядком производной определяется порядок дифференциального уравнения.

Решением дифференциального уравнения называется функция, которая при подстановке ее в уравнение обращает его в тождество. Решение называется также интегралом.

Процесс отыскания решения дифференциального уравнения называется его интегрированием, а график решения – интегральной кривой.

Классическим примером дифференциального уравнения является уравнение движения материальной точки в классической механике: mx² = F(t), где m – масса материальной точки, x² - производная второго порядка координаты точки по времени, F(t) – сила, действующая на материальную точку.

Дифференциальное уравнение первого порядка

Дифференциальное уравнение первого порядка – это уравнение, связывающее независимую переменную x, искомую функцию y и ее первую производную y ′ :

F(x; y; y ′ ) = 0. (1)

Пример: xy′ + ylny′ = 0.

Если уравнение (1) разрешается относительно y ′, то его записывают в виде y′ = f(x; y) (2) и оно называется дифференциальным уравнением первого порядка, разрешенным относительно производной y ′.

Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме: P(x; y)dx + Q(x; y)dy = 0. (3)

Уравнение вида (2) сводится к уравнению дифференциальной формы (3) следующим образом:

, dy = f(x; y)dx, f(x; y)dx – dy = 0.

Обратный переход из (3) в (2) производится делением уравнения (3) на dx: .

Общим решением дифференциального уравнения первого порядка называется функция y = φ(x; c), которая является решением уравнения при каждом фиксированном значении постоянной с.

Частным решением дифференциального уравнения первого порядка называется функция y = φ(x; c₀), удовлетворяющая начальному условию 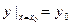. (4)

В теории дифференциальных уравнений основной задачей является вопрос о существовании и единственности решения. Задача нахождения частного решения дифференциального уравнения называется задачей Коши.

Теорема существования и единственности решения задачи Коши: Если в уравнении (2) функция f(x; y) и ее частная производная f¢_y(x, y) непрерывны в некоторой области D, содержащей точку (x₀, y₀), то существует единственное решение y = φ(x; c₀) этого уравнения, удовлетворяющее начальному условию (4).

Пример: Решениями дифференциального уравнения y′ = 3x² являются y = x³, y = x³ + 1, y = x³ + 3и т.д. Другими словами, общее решение дифференциального уравнения представляет собой семейство интегральных кривых y = x³ + c. Из этого множества функций есть только одна, график которой проходит через заданную точку, т.е. удовлетворяет начальному условию (4). В частности, при решение дифференциального уравнения имеет вид y = x ³ + 1.

Из дифференциального уравнения (2) следует, что угловой коэффициент касательной к интегральной кривой в каждой ее точке равен правой части этого уравнения, т.е. функции f(x; y). Если построить семейство функций f(x; y) = c (изоклины), то для каждого c во всех точках функции f(x; y) = c производная y ′ постоянная, т.е. угловые коэффициенты одинаковые. Если в каждой точке построить эти касательные, то получим поле направлений данного уравнения. В этом и заключается геометрический смысл дифференциального уравнения первого порядка. Задача интегрирования уравнения (2) геометрически формулируется так: найти линии, у которых направление касательной всюду совпадает с направлением поля.

Дифференциальное уравнение с разделяющимися переменными

Общий вид уравнения с разделяющимися переменными имеет вид:

P₁(x)Q₁(y)dx + P₂(x)Q₂(y)dy =0.

Дифференциальное уравнение решается методом разделения переменных.

После почленного деления уравнения на Q₁(y)P₂(x) ¹ 0 получается дифференциальное уравнение с разделенными переменными, т.е. появляется возможность его интегрирования. После интегрирования получаем общее решение дифференциального уравнения:

,

где с – произвольная постоянная.

При проведении почленного деления дифференциального уравнения на Q₁(y)P₂(x) могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение Q₁(y)P₂(x) = 0 и установить решения дифференциального уравнения, которые не могут быть получены из общего уравнения. Они называются особыми решениями.

Уравнение y′ = f(ax + by + c), где а, b, с – действительные числа, сводится к уравнению с разделяющимися переменными после замены переменных ax + by + c = u. После дифференцирования a + by¢ = u¢, a + bf(u) = u¢, получим уравнение .

@ Задача 1. Найти общее решение дифференциального уравнения:

2yxdx – ( 1 + x ² )dy = 0.

Решение: После почленного деления уравнения на y(1 + x ² ) получаем: , которое легко интегрируется: ln/y/ – ln( 1 + x ² ) = ln/c/. Общее решение дифференциального уравнения имеет вид: y = с( 1 + x ² ).

Уравнение y( 1 + x ² ) = 0 позволяет найти особое решение дифференциального уравнения: y = 0.

@ Задача 2. Найти частное решение дифференциального уравнения:

при y (1) = 1.

Решение: После почленного деления уравнения на y получаем: . Остается только интегрировать уравнение: ln/y/ + ln/x/ = ln/c/. Общее решение дифференциального уравнения имеет вид: , а частное решение равно .

Однородное дифференциальное уравнение

Дифференциальное уравнение (2) называется однородным, если функция f(x; y) является однородной функцией нулевого порядка.

Функция является однородной функцией нулевого порядка, если f(lx, ly) = f(x, y) = y(y/x). Однородное дифференциальное уравнение преобразуется в уравнение с разделяющимися переменными при помощи замены y/x = u, откуда y′ = xu′ + u. Подставляя эти выражения в (2), получим xu′ + u = y(u), т.е. xu′ = y(u) – u. Таким образом, мы получили дифференциальное уравнение с разделяющими переменными.

Если уравнение имеет дифференциальную форму (3), то оно называется однородной, если P(x; y) и Q(x; y) являются однородными функциями одинакового порядка: P(lx, ly) = lⁿP(x, y), Q(lx, ly) = lⁿQ(x, y).

И в этом случае однородное уравнение преобразуется в уравнение с разделяющимися переменными при помощи замены переменной y/x = u, откуда dy = udx + xdu.

Уравнение y′ = f((ax + by + c)/(dx + ey + f)), где а, b, с, d, e, f – действительные числа, сводится к уравнению с разделяющимися переменными после замены переменных x = u + α и y = v + β, где α и β - числа. Числа α и β находятся из уравнений a α + b β + c = 0, d α + e β + f = 0, которые получаются из следующих соотношений: ax + a α + by + b β + c = ax + by, dx + d α + ey + e β + f = dx + ey.

@ Задача 3. Найти общее решение дифференциального уравнения (x ² – y ² )dx + 2xydy = 0.

Решение: После замены переменной y/x = u получим уравнение x ² ( 1 + u ² )dx + 2x ³ udu = 0. После почленного деления уравнения на x³( 1 + u ² ) получаем: , которое легко интегрируется: ln/x/ + ln( 1 + u ² ) = ln/c/. Общее решение дифференциального уравнения имеет вид: x ² + y ² = cx.

Линейное дифференциальное уравнение. Дифференциальное уравнение Бернулли

Дифференциальное уравнение первого порядка называется линейным, если его можно записать в виде y′ + p(x)y = g(x) (5), где p(x) и g(x) – заданные функции.

Особенность линейного дифференциального уравнения в том, что функция y и ее производная y′ входят в уравнение в первой степени, не перемножаясь между собой.

Линейное дифференциальное уравнение первого порядка решается методом Лагранжа (методом вариации произвольной постоянной). Рассматривается линейное однородное дифференциальное уравнение без правой части y′ + p(x)y = 0, решение которого имеет вид 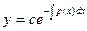. После этого постоянная с заменяется функцией c(x) и, решение однородного уравнения подставляя в неоднородное уравнение (5), получается уравнение для функции c(x):

,

.

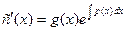В итоге, общее решение уравнения (5) имеет вид

.

@ Задача 4. Найти общее решение дифференциального уравнения: y′ + 2xy = 2x.

Решение: Подставим p(x) = 2x и g(x) = 2x в общее решение линейного дифференциального уравнения:

.

Уравнение вида 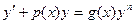при n ¹ 0; 1 называется уравнением Бернулли.

Уравнение Бернулли сводится к линейному уравнению z′ + (1 – n)p(x)z = (1 – n)g(x) заменой переменного y^1-n = z. На самом деле z′ = (1 – n)y^-ny′ = – (1 – n)y^-np(x)y + (1 – n)g(x), z′ + (1 – n)p(x)z = (1 – n)g(x).

Дифференциальное уравнение в полных дифференциалах

Уравнение P(x; y)dx + Q(x; y)dy = 0 называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции u(x; y), что имеет место при выполнении условия 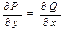. (6)

Если левая часть дифференциального уравнения представить в виде полного дифференциала, то получим , . Интегрируем первое уравнение: . Применяя второе уравнения, получим уравнение для неизвестной j(y): 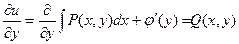, откуда можно найти j(y):

.

В итоге общее решение дифференциального уравнения в полных дифференциалах имеет вид

.

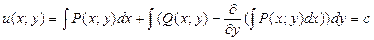@ Задача 5. Найти общее решение дифференциального уравнения (2xy – 5)dx + (3y ² + x ² )dy = 0.

Решение: Проверим выполнение условия (6): 2x = 2x. Подставим P(x; y) = 2xy – 5 и Q(x; y) = 3y ² + x ² в общее решение дифференциального уравнения в полных дифференциалах: =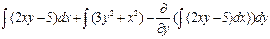

= , x ² y – 5x + y ³ = c.

Правило: Чтобы найти общее решение дифференциального уравнения, интегрируем 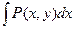при постоянном значении y, интегрируем при постоянном x и объединяем эти выражения, сохраняя повторяющие члены только один раз.

Дата добавления: 2014-12-27