Предел последовательности и его свойства. Функция называется целочисленной или последовательностью, если область определения функции представляет собой множество натуральных чисел

Функция называется целочисленной или последовательностью, если область определения функции представляет собой множество натуральных чисел.

þ Обозначения: Последовательности обозначаются как { a_n }, { y_n }, члены последовательности как – a_n, y_n.

Число b называется пределом последовательности { y_n }, если по мере возрастания n член y_n неограниченно приближается к значению b:

.

Символ lim от латинского слово «limes» - предел; символ n ® ¥ подчеркивает, что n неограниченно возрастает («стремится к бесконечности»).

! Примеры: Члены последовательности 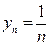по мере возрастания n стремятся к нулю: y₁ = 1; y₂ = 0,5; y₃ = 0,33¼; y₄ = 0,25; ¼; y₁₀₀ = 0,01; ¼; y₁₀₀₀ = 0,001; ¼ Следовательно, пределом последовательности является число 0:

. (1)

! Пример: Члены последовательности 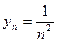по мере возрастания n стремятся к нулю, поэтому . (2)

! Пример: Предел постоянной величины c равен самой постоянной величине c (3).

Более строгое определение предела следующее.

Число b называется пределом последовательности {y_n}, если абсолютная величина разности y_n – b, начиная с некоторого номера N, остается меньшей любого заранее данного положительного числа e: |y_n – b| < e при n ³ N (N зависит от величины e).

Последовательность, имеющая предел, называется сходящейся, в противном случае, она расходящаяся.

Свойства пределов

1. Постоянный множитель можно вынести за знак предела: .

2. Предел суммы (разности) равен сумме (разности) пределов: .

3. Предел произведения равен произведению пределов: .

4. Предел отношения равен отношению пределов: , если .

Эти свойства справедливы не только для последовательностей, но и для функций y(x).

@ Задача 1. Найти предел последовательности .

Решение: Предел последовательности находится, применяя второе свойство пределов и частные пределы (2) и (3):

.

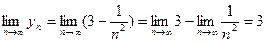Бесконечно большая величина

Бесконечно большой величиной называется величина, абсолютное значение которой неограниченно возрастает.

! Примеры: Величины n, n², n³ являются бесконечно большими величинами, при n ® ¥; - при x ® 0, tgx - при x ® p/2: ; ; .

Функция f(x) есть бесконечно большая величина при x ® a, если абсолютное значение f(x) остается большим любого заранее данного положительного числа N, всякий раз как абсолютное значение разности x – a меньше некоторого положительного числа d (зависящего от N).

Бесконечно большая величина не имеет предела по определению, ибо никак нельзя сказать, что «разность между f(x) и ¥ остается меньшей заранее данного положительного числа». Таким образом, введение беcконечного предела расширяет понятие предела. В отличие от бесконечного предела предел, определенный ранее, называется конечным.

Функция y_n называется бесконечно большой величиной высшего порядка по сравнению с z_n, если предел их отношения ¥.

Из этого свойства вытекает следующее правило. При вычислении пределов, содержащих сумму y_n и z_n, где функция y_n является бесконечно большой величиной высшего порядка по сравнению с z_n, функцию z_n можно пренебречь по сравнению с y_n.

@ Задача 2. Найти предел последовательности .

Решение: Если непосредственной подстановкой n попытаться найти предел последовательности, то мы получим неопределенность вида . Здесь термин неопределенность применяется в том смысле, что сразу невозможно сказать к какому пределу стремится последовательность. Определение предела называется раскрытием неопределенности. В данном случае неопределенность можно раскрыть с учетом вышесказанного. Так как n ² является бесконечно большой величиной высшего порядка по сравнению с n и 2, то последние члены в числителе можно пренебречь. То же самое относится и к знаменателю. Итак

.

Предел функции

Число b называется пределом функции f(x) при x, стремящийся к a (x ® a), если, по мере приближения x к a, значение функции неограниченно приближается (стремится) к b:

.

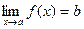! Пример: Функция f(x) = 2x + 3 при x, стремящийся к a, f(x) стремится к 3, т.е. .

Более строгое определение предела следующее.

Число b называется пределом функции f(x) при x ® a, если абсолютное значение разности f(x) – b остается меньшим любого заранее данного положительного числа e всякий раз, как абсолютное значение разности x – a меньше некоторого положительного числа d (зависящего от e).

Предполагается, что функция f(x) определена внутри некоторого промежутка, содержащего точку x = a (во всех точках справа и слева от a), в самой же точке x = a f(x) либо определена, либо нет.

Если какая-либо функция не определена в точке x = a, но обладает пределом при x ® a, то разыскивание этого предела называется раскрытием неопределенности. Раскрытие неопределенности вида называют разыскивание предела отношения функций f(x) и g(x), бесконечно малых величины при x ® a.

@ Задача 3. Найти предел функции при .

Решение: Мы имеем дело с неопределенностью вида . Разложив квадратичные трехчлены числителя и знаменателя в множители, и применив свойства пределов, находим предел функции f(x):

.

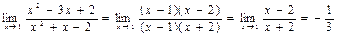@ Задача 4. Найти предел функции 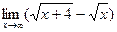при x ® ¥.

Решение: Мы имеем дело с неопределенностью типа ¥ – ¥.

.

Замечательные пределы

Первым замечательным пределом называется предел

.

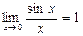Вторым замечательным пределом называется предел

или .

@ Задача 5. Найти предел функции 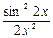при x ® 0.

Решение: Предел находится применением первого замечательного предела и свойств пределов:

.

@ Задача 6. Найти предел функции при x ® 0.

Решение: Предел находится применением второго замечательного предела:

,

где z = 2x.

Множество применений имеют также следующие пределы

; ; .

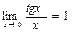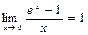Бесконечно малая величина

Бесконечно малой величиной называется величина, предел которой равен нулю.

! Примеры: Величины x, x², x³, sinx, 1 – cosx, tgx являются бесконечно малыми величинами, при x ® 0; величины , являются бесконечно малыми величинами, при n ® ¥: ; ; ; .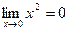

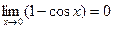Бесконечно малые величины обозначаются буквами a, b и т.д.

Дата добавления: 2014-12-27