Предел и непрерывность функции

Две бесконечно малые величины называются эквивалентными, если предел их отношения равен единице.

! Пример: x, sinx и tgx являются эквивалентными x ® 0.

Из свойства эквивалентности вытекает следующее правило при раскрытии неопределенностей. Под пределом одну эквивалентную величину можно заменить другой эквивалентной величиной.

Например, sinx и tgx можно заменить на x, sin2x и tg2x - на 2x, ln(1 + 3x) - на 3x и т.д x ® 0.

Если отношение a/b двух бесконечно малых величин само бесконечно мало, то называется величиной высшего порядка малости относительно b.

! Пример: x² является бесконечно малой высшего порядка малости относительно бесконечно малой x при x ® 0.

Если y – бесконечно большая величина, то – бесконечно малая и наоборот.

@ Задача 7. Найти предел функции при x ® 0.

Решение: Предел находится применением свойств бесконечно малых величин:

.

Функция y = f(x) называется непрерывной в точке x = a, если соблюдаются следующие два условия:

1. при x = a функция имеет определенное значение b,

2. при x ® a функция имеет предел, равный b.

При нарушении хотя бы одного из этих условий функция называется разрывной в точке x = a.

Точка x = a называется точкой разрыва первого рода функции y = f(x), если в этой точке существуют конечные пределы функции слева (b ₁) и справа (b ₂) (односторонние пределы). Величину | b ₁ – b ₂| называют скачком функции.

Разрывная функция с точкой устранимого разрыва может стать непрерывной функцией, путем добавления значения f(x) = b в точке разрыва x = a. В приведенном примере – это значение f (0) = 1.

При b ₁ ≠ b ₂, точка x = a называется точкой конечного разрыва

Пример: , | b ₁ – b ₂| = 1.

При b ₁ = b ₂, точка x = a называется точкой устранимого разрыва

Пример: 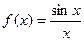, | b ₁ – b ₂| = |1 – 1| = 0.

Точка разрыва называется точкой разрыва второго рода функции y = f(x), если, по крайней мере, один из односторонних пределов (слева или справа) не существует или равен бесконечности.

@ Задача 1. Найти точку разрыва функции . Выяснить род разрыва.

Решение: x = 3 является точкой разрыва функции (функция не определена в этой точке). Левосторонний предел равен b ₁ = – 1, а правосторонний предел - b ₂ = 1, т.е. это означает, что мы имеем дело с точкой разрыва первого рода. Скачок равен | b ₁ – b ₂| = 2.

Учитывая вышесказанное, можно дать следующее определение. Функция непрерывна в точке x = a, если она определена в этой точке и выполняется условие D y ® 0 приD x ® 0, т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Функция y = cosx непрерывна в произвольной точке x, т.к. D cosx ® 0 приD x ® 0.

Функция называется непрерывной на замкнутом промежутке, если она непрерывна в каждой точке этого промежутка, включая оба конца.

Дата добавления: 2014-12-27