Линейные дифференциальные уравнения с постоянными коэффициентами

Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Линейное однородное дифференциальное уравнение второго порядка c постоянными коэффициентами – это уравнение y′′ + py′ + qy = 0 (7), где p и q – постоянные величины.

Общее решение дифференциального уравнения второго порядка имеет вид y = φ(x; c₁, c₂), где c₁, c₂ - некие постоянные величины.

Частное решение y = φ(x; c₁₀, c₂₀) получается из общего решения при выполнении начальных условий , .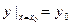

Общее решение уравнения (7) зависит от решений характеристического уравнения

k² + pk + q = 0.

Характеристическое уравнение получается из дифференциального уравнения (7) подстановкой функции .

1) Если корни k₁ и k₂ характеристического уравнения действительные и различные, то

.

2) Если корни k₁ и k₂ характеристического уравнения действительные и равные, то

.

3) Если корни k₁ и k₂ характеристического уравнения комплексные (k₁ = α + β i, k₂ = α – β i), то

.

@ Задача 1. Найти общее решение дифференциального уравнения: y′′ – 2y′ + y = 0.

Решение: Корни k₁ и k₂ характеристического уравнения k ² – 2k + 1 = 0 действительные и равны 1. Общее решение дифференциального уравнения имеет вид:

.

Линейное однородное дифференциальное уравнение n -го порядка с постоянными коэффициентами

Линейное однородное дифференциальное уравнение n -го порядка с постоянными коэффициентами – это уравнение 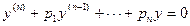, где p₁, p₂, …, p_n – постоянные величины.

1) Если все корни характеристического уравнения действительные и различные, то общее решение имеет вид

.

2) Если все корни характеристического уравнения действительные, но не все различные (с кратностью m), то общее решение содержит частные решения , , … .

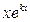3) Если какая-либо пара сопряженных комплексных корней имеет кратность m, то решение содержит частные решения cosbx, x cosbx, …, cosbx, sinbx, x sinbx, …, sinbx.

@ Задача 2. Найти общее решение дифференциального уравнения: .

Решение: Корни характеристического уравнения 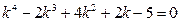равны – 1; 1; 1 + 2i и 1 – 2i. Общее решение дифференциального уравнения имеет вид:

.

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

y′′ + py′ + qy = f(x),

где p и q – постоянные коэффициенты, f(x) - правая часть уравнения, имеющая специальный вид.

Общее решение дифференциального уравнения представляет собой сумму общего решения y _общсоответствующего однородного уравнения и частного решения y _чнеоднородного уравнения.

Рассмотрим случай, когда f(x) имеет специальный вид f(x) = P_n(x) , где P_n(x) – многочлен степени n, a – действительное число. В этом случае частное решение неоднородного дифференциального уравнения ищется как

y _ч = x^rQ_n(x) ,

где r – число равное кратности a как корня характеристического уравнения k ² + pk + q = 0, Q_n(x) – многочлен степени n с неопределенными коэффициентами, которые нужно найти.

@ Задача 3. Найти общее решение дифференциального уравнения: .

Решение: Сначала находим общее решение однородного дифференциального уравнения. Характеристическое уравнение k² + 1 = 0 имеет корни i и – i. Общее решение однородного дифференциального уравнения имеет вид y_общ = c₁cosx + c₂sinx. Корни характеристического уравнения не совпадает с a = 1, поэтому r = 0. Частное решение неоднородного дифференциального уравнения ищется в виде y_ч = (Ax + B) . Для нахождения A и B это решение подставляется в неоднородное дифференциальное уравнение. Ax + 2A + B + Ax + B = 4x, откуда A = 2, B = – 2. Частное решение имеет вид y_ч = 2(x – 1)e^x. Общее решение неоднородного дифференциального уравнения равно

y = c₁cosx + c₂sinx + 2(x – 1) e^x.

Рассмотрим случай, когда f(x) = (P_n(x)cos β x + Q_m(x)sin β x), где P_n(x) и Q_m(x) – многочлены степени n и m, α и β - действительные числа. В этом случае частное решение неоднородного дифференциального уравнения ищется в виде

y _ч = x^r (M(x)cos β x + N(x)sin β x),

где M(x) и N(x) многочлены степени max(m, n).

§3.9. Числовые ряды

Числовые ряды

Числовым рядом называется бесконечная сумма чисел (1),

где - общий член ряда.

Конечная сумма чисел называется частичной суммой ряда.

Если S _n стремится к конечному пределу S, то говорят, что ряд сходится, а предел называется суммой ряда. Если предел ряда не существует или , то говорят, что ряд расходится.

! Пример: Числовой ряд сходится и сумма равна S = 1. Ряд с a_n = n расходится. Ряд с a_n = (– 1)ⁿ тоже расходится.

Свойства рядов

1. Если ряд (1) сходится и его сумма равна S, то ряд также сходится и его сумма равна cS.

2. Если ряд (1) и ряд сходятся, то сходятся также их сумма и разность.

3. Если к ряду (1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1) сходятся или расходятся одновременно.

Ряд геометрической прогрессии

Числовой ряд называется суммой геометрической прогрессии, если 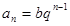(q – знаменатель прогрессии). Ряд геометрической прогрессии при q < 1 сходится, а при q > 1 расходится. Сумма геометрической прогрессии при q < 1 равна S = b/(1 – q). Это известная формула бесконечно убывающей геометрической прогрессии.

@ Задача 1. Найти сумму 1 + 1/3 + 1/9 + 1/27 + ···

Решение: Данный числовой ряд - это сумма бесконечно убывающей геометрической прогрессии с b = 1 и q = 1/3. Следовательно, сумма ряда равна S = 1/(1 – 1/3) = 1,5.

Необходимый признак сходимости числового ряда

Необходимый признак сходимости числового ряда определяется теоремой.

Теорема. Если ряд (1) сходится, то его общий член a_n стремится к нулю: (2).

Теорема дает необходимое условие сходимости ряда, но не достаточное, т.е. из условия (2) не следует, что ряд сходится.

В частности, гармонический ряд 1 + 1/2 + 1/3 + 1/4 + ··· расходится, хотя для него выполняется условие (2).

Ряд называется положительным, если все члены ряда положительные.

Достаточными признаками сходимости положительного числового ряда являются признак сравнения рядов, признак Даламбера, признак Коши и интегральный признак Коши.

Признак сравнения рядов

Сходимость такого ряда устанавливается путем сравнения его с другим (эталонным) рядом.

Если ряд , общие члены которого 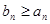, сходится, то сходится также ряд (1).

Если ряд , общие члены которого , расходится, то расходится также ряд (1).

@ Задача 2. Исследовать на сходимость числовой ряд .

Решение: По признаку сравнения рядов, так как ряд сходится, а также выполняется условие 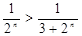, следовательно, наш ряд тоже сходится.

@ Задача 3. Исследовать на сходимость числовой ряд .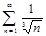

Решение: Согласно признаку сравнения т.к. , и гармонический ряд расходится, то приведенный ряд также расходится.

Признак Даламбера

Ряд сходится, если .

Если предел больше 1, то ряд расходится. Если предел равен 1, то ряд может быть как сходящимся, так и расходящимся. Признак Даламбера целесообразно применить, когда общий член ряда содержит выражение вида n! или .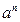

@ Задача 3. Исследовать на сходимость ряд .

Решение: По признаку Даламбера , т.е. ряд сходится.

Признак Коши

Ряд сходится, если .

Если предел больше 1, то ряд расходится. Если предел равен 1, то ряд может быть как сходящимся, так и расходящимся. Признак Коши целесообразно применить, когда общий член ряда содержит выражение вида .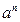

@ Задача 4. Исследовать на сходимость ряд .

Решение: По признаку Коши 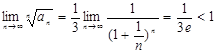, т.е. ряд сходится.

Интегральный признак Коши

Теорема: Если каждый член положительного ряда меньше предшествующего, то: а) если предел конечный, то ряд (1) сходится, б) если предел бесконечный, то ряд (1) расходится.

@ Задача 5. Исследовать на сходимость гармонический ряд .

Решение: Из интегрального признака Коши следует, что ряд расходится.

Ряд называется знакопеременным, если его члены поочередно положительны и отрицательны. Достаточным признаком сходимости знакопеременного числового ряда являются признак Лейбница.

Признак Лейбница

Знакопеременный ряд сходится, если его члены стремятся к нулю, все время убывая по абсолютному значению.

! Пример: Знакопеременный ряд 1 – 1/2 + 1/3 – 1/4 + ··· сходится согласно признаку Лейбница.

Знакопеременный ряд называется абсолютно сходящимся, если сходится положительный ряд, составленный из абсолютных значений членов данного ряда.

! Пример: Знакопеременный ряд 1 – 1/4 + 1/9 – 1/16 + ··· является абсолютно сходящимся.

Знакопеременный рядможет сходиться и тогда, когда ряд, составленный из абсолютных значений его членов, расходится.

Знакопеременный ряд называется условно сходящимся, если он сходится, но ряд, составленный из абсолютных значений его членов, расходится.

! Пример: Знакопеременный ряд 1 – 1/2 + 1/3 – 1/4 + ··· является условно сходящимся.

Дата добавления: 2014-12-27