Марковские процессы. Задачи анализа замкнутых и разомкнутых систем массового обслуживания

Нередко возникает необходимость в решении вероятностных задач, связанных с работой систем массового обслуживания (СМО), примерами которых могут служить билетные кассы, ремонтные мастерские, торговые, транспортные, энергетические системы, системы связи и др. Общность таких систем выявляется в единстве математических методов и моделей, применяемых при исследовании их деятельности.

На вход в СМО поступает поток требований на обслуживание. Например, клиенты или пациенты, поломки в оборудовании, телефонные вызовы. Требования поступают нерегулярно, в случайные моменты времени. Случайный характер носит и продолжительность обслуживания. Это создает нерегулярность в работе СМО, служит причиной ее перегрузок или недогрузок.

Системы массового обслуживания обладают различной структурой, но обычно в них можно выделить четыре основных элемента: входящий поток требований, накопитель, каналы обслуживания, выходящий поток.

В зависимости от правил образования очереди различают следующие СМО:

1) системы с отказами, в которых при занятости всех каналов обслуживания заявка покидает систему необслуженной;

2) системы с неограниченной очередью, в которой заявка встает в очередь, если в момент ее поступления все каналы обслуживания были заняты;

3) системы с ожиданием и ограниченной очередью, в которой время ожидания ограничено какими-либо условиями или существуют ограничения на число заявок, стоящих в очереди.

Рассмотрим характеристики входящего потока требований.

Определение 1. Поток требований называется стационарным, если вероятность попадания того или иного числа событий на участок времени определенной длины зависит только от длины этого участка.

Определение 2. Поток событий называется потоком без последствий, если число событий, попадающих на некоторый участок времени, не зависит от числа событий, попадающих на другие.

Определение 3. Поток событий называется ординарным, если невозможно одновременное наступление двух или более событий.

Определение 4. Поток требований называется пуассоновским (или простейшим), если он обладает тремя свойствами: стационарен, ординарен и не имеет последствий.

Название связано с тем, что при выполнении указанных условий число событий, попадающих на любой фиксированный интервал времени, будет распределено по закону Пуассона.

Определение 5. Интенсивностью потока заявок λ называется среднее число заявок, поступающих из потока за единицу времени.

Для стационарного потока интенсивность постоянна. Если t - среднее значение интервала времени между двумя соседними заявками, то λ =1/ t. В случае пуассоновского потока вероятность поступления на обслуживание m заявок за промежуток времени t определяется по закону Пуассона:

P_m(t) =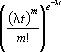

Время между соседними заявками распределено по экспоненциальному закону с плотностью вероятности f(t)= λe^-λt. Время обслуживания t_обсл. является случайной величиной и подчиняется показательному закону распределения с плотностью вероятности f(t)=μ e^-μt, где μ - интенсивность потока обслуживания, т.е. среднее число заявок, обслуживаемых в единицу времени, t_обсл. =1/μ.

Дата добавления: 2014-12-27