Определение задачи линейного программирования (ЗЛП), общая, симметричная и каноническая формы записи задачи линейного программирования

По городской телефонной сети было произведено 100 наблюдений и установлено, что средняя продолжительность телефонного разговора составляет 4 минут при среднеквадратичном отклонении 2 мин. Предельная ошибка выборки с вероятностью 0,954 составляет

Определение искомой характеристики генеральной совокупности внутри какого-то интервала с заданной вероятностью, называется

Вариант дискретного вариационного ряда, имеющий наибольшую частоту, называется

Средним квадратичным отклонением называется

Если количественный признак изменяется непрерывно или принимает много значений, то соответствующий вариационный ряд называется

£ дискретным;

R интервальным;

£ атрибутивным.

R среднее отклонение вариантов от среднего значения.

£ максимальное отклонение вариантов от среднего значения.

£ размах значений признака.

R модой;

£ медианой;

£ средней арифметической величиной.

30. Выборочное наблюдение – это

£ сплошное наблюдение;

R несплошное наблюдение;

£ наблюдение всей генеральной совокупности.

R интервальной оценкой;

£ точечной оценкой;

£ выборочной оценкой;

£ качественной оценкой.

£ 0,2;

£ 0,3;

R0,4;

£ 0,5.

Тема №7.Экономико-математические методы

Исследование операций – научная дисциплина, занимающаяся разработкой и практическим применением методов наиболее эффективного управления различными организационными системами.

Операцией называется совокупность взаимосогласованных действий, направленных на достижение вполне определенной цели.

Оперирующей стороной называются определенные лица и коллективы, объединенные организационным руководством и активно стремящиеся к достижению поставленной цели.

Стратегиями оперирующей стороны в данной операции называются допустимые способы расходования ею имеющихся активных средств. Здесь слово ”допустимые” следует понимать как «не выходящие за пределы технических, организационных, физических возможностей». Среди допустимых обычно находятся и оптимальные стратегии, превосходящие остальные по каким-либо признакам.

Оптимальные (от латинского optimus – наилучший) стратегии должны представлять первоочередной интерес для оперирующей стороны.

Критерием эффективности операции называется показатель требуемого, ожидаемого, достигнутого соответствия между результатом предпринимаемых действий и целью операции. Важнейшей функцией критерия является сравнительная оценка различных стратегий до начала их реализации. Его используют также на завершающем этапе операции для характеристики полученных результатов. Как правило, интерес представляют стратегии, позволяющие достичь максимальных значений критерия.

Состоянием операции в некоторый момент времени t называется совокупность ее характеристик, проявляющихся в этот момент и отражающих объективно сложившееся положение дел. Всякая операция представляет собой процесс, существующий во времени, проходящий различные этапы развития и завершающийся получением конечного результата, сопоставимого с исходной целью.

Математической моделью операции называется формальные соотношения, устанавливающие связь принятого критерия эффективности с действующими факторами операции.

Чтобы построить математическую модель, необходимо оценить количественно проявления рассматриваемых факторов и указать группы рассматриваемых параметров, формально представляющие эти факторы.

Математические модели могут иметь вид формул, систем уравнений или неравенств, а также таблиц, числовых последовательностей, геометрических образов, отражающих зависимость между критерием эффективности операции и теми параметрами, которые представляют учтенные действующие факторы.

Решением, связанным с выбранной математической моделью, называется конкретный набор значений управляемых параметров. Решение можно получить различным путем, с различной степенью точности, в различных предположениях свойств неуправляемых параметров, но независимо от этого оно должно рассматриваться лишь как вспомогательный материал, нуждающийся в осмыслении и сопоставлениях.

Определение 1. Задача, в которой требуется найти экстремум функции

при ограничениях:

,

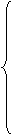
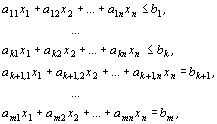
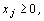
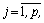
называется общей задачей линейного программирования (ЗЛП).

Задача в краткой записи имеет вид

,

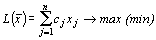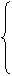
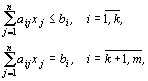
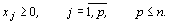
Определение 2. Задача, в которой требуется найти экстремум функции

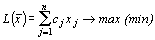
при ограничениях:

,

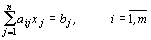называется задачей линейного программирования, заданной в канонической форме.

Определение 3. Задача, в которой требуется найти экстремум функции

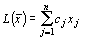
при ограничениях:

,

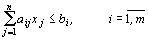называется задачей линейного программирования заданной в симметричной форме записи.

Определение 4. Функция

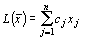
называется целевой функцией ЗЛП.

Определение 5. Совокупность чисел 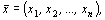удовлетворяющая ограничениям ЗЛП, называется допустимым решением ЗЛП.

Определение 6. Допустимое решение, при котором целевая функция принимает максимальное (минимальное) значение, называется оптимальным решением ЗЛП.

Переход от одной формы ЗЛП к другой

Переход от неканонической формы ЗЛП к канонической.

Теорема 1. Каждому решению 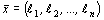неравенства 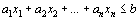соответствует единственное решение 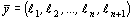уравнения 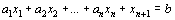и неравенства 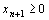, и наоборот.

Из теоремы следует, что неравенство 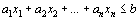можно заменить уравнением 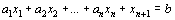и неравенством .

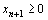Переменную 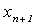называют балансовой переменной.

Следовательно, чтобы привести задачу к каноническому виду, нужно заменить каждое неравенство системы ограничений соответствующим уравнением и неравенством 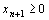, введя в каждое неравенство балансовую переменную с коэффициентом +1, если знак неравенства £, и с коэффициентом -1, если знак неравенства ³. В целевую функцию балансовые переменные вводятся с нулевыми коэффициентами.

Если на переменную 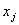не наложено условие на неотрицательность, то эту переменную надо представить в виде разности двух неотрицательных переменных: 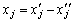, где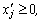

Переход от канонической формы ЗЛП к симметричной форме.

Чтобы перейти от канонической формы ЗЛП к симметричной, нужно найти общее решение системы уравнений:

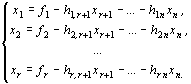
Так как все переменные должны быть неотрицательными, в том числе и базисные, получим систему неравенств:

Чтобы исключить базисные переменные из целевой функции, необходимо в целевую функцию вместо базисных переменных подставить их выражения через свободные переменные.

Пример 1. Дана ЗЛП: найти наибольшее значение функции 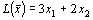при ограничениях:

.

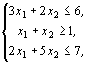
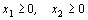Приведем ее к каноническому виду.

Канонический вид задачи: найти наибольшее значение функции 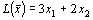при ограничениях:

.

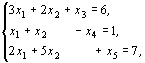
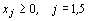Пример 2. Перейти от канонического вида задачи к симметричному. Найти наибольшее значение функции 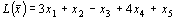при ограничениях:

.

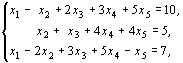
Разрешим систему относительно произвольного базиса, система примет вид

И так как 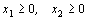, 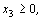отбросив базисные переменные, получим систему неравенств

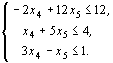
Выразим целевую функцию через свободные переменные:

Симметричный вид задачи: найти наибольшее значение функции 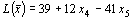при ограничениях:

.

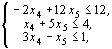
Математические модели экономических задач

Задача об оптимальном использовании ресурсов

Предприятие может выпускать определенные виды продукции, используя для этого различные виды ресурсов. Известны затраты каждого вида ресурса на производство единицы каждого вида продукции и прибыль от реализации единицы каждого вида продукции. Требуется составить план выпуска продукции, чтобы при данных запасах ресурсов получить максимальную прибыль.

Составим математическую модель данной задачи.

Введем обозначения:

i - номер i -го вида ресурса, ;

b_i - запасы i -го вида ресурса, ;

j - номер j -го вида продукции, ;

a_ij - затраты i -го вида ресурса на производство единицы j -го вида продукции;

c_j - прибыль от реализации единицы j -го вида продукции.

Все данные занесем в таблицу:

Виды продукции Виды ресурсов	1 2 … j … n	Запасы ресурсов
… i … m	a 11 a 12 … a 1 j … a 1 n a 21 a 22 … a 2 j … a 2 n … a i1 a i2 … aij … ain … am 1 am 2 … amj … amn	b 1 b 2 … bi … bm
Прибыль от реализации единицы продукции	c 1 c 2 … cj … cn

Обозначим через x_j - планируемый выпуск j -го вида продукции; 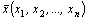- план выпуска продукции. Тогда прибыль от реализации всей выпускаемой продукции составит

c ₁ x ₁ + c ₂ x ₂ +…+ c_jx_j +…+ c_nx_n.

Составим ограничения по ресурсам. Найдем расход первого вида ресурса:

a ₁₁ x ₁+ a ₁₂ x ₂+…+ a _{1 j}х_j +…+ a _{1 n}x_n.

Первый вид ресурса имеется в наличии b ₁ условных единиц, т.е. получаем ограничение a ₁₁ x ₁+ a ₁₂ x ₂+…+ a _{1 j}x_j +…+ a _{1 n}x_n £ b ₁.

Аналогично составляем ограничения по всем остальным видам ресурсов.

Кроме того, x_j ³ 0, , так как количество продукции не может быть отрицательным числом.

Получим ЗЛП: найти наибольшее значение функции 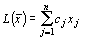при ограничениях:

,

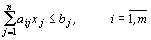Таким образом, математической моделью данной задачи является ЗЛП.

Задача о диете

В продаже имеются различные виды продуктов. Известны содержания питательных веществ в единице каждого вида продукта, цена продуктов, медицинские требования на содержание питательных веществ в суточной диете. Требуется определить, какие продукты и в каком количестве нужно включить в диету, чтобы она соответствовала всем медицинским требованиям и чтобы стоимость диеты была минимальной.

Составим математическую модель данной задачи.

Введем обозначения:

j - номер j -го продукта, ;

i - номер i -го питательного вещества, ;

a_ij -содержание i -го питательного вещества в единице j -го продукта;

b_i - минимальное содержание i -го питательного вещества в суточной диете;

c_j - цена единицы j -го продукта.

Все данные занесем в таблицу:

Виды продуктов   Виды питательных веществ	1 2 … j … n	Медицинские требования к диете
… i … m	a 11 a 12 … a 1 j … a 1 n a 21 a 22 … a 2 j … a 2 n … ai 1 ai 2 … aij … ain … am 1 am 2 … amj … amn	b 1 b 2 … bi … bm
Цена единицы продукта	c 1 c 2 … cj … cn

Пусть x_j единиц j -го продукта включается в суточную диету, тогда 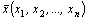- суточная диета.

Цена диеты:

c ₁ x ₁ + c ₂ x ₂ +…+ c_nx_{n .}

Если в диету включаем x ₁, x ₂, …, x_n единиц каждого продукта, то содержание первого питательного вещества в диете составит

a ₁₁ x ₁+ a ₁₂ x ₂+…+ a _{1 j}x_j +…+ a _{1 n}x_n,

и это должно быть не менее чем b ₁ единиц, т.е. получаем неравенство

a ₁₁ x ₁+ a ₁₂ x ₂+…+ a _{1 j} x_j +…+ a _{1 n} x_n ³ b ₁.

Аналогично составляем ограничения по всем видам питательных веществ.

Кроме того, x_j ³ 0, так как количество продуктов не может быть отрицательным числом.

Математическая модель задачи: найти минимум функции

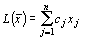
при ограничениях:

,

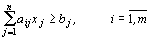Таким образом, математической моделью данной задачи является ЗЛП.

Задача на оптимальный раскрой материала (по длине)

Имеются прутки одинаковой длины, из которых нужно нарезать определенное количество заготовок заданной длины. Прутки можно нарезать на заготовки по различным вариантам. При каждом варианте нарезания прутков остаются концевые отрезки.

Требуется определить, какое количество прутков следует разрезать по каждому варианту, чтобы получить заданное количество заготовок различной длины и чтобы общая длина концевых отрезков была минимальной.

Составим математическую модель данной задачи.

Введем обозначения:

i - номер i -го вида заготовки, ;

j - номер j -го варианта раскроя прутка, ;

a_ij - количество заготовок i -го вида, получаемых из одного прутка, разрезаемого по j -му варианту;

b_i - требуемое число заготовок i -го вида;

c_j - длина концевого отрезка, оставшегося от одного прутка при разрезании прутка по j -му варианту.

Все данные занесем в таблицу:

Варианты Раскроя Виды заготовок	1 2 … j … n	План по заготовкам
… i … m	a 11 a 12 … a 1 j … a 1 n a 21 a 22 … a 2 j … a 2 n … ai 1 ai 2 … aij … ain … am 1 am 2 … amj … amn	b 1 b 2 … bi … bm
Длина концевого отрезка	c 1 c 2 … cj … cn

Обозначим через х_j - число прутков, разрезаемых по j- муварианту, тогда 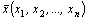- план раскроя прутков. Найдем общую длину концевых отрезков.

По первому варианту планируем разрезать x ₁ прутков, концевой отрезок от одного прутка будет иметь длину с ₁, тогда общая длина концевых отрезков от х ₁ прутков составит c ₁ x ₁. Аналогично, общая длина концевых отрезков от х ₂ прутков, разрезанных по второму варианту, будет равна c ₂ x ₂ и т.д.

Следовательно, общая длина концевых отрезков при разрезании прутков по всем вариантам

.

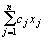Составим ограничения по заготовкам.

Заготовок первого вида получают из одного прутка, разрезаемого по первому варианту, a ₁₁ штук, а из x ₁ прутков - a ₁₁ x ₁; по второму варианту из одного прутка получают a ₁₂ штук, а из x ₂ прутков - a ₁₂ x ₂ и т.д., по n -му варианту - a _{1 n}x_n штук. Отсюда получаем первое ограничение

a ₁₁ x ₁+ a ₁₂ x ₂+…+ a _{1 n}x_n = b _1.

Аналогично получаем ограничения по всем заготовкам.

Кроме того, 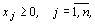так как число прутков не может быть отрицательным.

Математическая модель задачи: найти наименьшее значение функции

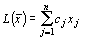
при ограничениях:

,

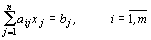Таким образом, математической моделью данной задачи является ЗЛП.

Пример 1. Имеются прутки длиной 1 м. Требуется нарезать 200 заготовок длиной 25 см, 250 заготовок длиной 30 см и 150 заготовок длиной 35 см. Количество заготовок, которые можно нарезать из одного прутка по различным вариантам, а также длина концевых отрезков даны в таблице:

Варианты раскроя Виды заготовок										План на заготовки
1 (25 см)
2 (30 см)
3 (35 см)
Длина концевого отрезка, см

Требуется определить, сколько прутков необходимо разрезать по каждому варианту, чтобы выполнить план по заготовкам и чтобы общая длина концевых отрезков была минимальной.

Составим математическую модель задачи.

Пусть x_j - количество прутков, разрезанных по j -му варианту, 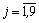, тогда 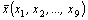- план раскроя.

Найдем общую длину концевых отрезков, для этого длину концевого отрезка, оставшегося от одного прутка, умножим на количество прутков, разрезаемых по данному варианту. Получим

0 х ₁+10 х ₂+0 х ₃+5 х ₄+10 х ₅+20 х ₆+15 х ₇+5 х ₈+15 х ₉.

Тогда целевая функция запишется так:

.

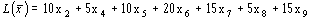Составим ограничения по заготовкам, для этого количество заготовок, полученных из одного прутка, умножим на число прутков, разрезаемых по данному варианту, т.е.

4 х ₁ + х ₄+ х ₅+2 х ₆+2 х ₇+ х ₉,

а всего заготовок первого вида требуется 200 штук. Получим уравнение

4 х ₁ + х ₄+ х ₅+2 х ₆+2 х ₇+ х ₉ = 200.

Аналогично получим ограничения по второму и третьему виду заготовок:

3 х ₂+ х ₃ + х ₅+ х ₆ +2 х ₈+2 х ₉ =250,

2 х ₃+2 х ₄ + х ₅ + х ₇ + х ₈ = 150.

Кроме того, 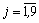, так как число прутков не может быть отрицательным. Математическая модель задачи: найти наименьшее значение функции

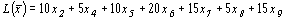
при ограничениях:

.

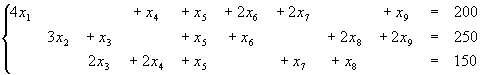
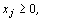
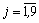Пример 2. Для производства двух видов продукции используется три вида сырья. Расход сырья на производство единицы каждого вида продукции, запасы, а также прибыль от реализации единиц каждого вида сырья заданы в таблице:

Виды Виды продукции сырья	1 2	Запасы сырья, кг
	3 8 4 5 9 4
Прибыль от реализации единицы продукции, у.е.	2 3

Составить план выпуска продукции, дающий максимальную прибыль.

Для этого составим математическую модель задачи: обозначим через х ₁, х ₂ - планируемый выпуск продукции.

Найдем прибыль: 2 х ₁ (у.е.) - это прибыль от х ₁ единиц первого вида продукции и 3 х ₂ (у.е.) - прибыль от х ₂ единиц второго вида продукции, а всего 2 х ₁+3 х ₂ - прибыль от реализации х ₁ единиц первого вида продукции и х ₂ единиц второго вида продукции.

Составим ограничение по первому виду сырья:

3 х ₁+8 х ₂ - расход первого вида сырья на выпуск х ₁ единиц первого вида продукции и х ₂ единиц второго вида продукции, а всего первого вида сырья имеется 240, следовательно, получим неравенство 3 х ₁+8 х ₂ £ 240.

Аналогично, по второму и третьему видам сырья:

4 х ₁+5 х ₂ £ 200,

9 х ₁+4 х ₂ £ 360.

Кроме того, х ₁ ³0, х ₂ ³0, так как количество выпускаемой продукции не может быть отрицательным числом.

Математическая модель задачи: найти наибольшее значение функции

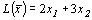
при ограничениях:

х ₁ ³0, х ₂ ³0.

Дата добавления: 2014-12-27