
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Графический метод и симплекс-метод решения задач линейного программирования
|
|
|
|
Графический метод решения ЗЛП
Графическим методом можно решать задачи, заданные в неканоническом виде с двумя переменными или сводящиеся к ним. Рассмотрим задачу следующего вида: найти экстремум функции

при ограничениях:
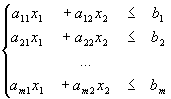
х 1>0, х 2>0.
Надо построить область допустимых решений системы ограничений. При этом возможны случаи:
1) область допустимых решений - пустое множество;
2) область допустимых решений - единственная точка;
3) область допустимых решений - выпуклый многоугольник;
4) область допустимых решений - выпуклая неограниченная область.
В первом случае ЗЛП не имеет оптимального решения из-за несовместности системы ограничений.
Во втором случае - это единственное решение и будет оптимальным решением.
В третьем случае, чтобы найти оптимальное решение задачи, можно найти координаты всех угловых точек многоугольника, вычислить значения целевой функции во всех угловых точках. Наибольшее из этих значений и будет максимальным значением целевой функции, а наименьшее - минимальным, а координаты соответствующей угловой точки - оптимальным решением.
Существует другой способ, который позволяет графически сразу найти угловую точку, соответствующую оптимальному решению.
Пусть с 0 - некоторое число. Прямая 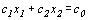 является линией уровня целевой функции. В каждой точке этой прямой целевая функция принимает одно и то же значение, равное с 0. Вектор - градиент целевой функции
является линией уровня целевой функции. В каждой точке этой прямой целевая функция принимает одно и то же значение, равное с 0. Вектор - градиент целевой функции
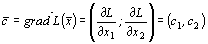
перпендикулярен к линиям уровня и показывает направление, в котором эта функция возрастает с наибольшей скоростью. Выбирая из линий уровня, проходящих через область допустимых решений, наиболее удаленную в направлениях вектора  (в случае минимизации - в противоположном направлении), определим угловую точку, в которой целевая функция принимает максимальное (минимальное) значение.
(в случае минимизации - в противоположном направлении), определим угловую точку, в которой целевая функция принимает максимальное (минимальное) значение.
Если экстремум достигается в двух угловых точках, то, по теореме об альтернативном оптимуме, оптимальным решением будет любая точка отрезка, соединяющего эти точки:
 ,
,  .
.
В четвертом случае, когда область допустимых решений системы ограничений задачи неограниченная выпуклая область, оптимальное решение находится аналогично описанному выше. В данном случае оптимальное решение может совпадать с одной угловой точкой, с двумя угловыми точками и оптимальное решение может и не существовать из-за неограниченности целевой функции сверху в задаче на максимум или снизу в задаче на минимум.
Пример 1. Решить графически следующую задачу:
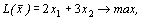 ,
,

х 1 >0, х 2 >0.
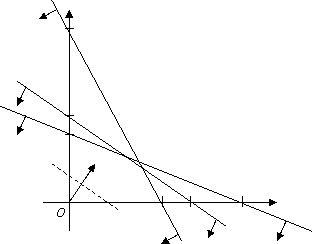
Построим область допустимых решений системы ограничений:
Х 2
30 А
В
С
D Х 1
40 50 80
l 2 l 1
l 3
Областью допустимых решений системы ограничений является выпуклый пятиугольник ОАВCD.
Построим вектор 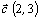 и линию уровня, перпендикулярную вектору
и линию уровня, перпендикулярную вектору 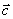 . Наибольшее значение целевая функция достигает в угловой точке В. Найдем координаты точки В, для этого решим систему из уравнений первой и второй прямой.
. Наибольшее значение целевая функция достигает в угловой точке В. Найдем координаты точки В, для этого решим систему из уравнений первой и второй прямой.
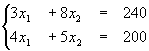
Решая систему, получим: 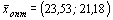 ,
, 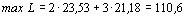 .
.
Пример 2. Найти наибольшее и наименьшее значения функции
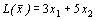
при ограничениях:
 х 1+ х 2 > 8,
х 1+ х 2 > 8,
-5 х 1+2 х 2 < 10,
х 1-3 х 2 < 0,
х 1 >0, х 2 >0
Построим ОДР.

Областью допустимых решений системы ограничений является выпуклая многоугольная неограниченная область. Наименьшее значение целевой функции достигается в угловой точке А, а наибольшее значение функции найти нельзя, так как функция не ограничена сверху, т.е. max L = ∞.
 Найдем координаты точки А, для этого решим систему из уравнений первой и третьей прямой:
Найдем координаты точки А, для этого решим систему из уравнений первой и третьей прямой:
х 1+ х 2 = 8,
х 1-3 х 2 =0
х 1 = 6, 
х 2 = 2.
т.е.  .
.
Симплексный метод
Симплексный метод, или метод последовательного улучшения решения, универсален, им можно решить любую ЗЛП.
Пусть ЗЛП задана в канонической форме:
 (1)
(1)
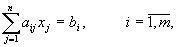 (2)
(2)
 (3)
(3)
Разрешим систему уравнений (2) относительно неотрицательного базиса. Пусть система (2) при этом примет вид

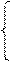
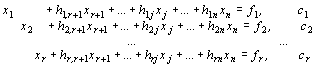 (4)
(4)
Получено опорное решение  .
.
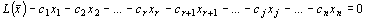 . (5)
. (5)
Исключим базисные переменные х 1, х 2, …, хr из целевой функции, для этого умножим первое уравнение системы (4) на с 1, второе на с 2 и т.д., r -е уравнение умножим на сr и все это прибавим к целевой функции. Получим:
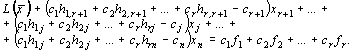 (6)
(6)
Определение 1. Выражение (6) называется приведенным выражением для целевой функции, коэффициенты при свободных переменных хr+ 1, …, хj, …, хn называются оценками и обозначаются D.
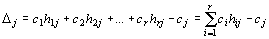 . (7)
. (7)
Правая часть уравнения (6)
 ,
,
так как 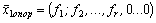 .
.
Тогда уравнение (6) примет вид
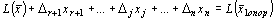 . (8)
. (8)
Запишем систему (5) и выражение (8) в виде одной системы и перейдем ко второму опорному решению:

 (9)
(9)
 .
.
Допустим, что вместо xi в базис вводится свободная переменная xj. По правилу прямоугольника найдем значение целевой функции от второго опорного решения.
 (10)
(10)
Сравним 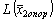 и
и  , так как fi ³0, hij > 0, то знак дроби
, так как fi ³0, hij > 0, то знак дроби 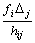 зависит от знака оценки Dj.
зависит от знака оценки Dj.
1) Если D j > 0, то  .
.
2) Если D j < 0, то 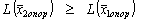 .
.
3) Если D j = 0, то 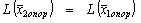 .
.
Отсюда получаем критерий оптимальности для ЗЛП на максимум:
1) если все оценки D j > 0, то найденное решение оптимальное;
2) если среди оценок имеется хотя бы одно отрицательное число, то найденное решение не оптимально.
Пусть Dj < 0, тогда если среди коэффициентов при хj есть хотя бы одно положительное число, хj можно ввести в базис и 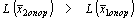 .
.
Если D j < 0 и все коэффициенты при хj hij < 0, то хj в базис ввести нельзя. Покажем, что 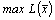 в этом случае равен бесконечности, для этого из системы (9) выпишем общее решение, всем свободным переменным, кроме хj, придадим значение, равное 0, получим
в этом случае равен бесконечности, для этого из системы (9) выпишем общее решение, всем свободным переменным, кроме хj, придадим значение, равное 0, получим
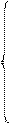
 (11)
(11)
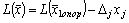 . (12)
. (12)
Отсюда видно, что если хj придавать сколь угодно большие числовые значения, то решение, полученное из системы (11), будет допустимым, а значение целевой функции (12) будет неограниченно расти, т.е. при х → ∞ 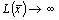 ;
;
3) предположим, что найдено оптимальное решение задачи, т.е. все оценки неотрицательны, и хотя бы одна из оценок свободных переменных равна нулю. Это говорит о наличии в задаче альтернативного оптимума. Если ввести в базис свободную переменную с нулевой оценкой, то получим второе опорное оптимальное решение, а значение целевой функции при этом не изменится.
Если нулевых оценок свободных переменных окажется несколько, то введение в базис каждой из этих переменных приводит к получению различных опорных оптимальных решений. Тогда задача имеет множество оптимальных решений, каждое из которых является выпуклой линейной комбинацией опорных оптимальных решений.
Алгоритм симплексного метода
Решение задач линейного программирования симплексным методом предполагает следующие этапы:
1) привести задачу к каноническому виду;
2) найти неотрицательное базисное решение системы ограничений;
3) найти оценки свободных переменных по формуле

и записать полученные оценки в симплексную таблицу;
проверить найденное опорное решение на оптимальность: если требуется найти максимум целевой функции, то:
а) если все оценки Dj > 0, то найденное решение оптимально и задача решена;
б) если хотя бы одна оценка Dj < 0, а при соответствующей переменной х j нет ни одного положительного коэффициента, то задача не имеет оптимального решения из-за неограниченности целевой функции;
в) если хотя бы одна оценка Dj < 0, а при соответствующей переменной х j есть хотя бы один положительный коэффициент, то найденное решение не оптимально и его можно улучшить. Если отрицательных оценок несколько, то в базис вводят переменную с наибольшей по абсолютной величине отрицательной оценкой;
4) если выполняется случай в), то нужно перейти к следующему опорному решению;
5) перейти к п. 3.
Замечание 1. Критерием оптимальности для ЗЛП на минимум является неположительность оценок, т.е. все D j < 0,  .
.
Замечание 2. В ЗЛП максимум и минимум целевой функции понимаются как глобальные.
Пример 3. Найти наибольшее значение функции
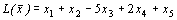
при ограничениях:

х 1-2х2 - 2х3 + х 4 - х 5 = 1,
-2 х 2 - х 3 +3х4 + х 5 = 5,
х2 + 8 х 3+ х 4 +3 х 5 = 20,
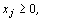
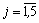 .
.
Задача задана в каноническом виде. Найдем исходное опорное решение.
| № п/п | Б.п. | х 1 | х 2 | х 3 | х 4 | х 5 | b i |
| x 1 | -2 -2 1 | -2 -1 | -1 | ||||
| x 1 x 2 | 8 | ||||||
| x 1 x 5 x 2 | 37/8 15/8 19/8 | -1/8 5/8 -7/8 | 103/8 45/8 25/8 |
 .
.
Проверим это решение на оптимальность.
| № п/п | сj | Б.п. | -5 | bi | ||||
| х 1 | х 2 | х 3 | х 4 | х 5 | ||||
| x 1 x 5 x 2 | 37/8 15/8 19/8 | -1/8 5/8 -7/8 | 103/8 45/8 25/8 | |||||
| D j | 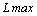
| 111/8 | -19/8 | 173/8 |
Найденное решение не оптимально, так как D4 < 0. Введем в базис свободную переменную с отрицательной оценкой х 4.
| № п/п | сj | Б.п. | -5 | bi | ||||
| х 1 | х 2 | х 3 | х 4 | х 5 | ||||
| x 1 x 4 x 2 | 1/5 8/5 7/5 | |||||||
| D j | 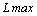
| 19/5 |
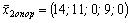 . Так как среди оценок нет отрицательных чисел, то второе опорное решение оптимально.
. Так как среди оценок нет отрицательных чисел, то второе опорное решение оптимально.
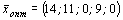 ,
, 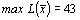 .
.
Метод искусственного базиса
При решении задач линейного программирования симплексным методом необходимо систему ограничений привести к единичному неотрицательному базису. Метод искусственного базиса дает возможность решать задачи без предварительного нахождения опорного решения.
Дана задача: найти наибольшее значение функции

при ограничениях:

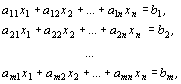
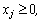
 .
.
Составим расширенную задачу, которую назовем М-задачей.
Найти наибольшее значение функции

при ограничениях:

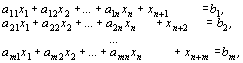
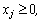
 .
.
В каждое уравнение, в котором нет базисной переменной, вводим переменную 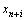 , где
, где  , с коэффициентом 1, эти переменные называются искусственными, и они образуют искусственный базис. Искусственные переменные вводятся в целевую функцию с коэффициентами -М, если задача решается на максимум, и +М, если задача решается на минимум, где М сколь угодно большое положительное число. Система ограничений расширенной задачи совместна.
, с коэффициентом 1, эти переменные называются искусственными, и они образуют искусственный базис. Искусственные переменные вводятся в целевую функцию с коэффициентами -М, если задача решается на максимум, и +М, если задача решается на минимум, где М сколь угодно большое положительное число. Система ограничений расширенной задачи совместна.
Исходное опорное решение 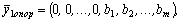 где
где 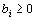 ,
,  .
.
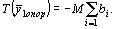
Между допустимыми решениями исходной и М-задачи есть связь. Если 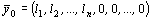 - допустимое решение М-задачи, то
- допустимое решение М-задачи, то 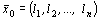 - допустимое решение исходной задачи, причем
- допустимое решение исходной задачи, причем
 .
.
Эти решения называются соответствующими.
Теорема.
1. Если в оптимальном решении М-задачи 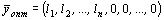 все искусственные переменные равны 0, то соответствующее ему решение
все искусственные переменные равны 0, то соответствующее ему решение  является оптимальным решением исходной задачи.
является оптимальным решением исходной задачи.
2. Если в оптимальном решении М-задачи хотя бы одна из искусственных переменных не равна 0, то система ограничений исходной задачи несовместна.
3. Если М-задача не имеет оптимального решения, то и исходная задача также не имеет оптимального решения.
Алгоритм метода искусственного базиса
1. Задачу линейного программирования привести к каноническому виду.
2. Построить М-задачу.
3. Решить М-задачу симплексным методом, при этом оценки свободных переменных находятся по формуле 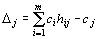 . Они состоят из двух слагаемых, одно из которых содержит М. Поэтому их будем записывать в двух строках
. Они состоят из двух слагаемых, одно из которых содержит М. Поэтому их будем записывать в двух строках  и
и 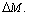

4. Применяя теорему о связи между оптимальными решениями М-задачи и исходной задачи, даем ответ исходной задачи:
а) если в оптимальном решении М-задачи все искусственные переменные равны 0, то соответствующее решение исходной задачи является оптимальным и экстремумы целевых функций равны;
б) если в оптимальном решении М-задачи хотя бы одна из искусственных переменных не равна 0, то исходная задача не имеет оптимального решения из-за несовместности системы ограничений;
в) если М-задача не имеет оптимального решения, то исходная задача также не имеет оптимального решения.
Целочисленное программирование
В некоторых экономических задачах (например, при определении оптимального выпуска машин, агрегатов, размещения оборудования) переменные характеризуют физически неделимые единицы и поэтому должны принимать только целые значения.
Формулировка задачи целочисленного программирования: найти наибольшее значение функции
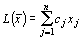
при ограничениях:
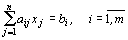 ,
,
 , хj - целые,
, хj - целые, 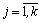 .
.
Если k = n, то задача полностью целочисленная.
Если k не равно n, то задача является частично целочисленной.
Методы решения задач линейного программирования не гарантируют целочисленности решения.
Иногда задачи целочисленного программирования решают приближенно. Отбросив условие целочисленности, решают задачу методом линейного программирования, затем в полученном оптимальном решении округляют переменные до целых чисел. Такой прием можно использовать, если значения переменных достаточно велики и погрешностью округления можно пренебречь. Если значения переменных невелики, то округление может привести к значительному расхождению с оптимальным решением. Существует аналитический метод решения полностью целочисленных задач - метод Гомори.
Метод Гомори
Основная идея решения целочисленных задач, первоначально предложенная Данцигом, Фулкерсоном и Джонсоном, заключается в том, что задача сначала решается без ограничения целочисленности. Если решение получается целочисленным, то задача решена, если нет, то к задаче присоединяют новое дополнительное ограничение, которое называют сечением. Получают новую задачу, для которой множество допустимых решений будет меньше, чем для исходной задачи, но будет содержать все допустимые целочисленные решения.
Дополнительное ограничение отсекает часть области, содержащую нецелочисленное оптимальное решение.
Вновь полученную задачу решают методом линейного программирования. Процесс построения сечений и решения задачи повторяется до получения целочисленного оптимального решения. Общий систематический способ построения сечений разработал Гомори в 1958 г.
Алгоритм метода Гомори
Пусть дана полностью целочисленная задача линейного программирования: найти максимальное значение функции
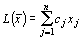
при ограничениях:
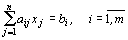 ,
,
 , хj - целые,
, хj - целые,  .
.
1) Отбросив условие целочисленности, решаем исходную задачу симплексным методом. Если получится целочисленное оптимальное решение, то задача решена. Если в оптимальном решении не все переменные целочисленны, то строим сечения.
2) Пусть в оптимальном решении переменная x t - дробное число, т.е. x t= f t. Рассмотрим уравнение, в котором x t - базисная переменная.
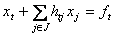 , (1)
, (1)
где J - множество индексов свободных переменных.
Разобьем все коэффициенты и свободный член (1) на два слагаемых: целую и дробную часть. Целой частью числа а называется наибольшее целое число, не превышающее а. Дробной частью числа а называется разность между числом а и его целой частью. Целую часть числа обозначим [а], а дробную часть – {а}, т.е. а = [а]+{а}. Тогда уравнение (1) примет вид
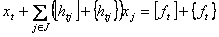 , (2)
, (2)
или
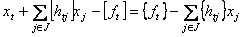 .
.
Для любого целочисленного решения задачи левая часть уравнения (2) есть целое число, следовательно, и правая часть также будет целым числом.
Неравенство
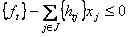 (3)
(3)
является сечением Гомори.
Покажем, что любое целочисленное решение задачи удовлетворяет этому неравенству, а нецелочисленное решение ему не удовлетворяет. Пусть 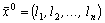 - целочисленное решение, и предположим, что оно не удовлетворяет неравенству (3), т.е.
- целочисленное решение, и предположим, что оно не удовлетворяет неравенству (3), т.е.
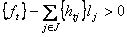 , или
, или 
по условию lj > 0, 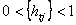 , отсюда
, отсюда 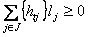 , кроме того,
, кроме того,  . Получим
. Получим
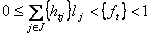 , или
, или  , т.е. является дробным числом.
, т.е. является дробным числом.
Подставив 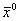 в уравнение (2), получим
в уравнение (2), получим
 .
.
Правая часть уравнения - дробное число, а левая часть - целое число. Получили противоречие. Следовательно, любое целочисленное решение задачи удовлетворяет неравенству (3).
Покажем, что нецелочисленное оптимальное решение не удовлетворяет неравенству (3).
Пусть 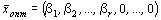 - нецелочисленное оптимальное решение задачи. Подставим его в неравенство (3):
- нецелочисленное оптимальное решение задачи. Подставим его в неравенство (3):
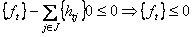 , но
, но 
Следовательно, 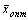 не удовлетворяет неравенству (3).
не удовлетворяет неравенству (3).
3) Присоединяя неравенство (3) к ранее решенной задаче, получим новую задачу линейного программирования, которую вновь решаем симплексным методом; если ее оптимальное решение окажется целочисленным, то оно и будет оптимальным решением исходной задачи. Если снова получится нецелочисленное решение, то строим новое сечение, и т.д.
Замечание. Если в оптимальном решении несколько переменных нецелочисленные, то сечение строят по базисной переменной, имеющей наибольшую дробную часть.
Пример. Найти наибольшее значение функции

при ограничениях:
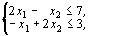
х 1 > 0, х 2 > 0, х 1, х 2 - целые.
Решим задачу симплексным методом без учета целочисленности, для этого приведем ее к каноническому виду
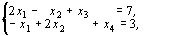
х j > 0, 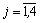 .
.
| № п/п | сj | Б.п. | |||||
| x 1 | x 2 | x 3 | x 4 | bi | |||
| x 4 x 5 | 2 -1 | -1 | |||||
| D j | 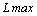
| -2 | -2 | ||||
| x 1 x 4 | -1/2 3/2 | 1/2 1/2 | 7/2 13/2 | ||||
| D j | 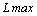
| -3 | |||||
| x 1 x 2 | 2/3 1/3 | 1/3 2/3 | 17/3 13/3 | ||||
| D j | 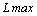
|
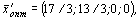 max L = 20.
max L = 20.
Решение нецелочисленное, поэтому строим сечение Гомори. Возьмем первое уравнение из последней симплексной таблицы, так как у х 1 наибольшая дробная часть  .
.
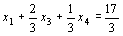 .
.
Сечение примет вид 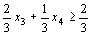 или
или
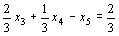 , где х 5>0.
, где х 5>0.
Присоединив это дополнительное ограничение к ограничениям последней симплексной таблицы, получим новую задачу:
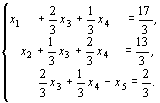

Решим эту задачу симплексным методом.
| № п/п | сj | Б.п. | ||||||
| x 1 | x 2 | x 3 | x 4 | х5 | bi | |||
| х 1 x 2 | 2/3 1/3 2/3 | 1/3 2/3 1/3 | -1 | 17/3 13/3 2/3 | ||||
| x 1 x 2 х 3 | 1/2 1/2 | 1/2 -3/2 | ||||||
| D j | 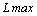
|
 max L = 18.
max L = 18.
Это решение целочисленное, значит исходная задача решена.
max L = 18, 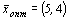 .
.
Дадим геометрическую иллюстрацию метода Гомори. Областью допустимых решений является четырехугольник ОАВС. Оптимальное решение задачи совпадает с точкой 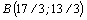 .
.
Построили сечение х 1 < 5, оно отсекает нецелочисленное оптимальное решение. Получили область допустимых решений ОАDЕС. Оптимально решение второй задачи будет в точке D (5, 4). Решение получилось целочисленным, следовательно, исходная задача решена.

|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 3956; Нарушение авторских прав?; Мы поможем в написании вашей работы!