Частные случаи перспективных построений

Деление отрезков на равные и неравные части в перспективе. Геометрические построения при делении отрезков на неравные части основаны на том, что параллельные прямые делят стороны угла в пропорциональном соотношении. Так если требуется разделить на произвольное количество неравных частей горизонтально расположенный отрезок (в качестве примера взят отрезок АВ на рисунке 37), то процесс построений ведется следующим образом. От ближайшей к зрителю точки А данного отрезка откладывается его натуральная величина Аb, разделенная точками 1, 2 и 3 в нужной пропорции[2]. Затем из точки b через точку В проводится прямая до пересечения с линией горизонта в точке V. Далее точки 1, 2 и 3 соединяются прямыми с точкой V, которая соответственно, является их точкой схода. Эти прямые пересекают отрезок АВ в точках 1', 2' и 3', которые делят его в искомой пропорции.

Деление на неравные части отрезка расположенного под произвольным углом к предметной плоскости показано на рисунке 38. Допустим, дан отрезок АВ и его горизонтальная проекция Аb' и требуется разделить этот отрезок на произвольное количество частей в перспективе.

Деление можно осуществить двумя способами. Первый состоит в том, что сначала делится на нужное количество отрезков горизонтальная проекция Аb' аналогично тому, как это сделано на предыдущем рисунке. От построенных таким образом точек 1' и 2' проводятся вертикальные прямые, пересекающие отрезок АВ в точках 1'' и 2'', которые разделяют его в требуемом соотношении.

Второй способ предполагает, что сначала строится точка схода прямой, заключающей в себе отрезок АВ. Для этого от точки схода F прямой Ab' проводится вверх вертикальный луч до пересечения с прямой АВ. Точка пересечения является точкой схода F1 прямой АВ. Далее от точки V (она строится так же, как и в предыдущем случае) проводится вверх вертикальный луч до пересечения с

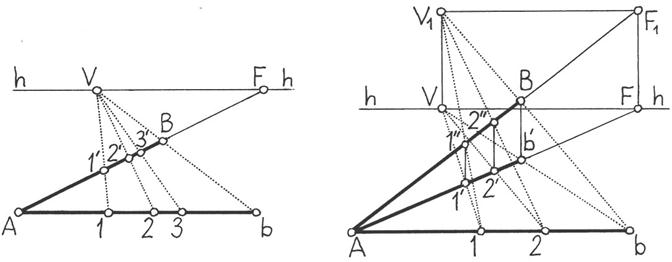
Рисунок 37 - Деление на неравные Рисунок 38 - Деление на неравные

части горизонтального отрезка части отрезка, расположенного

под произвольным углом к

предметной плоскости

горизонтальной прямой, проведенной из точки F1. К полученной таким образом точке V1 проводятся прямые из точек 1 и 2, которые пересекают прямую АВ в искомых точках 1'' и 2''. К сказанному можно добавить, что точка V1 может быть найдена другим способом – она располагается на пересечении прямой Bb и вертикального отрезка, проведенного из точки V.

Построение кривых линий в перспективе. Допустим, требуется построить перспективу показанной на рисунке 39 кривой линии, которую при этом следует изобразить так, чтобы она была расположена в вертикальной плоскости под некоторым углом к картинной плоскости.

Общий смысл построения состоит в том, что на заданной кривой отмечается произвольное количество точек, после чего находится их положение в перспективе и по найденным точкам вычерчивается кривая в пространстве. На рисунке 39 обозначено одиннадцать точек кривой, среди которых имеется пять пар симметричных точек.

Для выполнения дальнейших построений вокруг кривой строится прямоугольник, вершины которого обозначены точками I, II, III и IV, при этом точки 1, 3, 4, 8, 9 и 11 в данном случае обозначены в местах касания кривой к сторонам прямоугольника. На стороне I-IV прямоугольника откладываются точки 2', 4', 5', 6', 7', 8' и 10', полученные путем вертикального параллельного переноса точек 2, 4, 5, 6, 7, 8 и 10. Кроме того, на стороне I-II прямоугольника откладываются точки 2'', 5'' и 6'', полученные путем горизонтального параллельного переноса точек 2, 5 и 6.

Далее начинается построение прямоугольника и вписанной в него кривой в перспективе (рисунок 40). Для того чтобы не усложнять построение, можно считать, что прямоугольник своей ближайшей к зрителю вертикальной стороной касается картинной плоскости, и эта сторона вычерчивается без сокращения в перспективе.

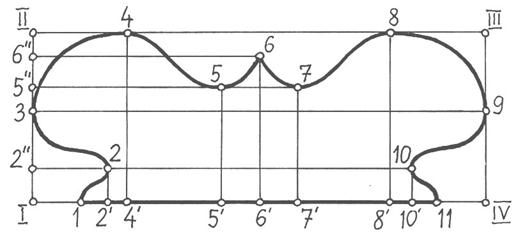
Рисунок 39 – Предварительный этап построения кривой линии в перспективе

Вначале по описанному выше принципу деления отрезков на неравные части строится уходящая в глубину сторона I-IV и на ней отмечаются точки 1, 2', 4', 5', 6', 7', 8', 10' и 11. Затем проводится вертикальный отрезок I-II и на нем отмечается положение точек 2'', 3, 5'' и 6''. Из точек II, 2'', 3, 5'' и 6'' проводятся прямые в расположенную на линии горизонта точку схода F (для экономии места точка F расположена за пределами рисунка), а из точек 2', 4', 5', 6', 7', 8', 10' и IV проводятся вертикальные лучи, в местах пересечения которых с этими прямыми располагаются искомые точки кривой 2, 4, 5, 6, 7, 8, 9, 10, а также точка III. На завершающем этапе остается плавно соединить полученные точки. При необходимости по аналогичному принципу могут быть дополнительно построены любые другие точки кривой.

Построение параллельных прямых при недоступной точке схода в угловой перспективе. При выполнении графических изображений интерьера или архитектурного пейзажа нередко возникает необходимость построить перспективу параллельных прямых, точка схода которых расположена за пределами чертежа – такая ситуация может, например, возникнуть при построении параллельных рядов окон или карнизов зданий в угловой перспективе. Ниже описаны наиболее простые способы выполнения подобных построений.

Построение параллельных прямых при недоступной точке схода может быть осуществлено при условии, что известно перспективное расположение как минимум двух параллельных прямых, либо одной прямой и линии горизонта.

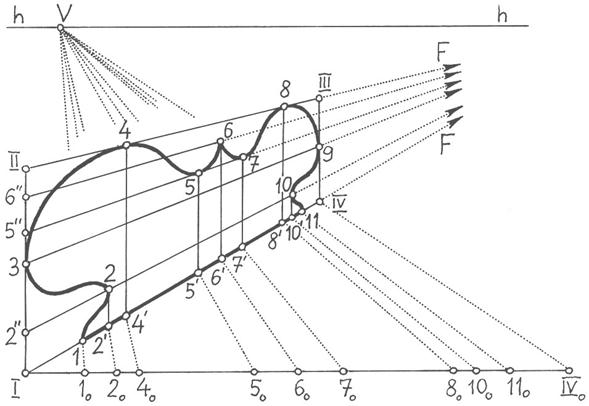
Рисунок 40 – Завершающий этап построения кривой линии в перспективе

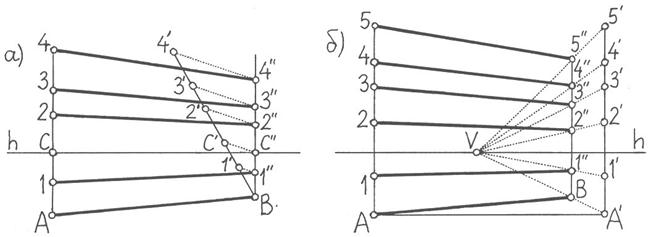
Рисунок 41 – Построение параллельных отрезков при недоступной точке схода в угловой перспективе

Допустим, на изображении задано перспективное расположение горизонтального отрезка АВ и линии горизонта (рисунок 41а). Требуется построить в перспективе прямые параллельные АВ и проходящие через точки 1, 2, 3 и 4 на вертикальном отрезке А-4.

Для выполнения дальнейших построений в месте пересечения отрезка А-4 с линией горизонта отмечается точка С. Далее из точки В проводится вертикальный луч, в месте пересечения которого с линией горизонта отмечается точка С'', после чего под произвольным углом к лучу вычерчивается отрезок В-4', равный А-4. На отрезке В-4' откладываются точки 1', С', 2' и 3', разделяющие его в той же пропорции, в которой разделен точками отрезок А-4.

Далее точка С' соединяется с точкой С'', после чего через точки 1', 2', 3' и 4' проводятся прямые, параллельные С'С''. Эти прямые пересекают вертикальный луч, проведенный из точки В, в точках 1'', 2'', 3'' и 4''. Через эти точки, как показано на рисунке, проходят параллельные прямые 1-1'', 2-2'', 3-3'' и 4-4'', перспективу которых требовалось построить.

На рисунке 41б показан другой способ решения аналогичной задачи. Откладывается горизонтальный отрезок АА' произвольной длины и от точки А' проводится вертикальный отрезок, разделенный точками от 1' до 5' в той же пропорции, что отрезок А-5. Далее проводится прямя А'В до пересечения с линией горизонта в точке V, после чего из точек 1', 2', 3', 4' и 5' проводятся прямые в точку схода V. Эти прямые пересекают вертикальный луч, проведенный из точки В, в искомых точках 1'', 2'', 3'', 4'' и 5'', после чего остается провести прямые через данные точки и точки с соответствующими номерами на отрезке А-5.

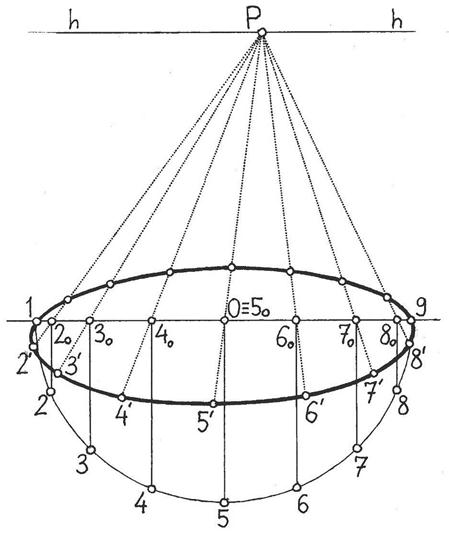
Рисунок 42 – Деление окружности на равные части в угловой перспективе

Деление окружности на равные части в перспективе. Решение этой задачи можно рассмотреть на примере горизонтально расположенной окружности с центром в точке О (рисунок 42). Вначале вычерчивается фронтально расположенная полуокружность такого же диаметра с центром в точке О. Эта полуокружность делится на нужное количество равных частей (в данном случае места делений обозначены цифрами от 1 до 9). Затем из точек 2, 3, 4, 5, 6, 7 и 8 проводятся вверх перпендикуляры к диаметру окружности, пересекающие его в точках 20, 30, 40, 50, 60, 70 и 80. Через эти точки проводятся прямые в точку Р, пересекающие окружность в точках 2', 3', 4', 5', 6', 7' и 8'. Эти точки вместе с симметричными им относительно фронтального диаметра точками, а также точками 1 и 9 обозначают искомые места делений окружности на равные части.

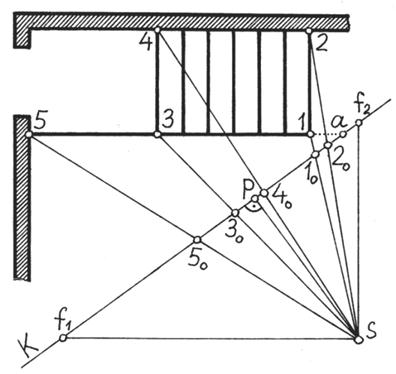
Рисунок 43 – Начальный этап построения перспективы лестницы. План

Построение перспективы лестницы. В качестве примера можно рассмотреть построение перспективы лестницы, расположенной в угловой части помещения (рисунки 43 и 44). В данном случае построение ведется способом архитекторов. Вначале на плане проводятся проецирующие лучи к крайним точкам лестницы, а затем вычерчиваются основные параметры лестницы, которые на перспективном изображении заданы точками 1´, 2´, 3´, 4´, 5´ и 6´ (точка 6´ получена на пересечении прямых 5´- F2 и 4´-F1). Этот этап построения подробно не излагается, поскольку способ архитекторов неоднократно описывался ранее. Можно лишь пояснить, что в данной ситуации построения могут быть выполнены при условии, что известна высота лестницы. Эта высота равна отрезку Аа на перспективном изображении, который следует отложить вверх от точки а, полученной при продлении отрезка 1-5 до пересечения с основанием картинной плоскости.

Рисунок 44 – Завершающий этап построения перспективы лестницы

Затем отрезок Аа делится точками I, II, III, IV, V, VI на семь равных отрезков соответственно количеству ступеней. После этого проводятся прямые I-F1, II-F1, III-F1, IV-F1, V-F1, VI-F1, которые делят отрезок 1´-3´ в точках I´, II´, III´, IV´, V´, VI´. Эти точки являются вершинами углов ступеней. Дальнейшее построение ступеней не составляет труда – горизонтальные ребра ступеней будут идти в точки схода F1 и F2. При этом если мысленно провести отрезок 2´-4´, то дальние от зрителя углы ступеней будут располагаться на этом отрезке.

Дата добавления: 2014-12-27