Построение окружностей и тел вращения в перспективе

Наиболее распространенным способом построения окружности в перспективе является способ описанного квадрата. Этот способ предполагает, что вначале строится перспектива квадрата, в который затем вписывается эллипс. В качестве примера можно рассмотреть процесс построения перспективы горизонтально расположенной окружности, которая вписана в квадрат со сторонами параллельными картинной плоскости (рисунок 33).

Построение квадрата ведется следующим образом. Намечается ближайшая к зрителю сторона квадрата АВ, из вершин которой проводятся прямые в главную точку Р. Уходящие в глубину стороны квадрата АВ и ВС строятся с помо-

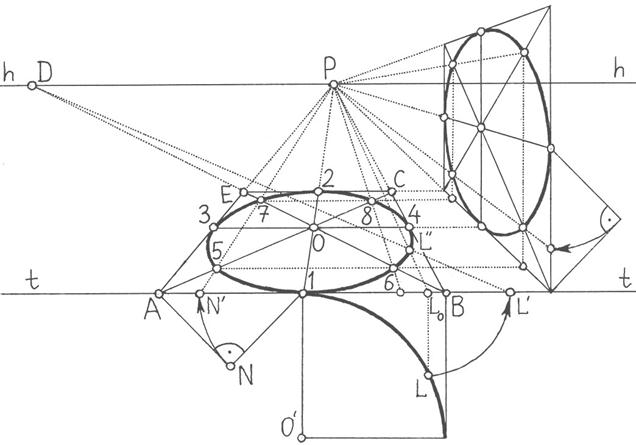
Рисунок 33 - Построение окружности способом описанного квадрата во фронтальной перспективе

щью дистанционной точки D согласно правилам построения масштаба глубины. На пересечении диагоналей квадрата будет располагаться точка О – центр окружности. Через точку О проводятся горизонтальная прямая и прямая ОР. Эти прямые, являясь осями симметрии квадрата и окружности, пересекут стороны квадрата в точках 1, 2, 3 и 4. Данные точки обозначают места касания эллипса к сторонам квадрата.

На диагоналях квадрата можно построить еще четыре точки эллипса. Так, чтобы построить точки 5 и 7, вычерчивается равнобедренный прямоугольный треугольник AN1 и откладывается отрезок N'1, равный меньшей стороне треугольника. Далее проводится прямая N'Р, пересекающая диагонали треугольника в искомых точках 5 и 7. Чтобы построить еще две точки эллипса, проводятся горизонтальные прямые через точки 5 и 7. Места пересечения этих прямых с диагоналями квадрата обозначают расположение данных точек (они обозначены цифрами 6 и 8). На завершающем этапе построения точки эллипса от 1 до 8 соединяются плавными кривыми линиями.

Иногда, для того чтобы добиться большей точности построения, возникает необходимость найти перспективное расположение дополнительных точек окружности. Для этого в нижней части изображения можно вычертить фрагмент окружности во фронтальной плоскости с радиусом, равным половине стороны квадрата АВСЕ. В данном случае это дуга с центром в точке О', касающаяся стороны квадрата в точке 1. На дуге откладывается произвольно взятая точка L. Из этой точки проводится перпендикуляр к стороне квадрата, пересекающий ее в точке L0. Далее на прямой АВ откладывается отрезок L0-L', равный отрезку L0-L. Затем точка L' соединяется с дистанционной точкой D. В месте пересечения прямых L0-Р и L'-D будет располагаться точка L'', которая является одной из точек эллипса. Аналогичным образом можно построить ряд других точек окружности в перспективе.

Стоит заметить, что подобный способ нахождения дополнительных точек окружности пригоден лишь при построении крупных эллипсов. Построение небольших окружностей в перспективе таким способом не имеет смысла, поскольку в этом случае неизбежные графические погрешности приводят к искажению формы.

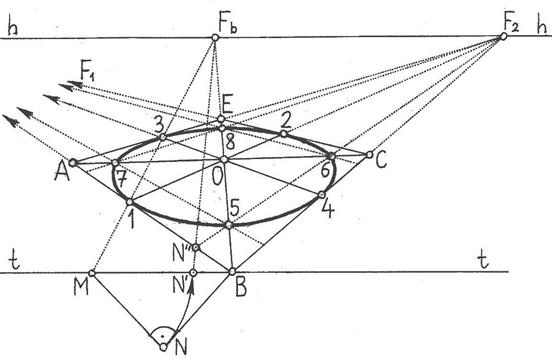
Рисунок 34 - Построение окружности способом описанного квадрата в угловой перспективе

На рисунке 34 показан пример построения окружности, вписанной в квадрат АВСD, расположенный в угловой перспективе и касающийся основания картины (квадрат может быть построен одним из описанных в предыдущем параграфе способов построения перспективы). Сначала проводятся диагонали квадрата и в месте их пересечения определяется точка О – центр будущей окружности, из которой проводятся прямые в точки схода F1 и F2 (точка F1 с целью экономии места не показана). Эти прямые пересекут стороны квадрата в точках 1, 2, 3 и 4. В данных точках окружность касается сторон квадрата.

Далее строятся точки окружности на диагоналях квадрата. Для определения месторасположения точек 5 и 6 вначале из точки Fb, являющейся точкой схода прямой ВЕ, проводится прямая через точку 1 и пересекающая основание картинной плоскости в точке М. Затем строится равнобедренный прямоугольный треугольник МВN и на основании картинной плоскости откладывается отрезок MN', равный MN. Далее проводится прямая N'Fb и в месте пересечения данной прямой со стороной АВ откладывается точка N''. Из этой точки проводится прямая в точку схода F2, в месте пересечения которой с диагоналями квадрата будут располагаться точки 5 и 6. Если через данные точки провести прямые в точку схода F1, то места пересечения этих прямых с диагоналями квадрата будут обозначать положение еще двух точек эллипса, обозначенных цифрами 7 и 8. Получившиеся точки от 1 до 8 аккуратно соединяются кривыми линиями.

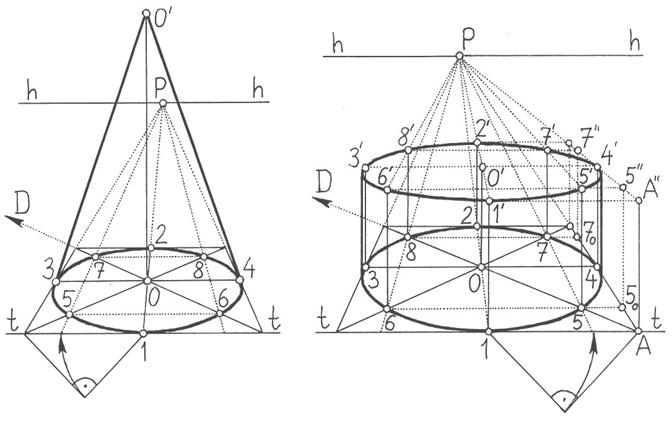
Рисунок 35 - Построение конуса Рисунок 36 - Построение цилиндра в перспективе в перспективе

На рисунках 35 и 36 показано перспективное построение простейших тел вращения – цилиндра и конуса. При построении вертикально расположенного конуса сначала по описанной выше схеме строится перспектива окружности в основании конуса, а затем от центра эллипса вертикально вычерчивается ось конуса ОО' (ее высота находится по правилам построения масштаба высоты), после чего остается соединить вершину конуса по касательной с боковыми краями эллипса. Следует заметить, что, строго говоря, отрезки проведенные из точки О' и обозначающие боковые края конуса, в данном случае касаются эллипса в точках, расположенных немного ближе к зрителю, чем точки 3 и 4. Расположение мест касания зависит от пропорций конуса и местонахождения наблюдателя и обычно определяется «на глаз», если не требуется особая точность построений.

На первом этапе построения вертикально расположенного цилиндра сначала также строится нижний эллипс (рисунок 36). Далее начинается построение верхнего эллипса. Сначала откладывается отрезок 1-1', его высота равна высоте цилиндра в натуральную величину, поскольку сам отрезок лежит в картинной плоскости. Высота отрезков О-О' и 2-2' находится по правилам построения масштаба высоты, а высота отрезков 3-3' и 4-4' откладывается равной высоте О-О'. Далее, как видно на рисунке, от угла описанного вокруг окружности квадрата откладывается отрезок АА'' и проводится прямая А''-Р. На прямой АР откладывается точка 50, полученная путем горизонтального переноса точек 5 и 6, а также точка 70, аналогичным образом полученная путем переноса точек 7 и 8. Затем на прямой АР откладываются точки 5'' и 7'', полученные вертикальным переносом точек 50 и 70. Из точек 5 и 7 проводятся горизонтальные прямые, места пересечения которых с вертикальными отрезками, проведенных из точек 5, 6, 7 и 8, обозначают расположение еще четырех точек верхнего эллипса - 5', 6', 7' и 8'. После этого остается плавно соединить полученные восемь точек верхнего эллипса.

Следует отметить, что ширина эллипсов по горизонтали несколько превышает расстояние между отрезками 3-3' и 4-4' и, соответственно, боковые края цилиндра, как показано на рисунке 36, не совпадают с этими отрезками.

Дата добавления: 2014-12-27