Перспектива точки, прямой и плоскости

Перспектива точки. Перспективное расположение точки в пространстве можно определить, если известны высота точки относительно предметной плоскости и перспективное расположение ее горизонтальной проекции (это расположение, в свою очередь, может быть определено по изображению точки на плане).

Допустим, требуется построить перспективу точки А, расположение которой на плане задано ее горизонтальной проекцией – точкой а (рисунок 4). Для этого сначала из точки s к точке а на плане проводится проецирующий луч, пересекающий картинную плоскость в точке а1. Далее из точки а на плане проводится перпендикуляр к картинной плоскости, пересекающий ее в точке а0. Точки а1 и а0 переносятся на основание картинной плоскости с соблюдением расстояний между ними и точкой р. Затем от точки а0 на основании картинной плоскости проводится вверх перпендикуляр, на котором откладывается точка А0, высота которой соответствует высоте точки А. От точки а1 также проводится перпендикуляр вверх от основания картинной плоскости. Места пересечения этого перпендикуляра с прямыми А0Р и а0Р обозначают искомое перспективное расположение точки А и ее горизонтальной проекции.

Перспектива прямой общего положения. Прямой общего положения называется прямая, расположенная под произвольным углом к картинной и предметной плоскостям. Рассмотрим на рисунке 5 произвольно расположенную прямую АN, пересекающую картинную плоскость в точке N (точка пересечения прямой с картинной плоскостью называется картинным следом прямой). Если провести к любым точкам данной прямой проецирующие лучи, то они пересекут картинную плоскость в соответствующих точках. Так точкам 1, 2, 3 прямой АN соответствуют точки 1', 2', 3' на картинной плоскости. Множество точек 1', 2', 3' и т.д. образует прямую, которая является перспективным изображением прямой АN. Эта прямая, будучи в действительности бесконечной, имеет строго определенный предел на перспективном изображении. Так проецирующий луч SF, параллельный прямой AN, не пересекает ее, то есть точка пересечения этого луча с картинной плоскостью не соответствует ни одной из точек этой прямой. Далее, если в воображаемой плоскости, заключающей в себе точку S и прямую AN, провести бесконечное множество проецирующих лучей, расположенных в данном случае справа от точки F, то они также не будут пересекать эту прямую (например, как видно из рисунка 5, луч SВ не пересекает прямую AN и, соответственно, перспективное изображение прямой не проходит через точку пересечения этого луча с картинной плоскостью). Таким образом, перспектива прямой, изображенной на рисунке, ограничена в пределах между точками N и F. Точку F называют бесконечно удаленной точкой или точкой схода прямой. Перспективное изображение каждой прямой, не параллельной картинной плоскости, имеет точку схода. Точка схода прямой является точкой для всех прямых параллельных данной прямой.

Перспективу всякой прямой можно построить, если известно расположение двух любых ее точек. На рисунке 6 показано построение перспективы прямой общего положения АВ. Как видно из рисунка, точка А является картинным следом данной прямой. Положение прямой на плане задано ее горизонтальной проекцией ab. Точка В и ее горизонтальная проекция строятся в перспективе

Рисунок 5 – Получение перспективного изображения прямой общего положения

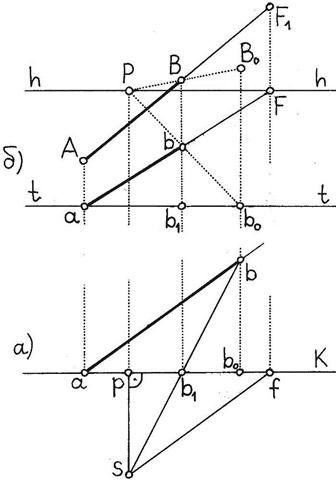аналогично тому, как было построено перспективное изображение точки А и ее горизонтальной проекции на рисунке 4.

Чтобы построить точку схода прямой АВ, следует сначала построить точку схода прямой ab, которая располагается на пересечении ее с линией горизонта (точка F на перспективном изображении). Если из точки F провести перпендикуляр вверх от линии горизонта, то место пересечения этого перпендикуляра с прямой АВ будет обозначать положение точки F1, являющейся точкой схода данной прямой.

На рисунке 7 показано построение перспективы двух параллельных прямых, имеющих общую точку схода.

Перспектива прямых линий частного положения. К прямым частного положения относятся следующие прямые, занимающие определенное положение относительно картинной плоскости:

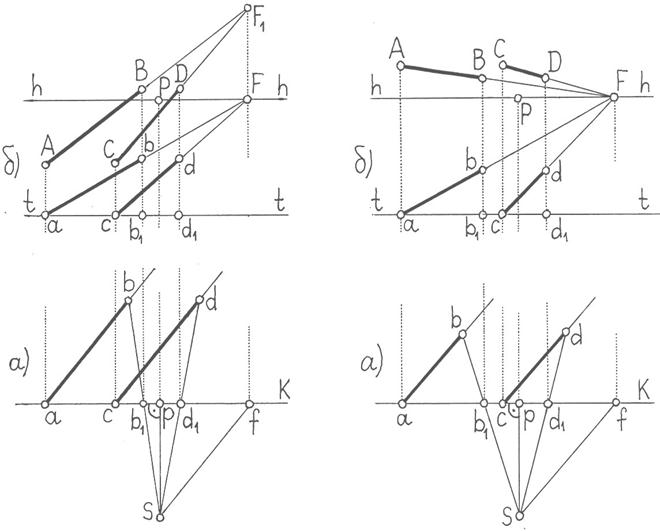
Рисунок 7 – Построение перспективы Рисунок 8 – Построение перспективы параллельных прямых общего параллельных горизонтальных прямых,

положения. а) план, б) перспектива расположенных под произвольным углом к картинной плоскости

1) горизонтальные прямые, наклонные к картинной плоскости. Точка схода параллельных прямых такого рода, как было ранее сказано, лежит на линии горизонта и не совпадает с точкой Р. Пример построения подобных прямых приведен на рисунке 8. Как видно из рисунка, эти прямые строятся по тому же принципу, что и прямые общего положения.

2) горизонтальные прямые, перпендикулярные картинной плоскости. Эти прямые на перспективном изображении сходятся в точку Р (рисунок 9).

3) прямые, параллельные картинной плоскости. Эти прямые, как ясно из определения, не имеют картинных следов и точек схода. Плоские фигуры, ограниченные отрезками такого рода прямых, изображаются в перспективе подобными – в качестве примера показана перспектива треугольника на рисунке 10.

4) прямые, вторичные проекции которых проходят через основание точки зрения, а также прямые, расположенные в предметной плоскости и сходящиеся в

Рисунок 9 – Построение перспективы Рисунок 10 – Построение перспективы прямых, перпендикулярных картине отрезков, параллельных картине

основание точки зрения (эти прямые принято называть радиальными), изображаются в перспективе вертикальными, как показано на рисунке 12.

5) горизонтальные прямые, расположенные под углом 45° к картинной плоскости. Такого рода прямые на перспективном изображении сходятся в дистанционные точки D1 и D2 (рисунок 13).

Перспектива плоскости. Построение перспективы плоскости в данном случае можно рассмотреть на примере плоскости общего положения, под которой понимается плоскость, расположенная под произвольным углом к картинной и предметной плоскостям.

Построить перспективу плоскости возможно при условии, что известно положение хотя бы одной прямой и одной точки, лежащих в пределах данной плоскости. На рисунке 14 показано расположение прямой АF1 и точки В, находящихся в плоскости, которую требуется построить. При этом точка А является картинным следом прямой АF1, а точка F1 ее точкой схода; местонахождение прямой АF1 и точки В задано их вторичными проекциями.

Сначала можно построить прямую, по которой будет пересекаться плоскость с картинной плоскостью (эта прямая называется картинным следом плоскости). Месторасположение одной из точек данной прямой, точки А, известно. Чтобы построить прямую, следует найти положение еще одной ее точки. Для

Рисунок 12 - Построение Рисунок 13 - Построение перспективы перспективы радиальных прямых горизонтальных прямых, расположенных

под углом 45 ° к картинной плоскости

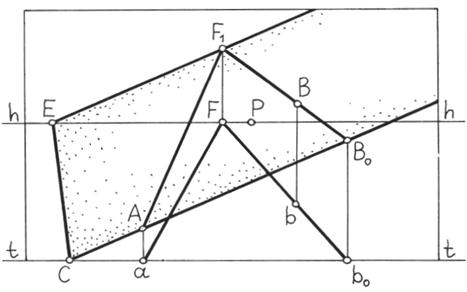
Рисунок 14 – Построение перспективы плоскости ВоСЕF1.

ВоС – картинный след плоскости, ЕF1 - линия схода плоскости, СЕ - горизонтальный след плоскости

этого проводятся прямые ВF1 и bF. От точки bо, в которой пересекаются прямая bF с основанием картинной плоскости, проводится вертикальный луч до пересечения с прямой ВF1 в точке Во, являющейся картинным следом данной прямой. Прямая АВо является картинным следом плоскости, которую требуется построить. Эта прямая пересекается с основанием картины в точке С.

Далее через точку F1 проводится прямая, параллельная АВо. Эта прямая называется прямой схода плоскости (перспективное изображение каждой плоскости имеет бесконечно удаленную прямую или прямую схода, аналогично тому как прямая в перспективе имеет точку схода). Прямая схода всегда параллельна картинному следу плоскости и является прямой схода для всех прямых, параллельных данной плоскости.

Затем точка Е, в которой пересекаются прямая схода плоскости и линия горизонта, соединяется с точкой С. Прямая ЕС является линией пересечения плоскости с предметной плоскостью, эту линию называют горизонтальным следом плоскости. Построенные таким образом картинный след плоскости, линия схода плоскости и ее горизонтальный след определяют искомое перспективное расположение плоскости ВоСЕF1.

Можно еще заметить, что у горизонтальных плоскостей картинный след также расположен горизонтально, а линия схода совпадает с линией горизонта. У вертикально размещенных плоскостей и картинный след, и линия схода расположены вертикально.

Дата добавления: 2014-12-27