Многоканальной СМО с ожиданием

Общие сведения о применении теории массового обслуживания для определения статистических характеристик технического обслуживания

Цель работы

Определение статистических характеристик технического обслуживания замкнутой системы массового обслуживания с ожиданием

Описания и индивидуальные задания лабораторных работ по технической эксплуатации, в которых используется математический аппарат теории массового обслуживания

Содержание отчета

Лабораторное задание

Представленной на рисунке 3.44

Таблица 3.10 – Результаты сравнительных функциональных испытаний стабильности выходного напряжения

Тип усилительного каскада	δ(%/^оС)
Каскад с разомкнутой САУ и с управлением по задающему воздействию (рисунок 3.34)	0.397
Каскад с разомкнутой САУ и с комбинированным управлением по задающему и по возмущающему воздействиям (рисунок 3.36)	0.048
Каскад с замкнутой САУ с комбинированным управлением по задающему и по возмущающему воздействиям (рисунок 3.38)	0.013
Каскад с замкнутой САУ с управлением по задающему воздействию (рисунок 3.40)	0.00035
Каскад с разомкнутой САУ и с управлением по задающему воздействию при подаче на вход каскада синусоидального напряжения (рисунок 3.42)	1.009
Каскад с замкнутой САУ с комбинированным управлением по задающему и по возмущающему воздействиям при подаче на вход каскада синусоидального напряжения (рисунок 3.44)	» 0

Получить у преподавателя номер варианта задания. Провести сравнительные функциональные испытания стабильности выходного напряжения у = U _ВЫХ = U_{R 4} математических моделей усилительных каскадов, изображённых на рисунках 3.34, 3.36, 3.38, 3.40, 3.42, 3.44, при изменении температуры эксплуатации от -40^оС до +60^оС. Для всех вариантов задания принять тип транзистора КТ819А, тип диода КD512А, величину сопротивления R 4 = 100 Ом, величину сопротивления R 5 = 5 Ом, амплитуду переменного напряжения с частотой 900 Гц V 2 = 0.1 В. Величины напряжения питания V 1 и сопротивлений R 1, R 2, R 4 найти в таблице 3.11 для заданного номера варианта. При выполнении задания руководствоваться методикой проведения сравнительных функциональных испытаний стабильности выходного параметра усилительных каскадов, подробно изложенной в пункте 3.4.3.

Таблица 3.11 – Величины напряжения питания V 1и сопротивлений R 1, R 2, R 4 для разных вариантов задания

№ вари- анта	R 2, Омдля рис.3.34, 3.42 и 3.44	R 2, Омдля рис.3.36, 3.38 и 3.40	V 1 , В	R 5 , Ом	R 1 , Ом	№ вари- анта	R 2, Омдля рис.3.34, 3.42 и 3.44	R 2, Омдля рис.3.36, 3.38 и 3.40	V 1 , В	R 5 , Ом	R 1 , Ом
				4.7						5.6
				5.1						6.2
				5.6						6.8
				6.2						7.5
				6.8						4.7
				7.5						5.1
				4.7						5.6
				5.1						6.2
				5.6						6.8
				6.2						7.5
				6.8						4.7
				7.5						5.1

1. Цель работы.

2. Графики, таблицы и расчёты по методике, изложенной в пункте 3.4.3, отображающие результаты сравнительных функциональных испытаний стабильности выходного напряжения у = U _ВЫХ = U_{R 4} при изменении температуры. Математические модели усилительных каскадов подготовить в системе MicroCAP 8. В результате расчётов должны быть решены все вопросы, изложенные в лабораторном задании.

3. Выводы по работе.

3.4.6 Перечень контрольных вопросов, которые могут быть заданы во время защиты отчёта по работе

1. Каковы преимущества методов сравнительных испытаний РЭС при изменении температуры эксплуатации в широком диапазоне на математических моделях в системе MicroCAP 8 перед испытаниями на реальных образцах РЭС?

2. К какому типу САУ относятся усилительные каскады (к линейным или к нелинейным):

а) по отношению к регулирующему воздействию;

б) по отношению возмущающего воздействия температуры эксплуатации?

3. Чем отличаются разомкнутые САУ от замкнутых?

4. Чем отличаются САУ:

а) с управлением по задающему воздействию;

б) с управлением по возмущающему воздействию;

в) с комбинированным управлением по задающему и по возмущающему воздействиям?

5. Каково главное достоинство замкнутой системы регулирования?

6. Каков порядок величины температурного дрейфа у каскада с разомкнутой САУ и с управлением по задающему воздействию, и каков у каскада с комбинированным управлением по задающему и по возмущающему воздействиям?

Обучить студентов применению методики по определению статистических характеристик технического обслуживания применительно к замкнутой системе массового обслуживания с ожиданием. Методика базируется на использовании программного комплекса MathCAD.

Теория массового обслуживания (ТМО) изучает статистические характеристики систем массового обслуживания. Система массового обслуживания (СМО) – это совокупность однородных обслуживающих устройств (приборов, мастерских и т.д.), называемых каналами обслуживания. Примерами СМО могут служить сборочные цеха, ремонтные мастерские, инженерно-авиационная служба, восстанавливаемая резервированная аппаратура, телефонные станции, все виды транспорта (вместе с билетными кассами) и т.д.

Основными элементами СМО, определяющими их пропускную способность, являются: число каналов обслуживания, быстродействие каждого канала и поток событий (заявок на обслуживание, поток обслуженных заявок и т.д.).

По признаку потерь заявок на обслуживание СМО подразделяются на три типа: с отказами, с ожиданием и смешанного типа.

В СМО с отказами заявки обслуживаются немедленно, если каналы свободны, или получают отказ и теряются, если все каналы заняты. Пример такой СМО – телефонная сеть. В СМО с ожиданием (например, в системах ремонта техники) все заявки выстраиваются в очередь, если каналы заняты. В СМО смешанного типа имеются ограничения на время пребывания заявки в системе или на длину очереди. При невыполнении требуемого ограничения заявка покидает СМО необслуженной.

По числу каналов обслуживания, которые могут одновременно обслуживать входные заявки, СМО делят на одноканальные и многоканальные.

Если обслуженная заявка покидает СМО, то СМО называют открытыми, а если снова поступает на обслуживание в СМО, то замкнутыми.

При выполнении лабораторной работы мы исследуем замкнутую многоканальную СМО с ожиданием, наиболее подходящую для описания процесса эксплуатации техники, в частности, для расчета характеристик ТО и показателей надежности резервируемой аппаратуры в зависимости от числа каналов и их производительности.

Пусть СМО с ожиданием содержит n работающих приборов и r каналов обслуживания. При одном отказе прибора получается одна заявка. Поток отказов порождает поток заявок, которые немедленно удовлетворяются обслуживанием, а когда все r каналов обслуживания заняты, заявки выстраиваются в очередь. В этом случае r ≤ k < n, где k – число отказов приборов. Требуется найти вероятности пребывания системы в состоянии Р_k (t) в любой момент времени t для различных значений k. Вероятность Р_k (t)− это вероятность состояния системы, при котором k приборов отказали, из них r приборов обслуживаются, а остальные (k – r) стоят в очереди. Найденные значения Р_k (t) позволяют рассчитать все критерии, характеризующие степень удовлетворения потока заявок и степень использования каналов обслуживания. Предполагается, что вероятность безотказной работы любого прибора изменяется во времени по экспоненциальному закону P (t) = exp(–λ t), причём интенсивность отказов (поступления заявок) λ не зависит от времени. Если до момента t прибор был исправен, то вероятность отказа Р _ОТК(∆ t) в малом промежутке времени ∆t, следующем за временем t, для нашего случая определяется приближенным выражением:

Р _ОТК(∆ t)» lD t, при lD t << 1. (4.1)

По аналогии определяется вероятность завершения обслуживания заявки к моменту t + ∆ t, поступившей в момент t на обслуживание:

Р _ОБС(∆ t)» μ∆ t, при μ∆ t << 1. (4.2)

В (4.2) μ− это интенсивность восстановления (обслуживания, ремонта) в одном канале. Граф изменения состояний замкнутой многоканальной СМО с ожиданием представлен на рисунке 4.1.

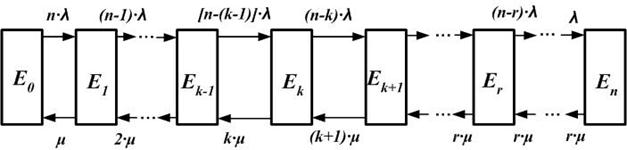
Рисунок 4.1 – Граф изменения состояний замкнутой

Под термином техническоесостояние Е_k понимают совокупность подверженных изменению в процессе производства или эксплуатации свойств объекта, характеризуемую в определённый момент признаками, установленными технической документацией.

На рисунке 4.1 введены следующие обозначения:

- Е_k – техническоесостояние СМО, при котором k из n работающих приборов находятся в состоянии неработоспособности;

- r − число каналов обслуживания;

- λ [ч^-1] − интенсивность поступления заявок, равная интенсивности отказов одного прибора;

- μ [ч^-1] − интенсивность обслуживания (восстановления или ремонта) в одном канале.

Указанная СМО может использоваться как система технического обслуживания не только приборов, но и транспорта (парки самолетов, автомобилей и т.п.).

Академик А.Н.Колмогоров сформулировал инженерное правило составления дифференциальных уравнений по виду графа или по виду схемы состояний [1, 4]:

«Производная от вероятности пребывания системы в любой момент времени в состоянии k равна алгебраической сумме произведений интенсивностей переходов в k -ое состояние (или из k -ого состояния) на вероятность того состояния, откуда совершается переход в k- ое состояние. Причем, тем слагаемым, которым соответствуют уходящие стрелки из k -ого состояния, приписывается знак «минус», а входящим – «плюс».

Анализ графа (рисунок 4.1) позволяет вывести дифференциальное уравнение для вероятностей состояний:

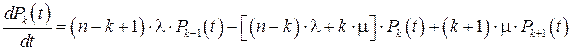. (4.3)

Для установившегося режима 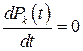, так как P_k в этом случае не меняется во времени, и уравнение для вероятности состояний примет вид:

(n – k + 1)×λ× P_{k -1} + [(n – k)×λ + k ×μ]× P_k + (k + 1)×μ× P_{k +1} = 0. (4.4)

Решение уравнения для вероятностей в этом случае дает результат:

P_k = A_k × P ₀, (4.5)

где P ₀ − вероятность того, что работают все приборы.

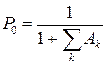; (4.6)

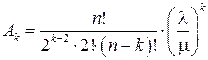. (4.7)

Для проверки правильности расчета P_k используется нормировочное отношение:

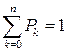. (4.8)

Суммарная погрешность расчета P_k находится из выражения:

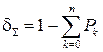. (4.9)

Полученные выражения для P_k (вероятностей пребывание системы в состоянии k) позволяют с помощью схемы для определения статических характеристик СМО, изображенной на рисунке 4.2, определять эти характеристики [1]:

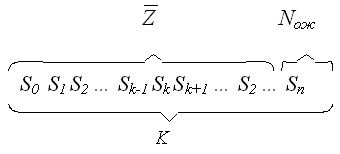
Рисунок 4.2 – Схема определения статических характеристик СМО

а) среднее количество заявок в каналах обслуживания, то есть среднее количество каналов занятых на ремонте:

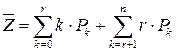, (4.10)

где первое слагаемое характеризует отсутствие очереди, а второе – очередь;

б) пропускная способность:

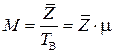, (4.11)

где Т _В− среднее время восстановления одного прибора, величина обратная интенсивности восстановления;

в) среднее число заявок, находящихся в СМО (как в каналах обслуживания, так и в очереди на обслуживание):

; (4.12)

г) среднее число заявок, находящихся в очереди на обслуживание:

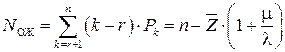; (4.13)

д) среднее число простаивающих каналов обслуживания из-за отсутствия заявок:

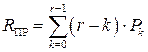; (4.14)

е) среднее относительное время простоя каждого канала СМО из-за отсутствия заявок:

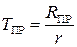при r > 1; (4.15)

ж) среднее относительное значение времени пребывания заявок в очереди на обслуживание:

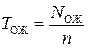; (4.16)

з) среднее относительное значение времени пребывание заявок в очереди и в канале обслуживания:

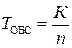; (4.17)

и) при определении минимального количества каналов обслуживания r _min, обеспечивающего отсутствие очереди на обслуживание, используют неравенство:

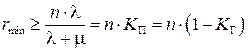, (4.18)

где К _П и К _Г – коэффициенты простоя и готовности, соответственно.

Дата добавления: 2014-12-27