Этапы выполнения лабораторной работы. Индивидуальные задания для расчета в лабораторной работе характеристик технического обслуживания замкнутой многоканальной СМО с ожиданием

Индивидуальные задания для расчета в лабораторной работе характеристик технического обслуживания замкнутой многоканальной СМО с ожиданием

Пример использования ТМО для расчета характеристик технического обслуживания замкнутой многоканальной СМО с ожиданием

Дана СМО, состоящая из n = 9 работающих приборов и r = 3 каналов обслуживания. Интенсивность поступления заявок, равная интенсивности отказов одного прибора, λ = 0.1671 [ч^-1], а интенсивность обслуживания (восстановления или ремонта) в одном канале μ = 0.3 [ч^-1]. Требуется определить:

а) среднее количество заявок 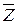, занятых в каналах обслуживания, то есть занятых каналов на ремонте;

б) пропускную способность M;

в) среднее число заявок K, находящихся в СМО (как в каналах обслуживания, так и стоящих в очереди на обслуживание);

г) среднее число заявок N _ОЖ, находящихся в очереди на обслуживание;

д) среднее число простаивающих каналов обслуживания из-за отсутствия заявок R _ПР;

е) среднее относительное время простоя каждого канала обслуживания из-за отсутствия заявок Т _ПР;

ж) среднее относительное значение времени пребывания заявки в очереди на обслуживание Т _ОЖ;

з) среднее относительное значение времени пребывания заявки в очереди и в канале обслуживания Т _ОБС;

и) потребное количество каналов, обеспечивающее отсутствие очереди r _ОПТ.

Решение:

а) находим вспомогательные коэффициенты А_к при 1 £ k £ n:

;

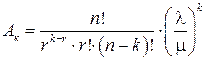А ₁ = 7.52; А ₂ = 11.169; А ₃ = 14.516; А ₄ = 16.171;

А ₅ = 15.012; А ₆ = 11.149; А ₇ = 6.21; А ₈ = 2.306; А ₉ = 0.428;

б) определим вспомогательную величину Р ₀ (вероятность того, что в системе исправно работают все приборы):

;

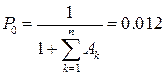в) находим вероятность нахождения системы в k -ом состоянии, т.е. в состоянии, когда k приборов отказали (1 £ k £ n):

P_k = A_k × P ₀;

P ₁ = 0.088; P ₂ = 0.131; P ₃ = 0.17; P ₄ = 0.189;

P ₅ = 0.176; P ₆ = 0.13; P ₇ = 0.073; P ₈ = 0.027; P ₉ = 5.009·10^-3.

Проверка правильности решения:

;

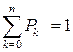г) находим среднее количество заявок в каналах обслуживания:

; ;

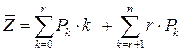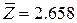д) находим пропускную способность M:

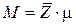; M = 0.797;

е) находим среднее количество заявок находящихся в СМО (в каналах и в очереди):

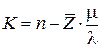; K = 4.227;

ж) находим среднее количество заявок, находящихся в очереди на обслуживание:

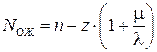; N _ОЖ = 1.569;

з) находим среднее количество простаивающих каналов из-за отсутствия заявок:

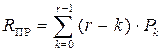; R _ПР = 0.343;

и) находим среднее относительное время простоя из-за отсутствия заявок:

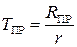; Т _ПР = 0.114;

к) находим среднее относительное значение времени пребывания заявки в очереди:

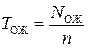; Т _ОЖ = 0.174;

л) находим среднее относительное значение времени пребывания заявки в СМО:

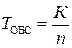; Т _ОБС = 0.47;

м) определяем коэффициент готовности:

; К _Г = 0.642;

н) находим потребное количество каналов, необходимых для обеспечения отсутствия очереди:

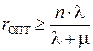; r _ОПТ ³ 3.22.

Принимаем r _ОПТ= 4, то есть равным ближайшему целому числу большему 3.22.

Дана СМО, состоящая из n работающих приборов и r каналов обслуживания. Интенсивность поступления заявок (интенсивность отказов одного прибора) равна λ, а интенсивность обслуживания (восстановления или ремонта) в одном канале равна μ.

Определить:

а) среднее количество заявок 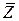, занятых в каналах обслуживания, то есть занятых каналов на ремонте;

б) пропускную способность M;

в) среднее число заявок K, находящихся в СМО (как в каналах обслуживания, так и стоящих в очереди на обслуживание);

г) среднее число заявок N _ОЖ, находящихся в очереди на обслуживание;

д) среднее число простаивающих каналов обслуживания из-за отсутствия заявок R _ПР;

е) среднее относительное время простоя каждого канала обслуживания из-за отсутствия заявок Т _ПР;

ж) среднее относительное значение времени пребывания заявки в очереди на обслуживание Т _ОЖ;

з) среднее относительное значение времени пребывания заявки в очереди и в канале обслуживания Т _ОБС;

и) потребное количество каналов, обеспечивающее отсутствие очереди r _ОПТ.

Численные значения исходных величин для расчёта индивидуальных заданий даны в таблице 4.1 и зависит от номера варианта.

Таблица 4.1 – Численные значения исходных величин для расчёта индивидуальных заданий с использованием программного комплекса MathCAD

Первая цифра номера варианта
n
r
Вторая цифра номера варианта
μ, [ч^-^1]		0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0.6
Третья цифра номера варианта
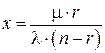
Выражение для определения λ:	0.5	0.55	0.6	0.65	0.7	0.75	0.8	0.85	0.9	0.75

1. Подготовиться к ответу на контрольные вопросы и получить у преподавателя допуск к выполнению задания.

2. Используя номер варианта задания, выданный преподавателем, выполнить расчет задания по пункту 4.1.4.

Дата добавления: 2014-12-27