Общие сведения об открытой многоканальной СМО смешанного типа с ограниченным временем ожидания

Для такой СМО заявки на обслуживание, поступающие на вход системы и заставшие все каналы обслуживания занятыми, встают в очередь. По количеству мест очередь не имеет ограничений. Но заявка, простоявшая некоторое время в очереди и не получившая обслуживание, покидает очередь с интенсивностью ухода ν. Время ожидания распределено экспоненциально со средним сроком ожидания:

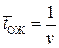.(4.31)

При ν → ∞ многоканальная СМО смешанного типа, с ограниченным временем ожидания, с числом каналов обслуживания s переходит в многоканальную СМО с отказами, а при ν → 0 – в многоканальную чистую СМО с ожиданием. Это позволяет использовать приведённые в данном разделе формулы для СМО смешанного типа при расчёте других СМО указанных выше типов, в зависимости от численного значения ν.

Расчёт проводим по методике, изложенной в пункте 4.2.3 для открытой одноканальной СМО с ожиданием. По инженерному правилу А.Н.Колмогорова по виду графа состояний, изображённого на рисунке 4.5 в виде схемы гибели и размножения, составим систему дифференциальных уравнений. Для стационарного режима система этих дифференциальных уравнений преобразуется в систему линейных уравнений из-за того, что 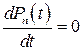. Из линейных уравнений методом подстановки, учитывая, что 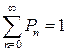получим выражения для вероятностей P_п состояний п [28]:

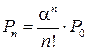; 0 £ n £ s;(4.32)

; s £ n;(4.33)

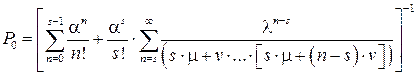.(4.34)

Непосредственное пользование формулой (4.34) затруднено тем, что в неё входит бесконечная сумма. Однако члены этой суммы быстро убывают [32]. При приближенном вычислении вероятности Р ₀ простоя СМО из-за отсутствия заявок на обслуживание в сумме 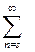формулы (4.34) достаточно ограничиться первыми десятью членами. Здесь стационарный режим существует всегда: ряд Р_п при s < п сходится. Приведём статистические характеристики многоканальной СМО смешанного типа с ограниченным временем ожидания [28].

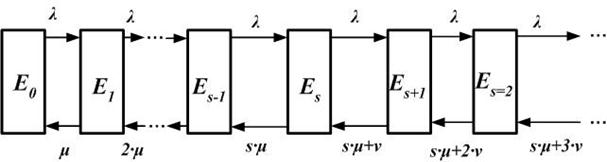
Рисунок 4.5 – Граф переходов многоканальной СМО смешанного типа с ограниченным временем ожидания, изображённый в виде схемы гибели и размножения

Вероятность отказа для данной системы не имеет смысла.

Среднее число заявок N _ОЖ, находящихся в очереди на обслуживание:

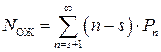. (4.35)

В сумме 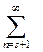формулы (4.35) также достаточно ограничится первыми десятью членами.

Абсолютная пропускная способность:

M = l - v × N _ОЖ, (4.36)

где v × N _ОЖ – заявки, ушедшие из очереди в единицу времени.

Относительная пропускная способность:

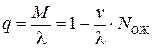. (4.37)

Среднее число 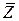занятых каналов:

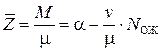.(4.38)

Дата добавления: 2014-12-27