Взяв полную производную по времени, получаем

Основные уравнения газовой динамики выводятся из законов сохранения массы, количества движения и энергии.

Законы сохранения в теории взрыва. Уравнения газовой динамики

Рассмотрим закон сохранения массы. Пусть в момент времени имеется бесконечно малый объем 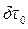. Поскольку при движении газа количество вещества должно оставаться неизменным, то

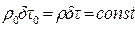, (4.1)

где 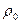и 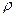- плотность газа для моментов времени 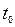и .

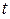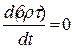
или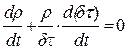

Величина 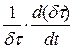представляет собой скорость относительного объемного расширения газа и равна расхождению (дивергенции) скорости в рассматриваемой точке. Следовательно, .

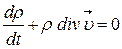Так как 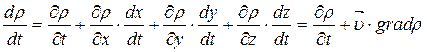, данное уравнение (используя соотношение векторного анализа 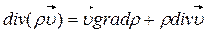), можно представить в виде

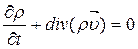(4.2)

Уравнение (4.2) называется уравнением неразрывности.

Рассмотрим уравнение, характеризующее закон сохранения количества движения. По аналогии с выводом уравнения неразрывности выделим некоторый элементарный объем (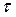). Со стороны газа на этот объем по его поверхности (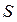) действует давление 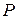. Сила, действующая на поверхность (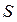), определяется интегралом 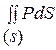. Преобразуя поверхностный интеграл в объемный, находим

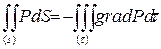
Кроме поверхностных сил, на объем (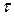) в общем случае могут действовать массовые силы (например, сила тяжести и др.). Пусть 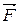- массовая сила, отнесенная к единице массы. Тогда на выделенный объем действует массовая сила 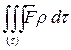. Согласно принципу Даламбера в любой момент времени все силы, действующие на массу 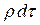, включая силы инерции 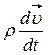, должны находиться в равновесии.

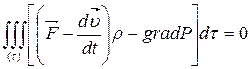(4.3)

Вследствие произвольности объема (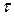) интеграл (4.3) равен нулю, если равно нулю подинтегральное выражение

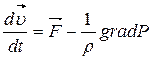
В предыдущем параграфе отмечалось, что во многих задачах, связанных со взрывом, массовой силой 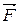можно пренебречь.

Производная 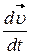может быть представлена как сумма производной скорости по времени 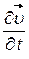и так называемой конвективной производной 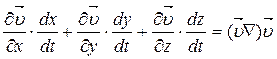, характеризующей изменение скорости в связи с переходом рассматриваемой частицы из одной точки пространства в другую.

Таким образом

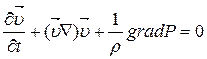(4.4)

Уравнение (4.4) – уравнение движения, известное как уравнение Эйлера.

Рассмотрим уравнение, характеризующее закон сохранения энергии. При выводе этого уравнения целесообразно опираться на 1-ый закон термодинамики

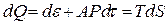, (4.5)

где 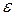- внутренняя энергия, 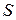- энтропия, 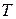- температура.

Или в дифференциальной форме

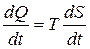
Для адиабатического процесса (с учетом допущения о пренебрежении силами вязкости) 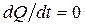, следовательно, 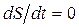. Поскольку 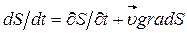, искомое уравнение энергии имеет вид

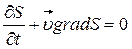(4.6)

Дополнив (4.2), (4.4), (4.6) уравнением состояния

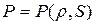, (4.7)

приходят к замкнутой системе уравнений для определения скорости, давления, плотности и энтропии, характеризующих при заданных начальных и граничных условиях состояния газа, как функцию координат и времени.

Для определения температуры среды необходимо знать уравнение состояния в виде 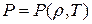или .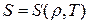

В прямоугольной системе координат уравнения газовой динамики принимают вид:

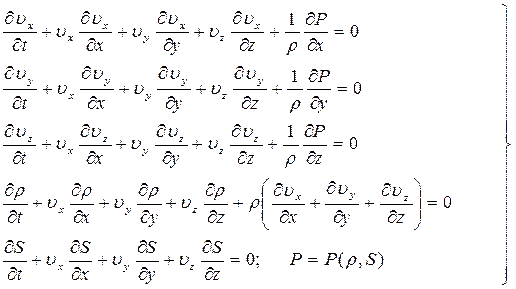(4.8)

Здесь первые три уравнения – это уравнения движения, четвертое – уравнение неразрывности, пятое и шестое – уравнение энергии и уравнение состояния соответственно.

Как отмечалось в § 4.1, решение системы уравнений (4.8) встречает большие математические трудности.

В случае одномерного адиабатического движения идеального газа, т. е., когда все параметры среды зависят от одной геометрической координаты и времени, а уравнение состояния имеет вид (1.6) или (1.13), т. е. 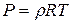или 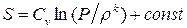, система уравнений газовой динамики упрощается:

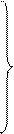
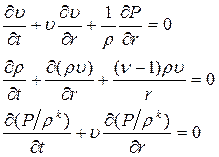(4.9)

где 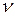=1,2,3 для движений с плоской, цилиндрической и сферической симметрией соответственно.

Системой уравнений (4.9) пользуются при решении целого ряда задач, связанных со взрывами.

Дата добавления: 2014-12-27